文章目录
- 2数字图像基础
- 2.4图像取样和量化
- 2.4.4图像内插
- 2.5像素间的一些基本关系
- 2.5.1相邻像素
- 2.5.2邻接性、连通性、区域和边界
- 2.5.3距离度量
- 2.6 数字图像处理
- 2.6.1阵列和矩阵操作
- 2.6.2线性操作和非线性操作
- 2.6.3算术操作
- 2.6.5空间操作
- 2.6.6向量与矩阵操作
- 2.6.7图像变换
- 2.6.8概率方法
2数字图像基础
2.4图像取样和量化
2.4.4图像内插
内插是在诸如放大、收缩、旋转和几何校正制圭务中广泛应用的本工具。
最近邻内差法。我们用一个简单的例子开始讨论该话题 假设一幅大小为 500x500像素的图像要放大 1.5 倍到750x750 像素。一种简单的放大方法是创建一个假想的750x750 网格,它与原始图像有相同的间隔,然后将其收缩,使它准确地与原图像匹配。 显然,收缩后的750x 750 网格的像素间隔要小于原图像的像素间隔。为了对覆盖的每一个点赋以灰度值,我们在原图像中找最接近的像素,并把该像素的灰度赋给750x750网格中的新像素。当我们完成对网格中覆盖的所有点的灰度赋值后,就把图像扩展到原来规定的大小,得到放大后的图像。
# 预处理显示
import cv2
import numpy as np
import matplotlib.pyplot as plt
def cv2_show(*args):
for ttt in range(len(args)):
img=args[ttt]
cv2.imshow('img', img)
cv2.waitKey(0)
cv2.destroyAllWindows()
def plt_show(*args):
for ttt in range(len(args)):
img = args[ttt]
if (len(img.shape) == 3):
img = cv2.cvtColor(img, cv2.COLOR_RGB2BGR)
elif (len(img.shape) == 2):
img = cv2.cvtColor(img, cv2.COLOR_GRAY2RGB)
plt.subplot(231+ttt), plt.imshow(img)
最近邻内差法:
img = cv2.imread('lena.jpg')
print(img.shape) # (263, 263, 3)
img = np.array(img)
img2 = np.zeros([1052, 1052, 3], dtype=np.uint8)
print(img2.shape)#(1052, 1052, 3)
for i in range(len(img2)):
for j in range(len(img2[i])):
for k in range(len(img2[i][j])):
img2[i][j][k] = (img[int(i/4)][int(j/4)][k])
cv2.imwrite('lena2.jpg',img2)
原图和放大图(有些失真):


双线性内插 v ( x , y ) = a x + b y + c x y + d v(x,y)=ax+by+cxy+d v(x,y)=ax+by+cxy+d ,见2.6.5空间操作的图像配准
双三次内插 v ( x , y ) = ∑ i = 0 3 ∑ j = 0 3 a i j x i y j \displaystyle v(x,y)=\sum_{i=0}^3\sum_{j=0}^3a_{ij}x^i y^j v(x,y)=i=0∑3j=0∑3aijxiyj (为商业图像编辑程序标准内插法)
2.5像素间的一些基本关系
2.5.1相邻像素
上下左右这组像素,称之为4邻域
N
4
(
p
)
N_4(p)
N4(p)
四个对角相邻像素,
N
D
(
p
)
N_D(p)
ND(p)
N
4
(
p
)
N_4(p)
N4(p)+
N
D
(
p
)
N_D(p)
ND(p),称之为8邻域
N
8
(
p
)
N_8(p)
N8(p)
2.5.2邻接性、连通性、区域和边界
令V是用于定义邻接性的灰度值集合
(a)4邻接。如果q在集合
N
4
(
p
)
N_4(p)
N4(p)中,则具有V中数值的两个像素p和q是4邻接的。
(b)8邻接。如果q在集合
N
8
(
p
)
N_8(p)
N8(p)中,则具有V中数值的两个像素p和q是8邻接的。
©m邻接(混合邻接)。如果(i)q在
N
4
(
p
)
N_4(p)
N4(p)中,或(ii)q在
N
D
(
p
)
N_D(p)
ND(p)中,且集合
N
4
(
p
)
、
N
D
(
p
)
N_4(p)、N_D(p)
N4(p)、ND(p)中没有来自V中数值的像素,则具有V中数值的两个像素p和q是m邻接的。
假设p ( x 0 , y 0 ) (x_0,y_0) (x0,y0)到q ( x n , y n ) (x_n,y_n) (xn,yn)的路径是 ( x 0 , y 0 ) (x_0,y_0) (x0,y0)、 ( x 1 , y 1 ) (x_1,y_1) (x1,y1)… ( x n , y n ) (x_n,y_n) (xn,yn),称之为通路,其长度为 n n n。
像素集S的全部像素存在一个通路,则称像素p和q在S中连通。对于S中的像素p,S中连通到p的所有像素为S的连通分量。如果S仅有一个连通分量,则称之为连通集。
如果R是连通集(像素子集),则称R为区域。
如果两个区域
R
i
R_i
Ri和
R
j
R_j
Rj临界,则称之它们为邻接区域,反之则不连接区域。
假设一幅图有K个不连接区域(R_1,R_2,…,R_k),且不接触图像边缘。 R u R_u Ru为其并集, ( R u ) C (R_u)^C (Ru)C为并集的补集,则 R u R_u Ru的点为图像的前景, ( R u ) C (R_u)^C (Ru)C的点为图像的背景。
2.5.3距离度量
设 p ( x , y ) , q ( s , t ) , z ( v , w ) p(x,y),q(s,t),z(v,w) p(x,y),q(s,t),z(v,w)
欧氏距离 D e ( p , q ) = [ ( x − s ) 2 + ( y − t ) 2 ] 1 2 D_{e}(p,q) =\left[(x-s)^{2}+(y-t)^{2}\right]^{\frac12} De(p,q)=[(x−s)2+(y−t)2]21
城市街区距离 D 4 ( p , q ) = ∣ x − s ∣ + ∣ y − t ∣ D_4(p,q)=\left|x-s\right|+\left|y-t\right| D4(p,q)=∣x−s∣+∣y−t∣
棋盘距离 D 8 ( p , q ) = max ( ∣ x − s ∣ , ∣ y − t ∣ ) D_8(p,q)=\max(|x-s|,| y-t|) D8(p,q)=max(∣x−s∣,∣y−t∣)
2.6 数字图像处理
2.6.1阵列和矩阵操作
假设两个图像 [ a 11 a 12 a 21 a 22 ] {\begin{bmatrix}a_{11}&&a_{12}\\ {a_{21}}&&a_{22}\end{bmatrix}} [a11a21a12a22]和 [ b 11 b 12 b 21 b 22 ] {\begin{bmatrix}b_{11}&&b_{12}\\ {b_{21}}&&b_{22}\end{bmatrix}} [b11b21b12b22]
阵列相乘: [ a 11 a 12 a 21 a 22 ] [ b 11 b 12 b 21 b 22 ] = [ a 11 b 11 a 12 b 12 a 21 b 21 a 22 b 22 ] \begin{bmatrix}a_{11}&&a_{12}\\ a_{21}&&a_{22}\end{bmatrix}\begin{bmatrix}b_{11}&&b_{12}\\ b_{21}&&b_{22}\end{bmatrix}=\begin{bmatrix}a_{11}b_{11}&&a_{12}b_{12}\\ a_{21}b_{21}&&a_{22}b_{22}\end{bmatrix} [a11a21a12a22][b11b21b12b22]=[a11b11a21b21a12b12a22b22]
矩阵相乘: [ a 11 a 12 a 21 a 22 ] [ b 11 b 12 b 21 b 22 ] = [ a 11 b 11 + a 12 b 21 a 11 b 12 + a 12 b 22 a 21 b 11 + a 22 b 21 a 21 b 12 + a 22 b 22 ] \begin{bmatrix}a_{11}&&a_{12}\\ a_{21}&&a_{22}\end{bmatrix}\begin{bmatrix}b_{11}&&b_{12}\\ b_{21}&&b_{22}\end{bmatrix}=\begin{bmatrix}a_{11}b_{11}+a_{12}b_{21}&&a_{11}b_{12}+a_{12}b_{22}\\ a_{21}b_{11}+a_{22}b_{21}&&a_{21}b_{12}+a_{22}b_{22}\end{bmatrix} [a11a21a12a22][b11b21b12b22]=[a11b11+a12b21a21b11+a22b21a11b12+a12b22a21b12+a22b22]
2.6.2线性操作和非线性操作
输入
f
(
x
,
y
)
f(x,y)
f(x,y),输出
g
(
x
,
y
)
g(x,y)
g(x,y):
H
[
f
(
x
,
y
)
]
=
g
(
x
,
y
)
H\begin{bmatrix}f(x,y)\end{bmatrix}=g(x,y)
H[f(x,y)]=g(x,y)。
如果
H
[
a
i
f
i
(
x
,
y
)
+
a
j
f
j
(
x
,
y
)
]
=
a
i
H
[
f
i
(
x
,
y
)
]
+
a
j
H
[
f
j
(
x
,
y
)
]
=
a
i
g
i
(
x
,
y
)
+
a
j
g
j
(
x
,
y
)
H\Big[a_i f_i(x,y)+a_j f_j(x,y)\Big]=a_i H\Big[f_i(x,y)\Big]+a_j H\Big[f_j(x,y)\Big]=a_i g_i(x,y)+a_j g_j(x,y)
H[aifi(x,y)+ajfj(x,y)]=aiH[fi(x,y)]+ajH[fj(x,y)]=aigi(x,y)+ajgj(x,y),则其为线性。含有两个特性:加性和同质性。
非线性:如最大值操作。
2.6.3算术操作
四种算术操作: s ( x , y ) = f ( x , y ) + g ( x , y ) d ( x , y ) = f ( x , y ) − g ( x , y ) p ( x , y ) = f ( x , y ) × g ( x , y ) v ( x , y ) = f ( x , y ) ÷ g ( x , y ) \begin{gathered} s(x,y)=f(x,y)+g(x,y) \\ d(x,y)=f(x,y)-g(x,y) \\ p(x,y)=f(x,y)\times g(x,y) \\ v(x,y)=f(x,y)\div g(x,y) \end{gathered} s(x,y)=f(x,y)+g(x,y)d(x,y)=f(x,y)−g(x,y)p(x,y)=f(x,y)×g(x,y)v(x,y)=f(x,y)÷g(x,y)
例2.5针对降噪的带噪图像相加(平均)
令
g
(
x
,
y
)
g(x,y)
g(x,y) 是图像
f
(
x
,
y
)
f(x,y)
f(x,y) 被
η
(
x
,
y
)
\eta(x,y)
η(x,y) 污染后的图像,即
g
(
x
,
y
)
=
f
(
x
,
y
)
+
η
(
x
,
y
)
g(x,y)=f(x,y)+\eta(x,y)
g(x,y)=f(x,y)+η(x,y) 假设噪声不相关,其均值为零,有K幅图像。
则
g
‾
(
x
,
y
)
=
1
K
∑
i
=
1
K
g
i
(
x
,
y
)
\overline{g}(x,y) =\frac{1}{K}\sum_{i=1}^{K}g_{i}(x,y)
g(x,y)=K1i=1∑Kgi(x,y)
E
{
g
‾
(
x
,
y
)
}
=
f
(
x
,
y
)
E{\big\{}{\overline{{g}}}(x,y){\big\}}=f(x,y)
E{g(x,y)}=f(x,y)
σ
g
ˉ
(
x
,
y
)
2
=
1
K
σ
g
(
x
,
y
)
2
=
1
K
σ
η
(
x
,
y
)
2
\sigma_{\bar{g}(x,y)}^{2}=\frac{1}{K}\sigma_{g(x,y)}^{2}=\frac{1}{K}\sigma_{\eta(x,y)}^{2}
σgˉ(x,y)2=K1σg(x,y)2=K1ση(x,y)2 即
σ
g
‾
(
x
,
y
)
=
1
K
σ
η
(
x
,
y
)
\sigma_{\overline{g}(x,y)}=\frac{1}{\sqrt{K}}\sigma_{\eta(x,y)}
σg(x,y)=K1ση(x,y)随着K增大,
E
{
g
ˉ
(
x
,
y
)
}
=
f
(
x
,
y
)
E\{\bar{g}(x,y)\}=f(x,y)
E{gˉ(x,y)}=f(x,y)
例2.6增强差别的图像相减
g ( x , y ) = f ( x , y ) − h ( x , y ) g(x,y)=f(x,y)-h(x,y) g(x,y)=f(x,y)−h(x,y)
例2.7 使用图像相乘相除来校正阴影
- 相乘
- f m = f − min ( f ) f_m=f-\min(f) fm=f−min(f)
- f s = K × f m max ( f m ) f_s=K \times \cfrac{f_m}{\max(f_m)} fs=K×max(fm)fm 映射到[0,K]
img = cv2.imread('tooth.png', 0)
img2 = cv2.imread('ROI.png', 0)
new_img = np.zeros([291, 407])
for i in range(len(img2)):
for j in range(len(img2[i])):
new_img[i][j] = 1.0*img[i][j]*img2[i][j] # 1: multiply
min_f = min([min(v) for v in new_img])
for i in range(len(new_img)):
for j in range(len(new_img)):
new_img[i][j] -= min_f # 2: f_m=f-f_min
max_f = max([max(v) for v in new_img])
for i in range(len(new_img)):
for j in range(len(new_img[i])):
new_img[i][j] = int(255*(new_img[i][j]/max_f)) # 3: f_s=k*f_m/f_max
new_img = new_img.astype(np.uint8)
cv2.imwrite(img=new_img, filename='ans.png')
plt_show(img, img2, new_img)

2.6.5空间操作
几何空间变换
仿射变换 变换名称 仿射矩阵 坐标公式 恒等变换 [ 1 0 0 0 1 0 0 0 1 ] x = v y = w 尺度变换 [ c x 0 0 0 c y 0 0 0 1 ] x = c x v y = c y w 旋转变换 [ cos θ sin θ 0 − sin θ cos θ 0 0 0 1 ] x = v cos θ − w sin θ y = v sin θ + w cos θ 平移变换 [ 1 0 0 0 1 0 t x t y 1 ] x = v + t x y = w + t y 垂直偏移变换 [ 1 0 0 s v 1 0 0 0 1 ] x = v + s v w y = w 水平偏移变换 [ 1 s h 0 0 1 0 0 0 1 ] x = v y = s h v + w 仿射变换 \\ \begin{array} {ccc} \hline 变换名称 & 仿射矩阵 & 坐标公式\\ \hline 恒等变换 & \begin{bmatrix}1&0&0\\ 0&1&0\\ 0&0&1\end{bmatrix} &\begin{gathered}x=v \\y=w \end{gathered}\\ 尺度变换 & \begin{bmatrix}c_x&0&0\\ 0&c_y&0\\ 0&0&1\end{bmatrix} & \begin{gathered} x=c_xv \\ y=c_yw \end{gathered} \\ 旋转变换 & \begin{bmatrix}\cos\theta&\sin\theta&0\\ -\sin\theta&\cos\theta&0\\ 0&0&1\end{bmatrix} & \begin{gathered} x=v\cos\theta-w\sin\theta \\ y=v\sin\theta+w\cos\theta \end{gathered} \\ 平移变换 & \begin{bmatrix}1&0&0\\ 0&1&0\\ t_x&t_y&1\end{bmatrix} &\begin{gathered}x=v+t_x \\y=w+t_y \end{gathered}\\ 垂直偏移变换 & \begin{bmatrix}1&0&0\\ s_v&1&0\\ 0&0&1\end{bmatrix} &\begin{gathered}x=v+s_vw \\y=w \end{gathered}\\ 水平偏移变换 & \begin{bmatrix}1&s_h&0\\ 0&1&0\\ 0&0&1\end{bmatrix} &\begin{gathered}x=v \\y=s_hv+w \end{gathered}\\ \hline \end{array} 仿射变换变换名称恒等变换尺度变换旋转变换平移变换垂直偏移变换水平偏移变换仿射矩阵 100010001 cx000cy0001 cosθ−sinθ0sinθcosθ0001 10tx01ty001 1sv0010001 100sh10001 坐标公式x=vy=wx=cxvy=cywx=vcosθ−wsinθy=vsinθ+wcosθx=v+txy=w+tyx=v+svwy=wx=vy=shv+w
进行恒等变换、尺度变换、旋转变换、平移变换、垂直变换、水平变换
import math
img = cv2.imread('cv2.png', 0)
n, m = img.shape
n += 100
m += 100
points = []
for i in range(len(img)):
for j in range(len(img[0])):
if img[i][j]:
points.append([i, j])
angle = 3.14/6
mats = [np.array([1, 0, 0, 0, 1, 0, 0, 0, 1]).reshape(3, 3), # 恒等变换
np.array([1.2, 0, 0, 0, 1.2, 0, 0, 0, 1]).reshape(3, 3), # 尺度变换
np.array([math.cos(angle), math.sin(angle), 0, # 旋转变换
-math.sin(angle), math.cos(angle), 0,
0, 0, 1]).reshape(3, 3),
np.array([1, 0, 0, 0, 1, 0, 30, 50, 1]).reshape(3, 3), # 平移变换
np.array([1, 0, 0, 1.1, 1, 0, 0, 0, 1]).reshape(3, 3), # 垂直变换
np.array([1, 1.1, 0, 0, 1, 0, 0, 0, 1]).reshape(3, 3), # 水平变换
]
imgs = []
for mat in mats:
img_t = np.zeros([n, m])
for v, w in points:
x, y, z = np.dot([v, w, 1], mat)
try: # 避免新坐标越界
img_t[int(x)][int(y)] = 254
except:
pass
imgs.append(img_t.astype(np.uint8))
plt_show(imgs[0], imgs[1], imgs[2], imgs[3], imgs[4], imgs[5])
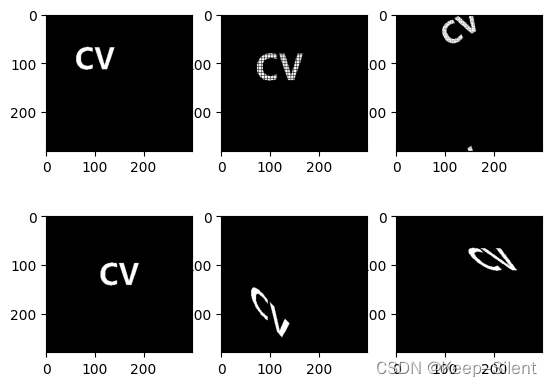
在上图旋转中,旋转时并不是以图片中心为旋转中心,而是以(0,0)为中心,使得中心目标偏移了中心位置。
为使得原目标仍在中心应当(多出1和3步骤):
- 坐标应该扣去中心位置
- 旋转
- 坐标加上中心位置
import math
img = cv2.imread('cv2.png', 0)
n, m = img.shape
n2,m2=n//2,m//2
points = []
for i in range(len(img)):
for j in range(len(img[0])):
if img[i][j]:
points.append([i, j])
angle = 3.14/6
mat = np.array([math.cos(angle), math.sin(angle), 0, # 旋转变换
-math.sin(angle), math.cos(angle), 0,
0, 0, 1]).reshape(3, 3)
img2 = np.zeros([n, m])
for v, w in points:
x, y, z = np.dot([v-n2, w-m2, 1], mat)
try: # 避免新坐标越界
img2[int(x+n2)][int(y+m2)] = 254
except:
pass
img2=img2.astype(np.uint8)
plt_show(img,img2)
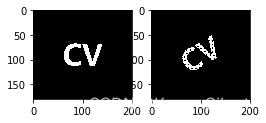
图像配准
img:原图,坐标
(
x
,
y
)
(x,y)
(x,y)
img2:img进行水平垂直变换,坐标
(
v
,
w
)
(v,w)
(v,w)
img3:img2采用双线性模型,进行变化,尝试得到原图。即
x
=
c
1
v
+
c
2
w
+
c
3
v
w
+
c
4
y
=
c
5
v
+
c
6
w
+
c
7
v
w
+
c
8
\begin{gathered} x=c_{1}v+c_{2}w+c_{3}v w+c_{4} \\ y=c_{5}v+c_{6}w+c_{7}v w+c_{8} \end{gathered}
x=c1v+c2w+c3vw+c4y=c5v+c6w+c7vw+c8img4:对比img2和img3的区别。
img = cv2.imread('am.png', 0)
print(img.shape)
n,m=img.shape
det1=0.2
det2=0.05
img2=np.zeros([int(n+m*det1),int(m+n*det2)])
print(img2.shape)
mat=np.array([1, det2, 0, det1, 1, 0, 0, 0, 1]).reshape(3, 3)
for x in range(n):
for y in range(m):
v,w,z=np.dot([x,y,1],mat)
img2[int(v)][int(w)]=img[x][y]
img2=img2.astype(np.uint8)
img3=np.zeros([n,m])
c = [0,
1/(1-det1*det2),-det1/(1-det1*det2),0,0,
-det2/(1-det1*det2),1/(1-det1*det2),0,0
]
for v in range(len(img2)):
for w in range(len(img2[v])):
try:
x,y=c[1]*v+c[2]*w+c[3]*v*w+c[4],c[5]*v+c[6]*w+c[7]*v*w+c[8]
img3[int(x)][int(y)]=img2[v][w]
except:
pass
img3=img3.astype(np.uint8)
img4=img-img3
# x,y=c[1]*v+c[2]*w+c[3]*v*w+c[4],c[5]*v+c[6]*w+c[7]*v*w+c[8]
# print(print(str([v,w])+'->'+str([int(x),int(y)])))
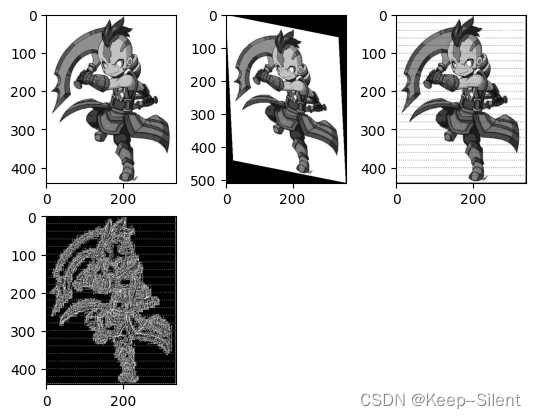
plt_show(img,img2,img3,img4)
(440, 340)
(508, 362)
2.6.6向量与矩阵操作
一个像素有三个分量(RGB),组成列向量形式
z
=
[
z
1
,
z
2
,
z
3
]
T
z=[z_1,z_2,z_3]^T
z=[z1,z2,z3]T。
z与a的欧式距离
D
(
z
,
a
)
=
[
(
z
−
a
)
T
(
z
−
a
)
]
1
2
=
[
(
z
1
−
a
1
)
2
+
(
z
2
−
a
2
)
2
+
⋯
+
(
z
n
−
a
n
)
2
]
1
2
D(z,a)=\left[(z-a)^{\text{T}}(\text{z}-a)\right]^{\frac{1}{2}}=\left[(z_1-a_1)^2+(z_2-a_2)^2+\cdots+(z_n-a_n)^2\right]^{\frac{1}{2}}
D(z,a)=[(z−a)T(z−a)]21=[(z1−a1)2+(z2−a2)2+⋯+(zn−an)2]21
2.6.7图像变换
表示为
T
(
u
,
v
)
T(u,v)
T(u,v)的二维线性变换的通用形式为
T
(
u
,
v
)
=
∑
x
=
0
M
−
1
∑
y
=
0
N
−
1
f
(
x
,
y
)
r
(
x
,
y
,
u
,
v
)
T(u,v)=\sum_{x=0}^{M-1}\sum_{y=0}^{N-1}f(x,y)r(x,y,u,v)
T(u,v)=x=0∑M−1y=0∑N−1f(x,y)r(x,y,u,v)
其中
f
(
x
,
y
)
f(x,y)
f(x,y)是输入图像,
r
(
x
,
y
,
u
,
v
)
r(x,y,u,v)
r(x,y,u,v)是正变换核,
T
(
u
,
v
)
T(u,v)
T(u,v)称为
f
(
x
,
y
)
f(x,y)
f(x,y)的正变换。给定
T
(
u
,
v
)
T(u,v)
T(u,v),可以反变换还原
f
(
x
,
y
)
f(x,y)
f(x,y):
f
(
x
,
y
)
=
∑
u
=
0
M
−
1
∑
v
=
0
N
−
1
T
(
u
,
v
)
s
(
x
,
y
,
u
,
v
)
f(x,y)=\sum_{u=0}^{M-1}\sum_{v=0}^{N-1}T(u,v)s(x,y,u,v)
f(x,y)=u=0∑M−1v=0∑N−1T(u,v)s(x,y,u,v)
s ( x , y , u , v ) s(x,y,u,v) s(x,y,u,v)称之为反变换核。
线性变换域中操作的一般方法: f ( x , y ) → 变换 ⟶ T ( u , v ) 运算 R ⟶ R [ T ( u , v ) ] 反变换 → g ( x , y ) f(x,y)\rightarrow变换 \stackrel{T(u,v)} \longrightarrow运算R \stackrel{R[T(u,v)]} \longrightarrow 反变换 \rightarrow g(x,y) f(x,y)→变换⟶T(u,v)运算R⟶R[T(u,v)]反变换→g(x,y)
例2.11变换域图像处理
图2.40 显示了上诉式子的一个例子。在这种情况下,所用的变换是傅里叶变换,在本节稍后我们将简单提一下它,第4章将对其进行详细介绍。图2.40(a)是一幅被正弦干扰污染了的图像,图2.40(b)是该图像傅里叶变换的幅度,它是图2.39中第一阶段的输出。空间域中的正弦干扰在变换域以较亮的脉冲方式出现。在这种情况下,脉冲是图2.40(b)中可见的圆形模式。图2.40©显示了一个模板图像(称为滤波器),白和黑分别代表1和0。对于该例子,图2.39第二个方框内的操作是变换的结果与模板相乘,以可靠地消除干扰脉冲。图2.40(d)显示了最终结果,该结果是通过计算修改后的变换的反变换得到的。事实上,您恰好可以看到基准标志(淡淡的十字),它用于图像对准。

如果 r ( x , y , u , v ) = r 1 ( x , u ) r 2 ( y , v ) r(x,y,u,v)=r_1(x,u)r_2(y,v) r(x,y,u,v)=r1(x,u)r2(y,v) 则正向变换核可分,如果 r 1 ( x , y ) = r 2 ( x , y ) r_1(x,y)=r_2(x,y) r1(x,y)=r2(x,y) ,则称变换核是对称的,从而有 r ( x , y , u , v ) = r 1 ( x , u ) r 1 ( y , v ) r(x,y,u,v)=r_1(x,u)r_1(y,v) r(x,y,u,v)=r1(x,u)r1(y,v)
例2.11中的二维傅里叶变换的正反变换核( j = − 1 j=\sqrt{-1} j=−1): r ( x , y , u , v ) = e − j 2 π ( u x M + v y N ) r(x,y,u,v)=e^{-j2\pi (\frac{ux}{M}+\frac{vy}{N})} r(x,y,u,v)=e−j2π(Mux+Nvy) s ( x , y , u , v ) = e j 2 π ( u x M + v y N ) M N s(x,y,u,v)=\cfrac{e^{j2\pi (\frac{ux}{M}+\frac{vy}{N})}}{MN} s(x,y,u,v)=MNej2π(Mux+Nvy)
可得出离散傅里叶变换对 T ( u , v ) = ∑ x = 0 M − 1 ∑ y = 0 N − 1 f ( x , y ) r ( x , y , u , v ) = ∑ x = 0 M − 1 ∑ y = 0 N − 1 f ( x , y ) e − j 2 π ( u x M + v y N ) T(u,v)=\sum_{x=0}^{M-1}\sum_{y=0}^{N-1}f(x,y)r(x,y,u,v)=\sum_{x=0}^{M-1}\sum_{y=0}^{N-1}f(x,y)e^{-j2\pi (\frac{ux}{M}+\frac{vy}{N})} T(u,v)=x=0∑M−1y=0∑N−1f(x,y)r(x,y,u,v)=x=0∑M−1y=0∑N−1f(x,y)e−j2π(Mux+Nvy) f ( x , y ) = ∑ u = 0 M − 1 ∑ v = 0 N − 1 T ( u , v ) s ( x , y , u , v ) = ∑ u = 0 M − 1 ∑ v = 0 N − 1 T ( u , v ) e j 2 π ( u x M + v y N ) M N f(x,y)=\sum_{u=0}^{M-1}\sum_{v=0}^{N-1}T(u,v)s(x,y,u,v)=\sum_{u=0}^{M-1}\sum_{v=0}^{N-1}T(u,v)\cfrac{e^{j2\pi (\frac{ux}{M}+\frac{vy}{N})}}{MN} f(x,y)=u=0∑M−1v=0∑N−1T(u,v)s(x,y,u,v)=u=0∑M−1v=0∑N−1T(u,v)MNej2π(Mux+Nvy)
2.6.8概率方法
令 z i ( i = 0 , 1 , … , L − 1 ) z_i(i=0,1,\dots, L-1) zi(i=0,1,…,L−1) 表示一幅M*N大小数字图像中所有可能的灰度值,则在给定图像中灰度级 z k z_k zk出现的概率 p ( z k ) p(z_k) p(zk)为 p ( z k ) = n k M N p(z_k)=\cfrac{n_k}{MN} p(zk)=MNnk其中, n k n_k nk是灰度 z k z_k zk在图像中出现的次数,MN是图像总数。显然: ∑ k = 0 L − 1 p ( z k ) = 1 \sum_{k=0}^{L-1}p(z_k)=1 k=0∑L−1p(zk)=1 。一旦知道 p ( z k ) p(z_k) p(zk) ,就可以得出许多图像特性。例如,平均灰度为: m = ∑ k = 0 L − 1 z k p ( z k ) m=\sum_{k=0}^{L-1}z_kp(z_k) m=k=0∑L−1zkp(zk)方差为 σ 2 = ∑ k = 0 L − 1 ( z k − m ) 2 p ( z k ) \sigma^2=\sum_{k=0}^{L-1}(z_k-m)^2p(z_k) σ2=k=0∑L−1(zk−m)2p(zk)方差是 z z z值关于均值的展开度的度量,因此它是图像对比度的有用度量。通常,随机变量 z z z关于均值的第 n n n阶矩定义为 μ n ( z ) = ∑ k = 0 L − 1 ( z k − m ) n p ( z k ) \mu_n(z)=\sum_{k=0}^{L-1}(z_k-m)^n p(z_k) μn(z)=k=0∑L−1(zk−m)np(zk)可知 μ 0 ( z ) = 1 , μ 1 ( z ) = 0 且 μ 2 ( z ) = σ 2 \mu_0(z)=1,\mu_1(z)=0 且\mu_2(z)=\sigma^2 μ0(z)=1,μ1(z)=0且μ2(z)=σ2,均值和方差对图像的视觉特性有明显的直接关系,高阶矩更敏感。