leecode530 二叉搜索树的最小绝对差

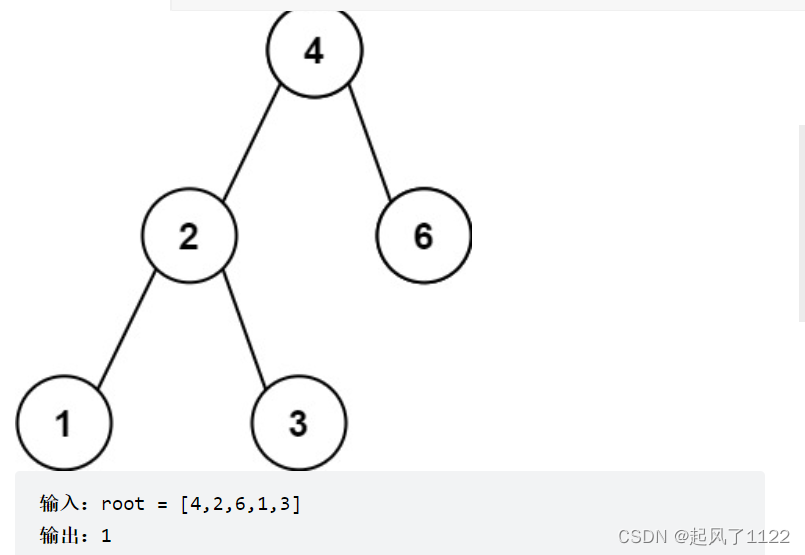
🔎首先要知道二叉搜索树是有序的，补充一下二叉搜索树的相关概念。

🟠 对于 BST 的每一个节点 node，左子树节点的值都比 node 的值要小，右子树节点的值都比 node 的值大。

🟠 对于 BST 的每一个节点 node，它的左侧子树和右侧子树都是 二叉搜索树。

🟠从做算法题的角度来看 BST，除了它的定义，还有一个重要的性质：BST 的中序遍历结果是有序的（升序）。

🌻在二叉搜索树中，可能会经常看到类似下面这样的代码逻辑：

void BST(TreeNode root, int target) {
    if (root.val == target)
        // 找到目标，做点什么
    if (root.val < target) 
        BST(root.right, target);
    if (root.val > target)
        BST(root.left, target);
}

如果遇到在二叉搜索树上求差值、最值等，就把他想象成在一个有序数组上求最值、差值。
二叉搜索树如果采用中序遍历，就是一个有序数组。
在一个有序数组上求最值岂不是很简单。

🔎递归法

🔎思路：

🌼1.首先定义一个pre节点为空，用来保存上一个节点

🌼2.定义一个接收结果的res变量，初始值假设为最大值。

🌼3.当这棵树为空的时候，返回0；不为空的时候，调用函数trversal，对根节点的左子树和右子树进行判断计算。

🌼4.如果当前搜索树的根节点的不为空，调用当前根节点的左节点，当pre指针不为空的时候，计算当前节点值和上一个节点的最小差值保存到result变量中。（只有pre不为空的情况下才能计算差值），令pre等于当前节点，以便于后续进行计算。

🌼5.遍历右子树，同上步骤。

class Solution {
    TreeNode pre;// 记录上一个遍历的结点
    int result = Integer.MAX_VALUE;
    public int getMinimumDifference(TreeNode root) {
       if(root==null)return 0;
       traversal(root);
       return result;
    }
    public void traversal(TreeNode root){
        if(root==null)return;
        //左
        traversal(root.left);
        //中
        if(pre!=null){
            result = Math.min(result,root.val-pre.val);
        }
        pre = root;
        //右
        traversal(root.right);
    }
}