1. 引言

前序博客有：

• Polygon zkEVM的pil-stark Fibonacci状态机初体验
• Polygon zkEVM的pil-stark Fibonacci状态机代码解析
• rank-1 constraint system R1CS

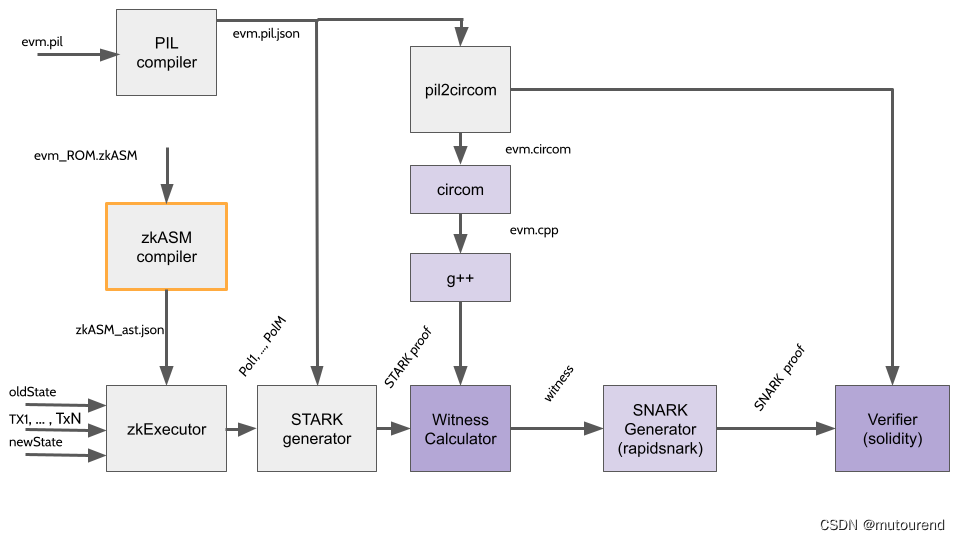
由上图可知，zkEVM会借助SNARK来“验证（（验证STARK证明）的SNARK证明）”：

• 1）将 STARK proof的约束系统evm.pil 经 pil2circom 转换为 evm.verifier.cricom格式。详细见 Polygon zkEVM的pil-stark Fibonacci状态机初体验 第2节第8步“fibonacci generate circom”。
• 2）再借助 circom工具 将 STARK约束系统 转换为 R1CS约束系统表示evm.verifier.r1cs。详细见 Polygon zkEVM的pil-stark Fibonacci状态机初体验 第2节第9步“”
• 3）再经 Compressor12_setup 将 R1CS约束系统表示evm.verifier.r1cs 转换为 Plonk约束表示，同时会生成与 Plonk约束表示 对应的 STARK约束evm.c12.pil，以及 constant多项式的execution trace evm.c12.const 和 Plonk辅助信息 evm.c12.exec。详细见 Polygon zkEVM的pil-stark Fibonacci状态机初体验 第2节第10步“fibonacci C12 setup”。Plonk辅助信息 evm.c12.exec 会用于后续生成 commit多项式execution trace evm.c12.commit。

2. 约束表达

约束表达：

• 1）STARK：采用execution trace来表示约束，以表格形式来表示内部程序状态的变化。如：

  序号	$x$	$\mathbf{A}$（$l_2(x)$多项式）	$\mathbf{B}$（$l_1(x)$多项式）	$\mathbf{i}\mathbf{s}\mathbf{I}\mathbf{n}\mathbf{i}\mathbf{t}\mathbf{i}\mathbf{a}\mathbf{l}$（$L_1(x)$多项式）	$\mathbf{i}\mathbf{s}\mathbf{L}\mathbf{a}\mathbf{s}\mathbf{t}$（$LLAST(x)$多项式）
  0	${\omega }^0$	1	2	1	0
  1	${\omega }^1$	2	5	0	0
  2	${\omega }^2$	5	29	0	0
  $⋮$	$⋮$	$⋮$	$⋮$	$⋮$	$⋮$
  1023	${\omega }^{1023}$	…	74469561660084004	0	1

• 2）Groth16等SNARK方案：采用R1CS来表示约束，形如$<\vec{s},\vec{a}>\ast <\vec{s},\vec{b}>-<\vec{s},\vec{c}>=0$，其中$<\vec{s},\vec{a}>={\sum }_{i=1}^n{s}_i{a}_i$为dot product，$\vec{a},\vec{b},\vec{c}$为每步计算的系数，$\vec{s}$为相应的输入。
• 3）Halo2等SNARK方案：采用Plonk来表示约束，形如$Q_m\ast x_r\ast x_l+Q_l\ast x_l+Q_r\ast x_r+Q_o\ast x_o+Q_k=0$，其中$Q_m,Q_l,Q_r,Q_o,Q_k$均为selector，$x_l,x_r,x_o$为相应的输入。

以PIL-STARK 中的Fibonacci为例，在验证其STARK proof的Plonk表达中，除以上$Q_m,Q_l,Q_r,Q_o,Q_k$ selector之外，还额外引入了定制门 selector $Q_{MDS},Q_{CMUL}$。

附录：Polygon Hermez 2.0 zkEVM系列博客

• ZK-Rollups工作原理
• Polygon zkEVM——Hermez 2.0简介
• Polygon zkEVM网络节点
• Polygon zkEVM 基本概念
• Polygon zkEVM Prover
• Polygon zkEVM工具——PIL和CIRCOM
• Polygon zkEVM节点代码解析
• Polygon zkEVM的pil-stark Fibonacci状态机初体验
• Polygon zkEVM的pil-stark Fibonacci状态机代码解析
• Polygon zkEVM PIL编译器——pilcom 代码解析
• Polygon zkEVM Arithmetic状态机
• Polygon zkEVM中的常量多项式
• Polygon zkEVM Binary状态机
• Polygon zkEVM Memory状态机
• Polygon zkEVM Memory Align状态机
• Polygon zkEVM zkASM编译器——zkasmcom
• Polygon zkEVM哈希状态机——Keccak-256和Poseidon
• Polygon zkEVM zkASM语法
• Polygon zkEVM可验证计算简单状态机示例
• Polygon zkEVM zkASM 与 以太坊虚拟机opcode 对应集合
• Polygon zkEVM zkROM代码解析（1）
• Polygon zkEVM zkASM中的函数集合
• Polygon zkEVM zkROM代码解析（2）
• Polygon zkEVM zkROM代码解析（3）
• Polygon zkEVM公式梳理
• Polygon zkEVM中的Merkle tree
• Polygon zkEVM中Goldilocks域元素circom约束
• Polygon zkEVM Merkle tree的circom约束
• Polygon zkEVM FFT和多项式evaluate计算的circom约束