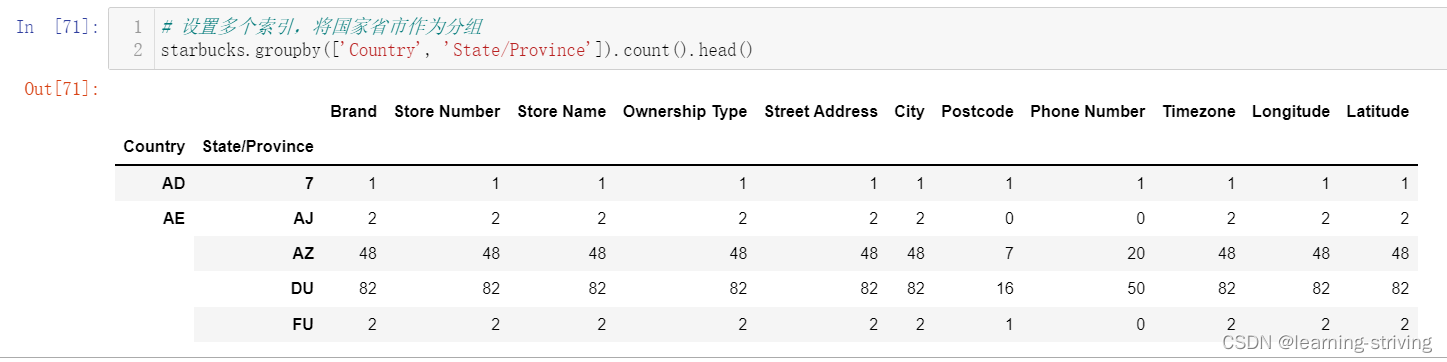
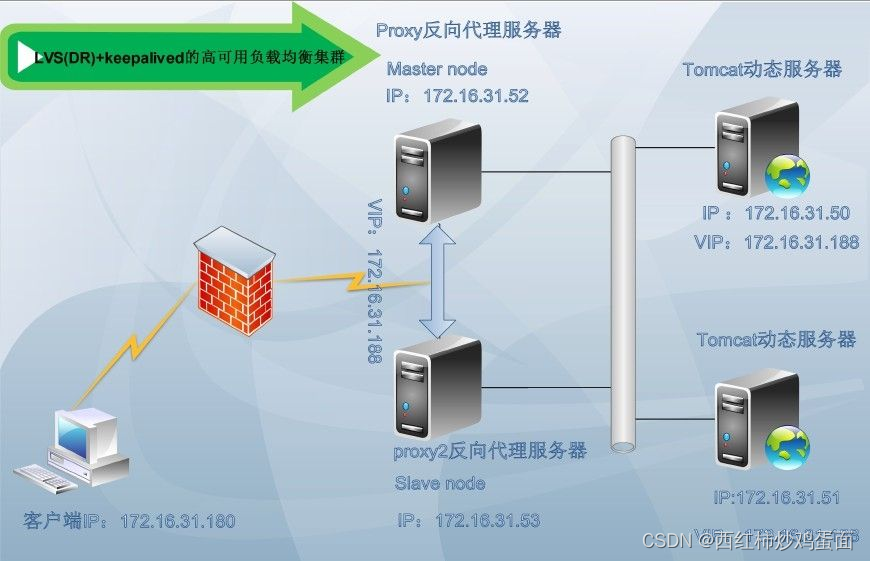
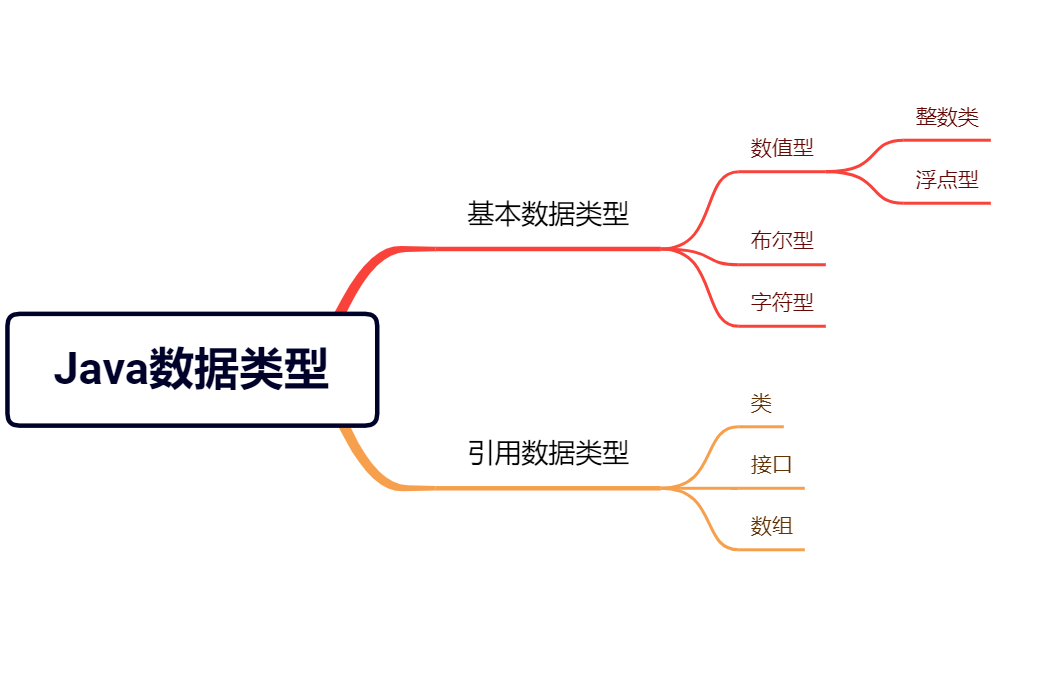
为了考察总体X 的分布,我们将在2.4 节给出经验分布函数,并在总体X为连续型情形下绘制了频率直方图从中可大致看出总体的分布情况或分布形式,但总体分布中包含的参数往往不知.如何根据抽样对未知参数进行估计,就是本章讨论的问题之一. 有时即使不知道总体的分布形式,我们也希望能通过参数估计找到反映总体特征的未知参数.本章前三节就在这两种情形下讨论参数的估计问题. 为方便,本章前三节及以后各章仍采用第1章给出的有关记号.
样本源于总体,带有总体的特性.因此, 为了找到反映总体分布或反映总体特征的某个未知参数,我们自然想到通过样本
,构造某个统计量
![]()
作为总体参数的估计. 相对于后面的区间估计而言,我们称这样的估计为参数的
点估计, 而称由式(2. 1) 给出的估计量为的点估计量.若
为样本
的一个观测值,则称
为
的点估计值.
下面介绍求参数点估计的两种方法.
2. 1. 1 矩估计法
设是来自总体X的样本,则由辛钦大数定律知,当总体的K阶原点矩
存在时,样本的k阶原点矩依概率收敛于总体的k阶原点矩,即
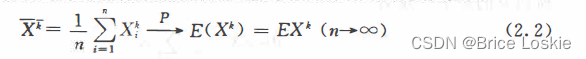
因此,我们自然用样本的K阶原点矩作为总体K阶原点矩的估计.
设北是反映总体分布或总体特征的r个未知参数,则总体的前r阶原点矩(设都存在)就应该是
的函数令它们为相应的总体原点矩,即得矩估计方程组
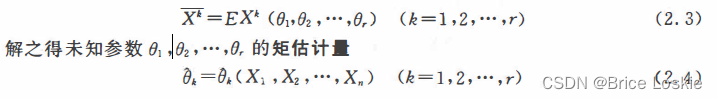
这种求参数的估计法称为矩估计法.

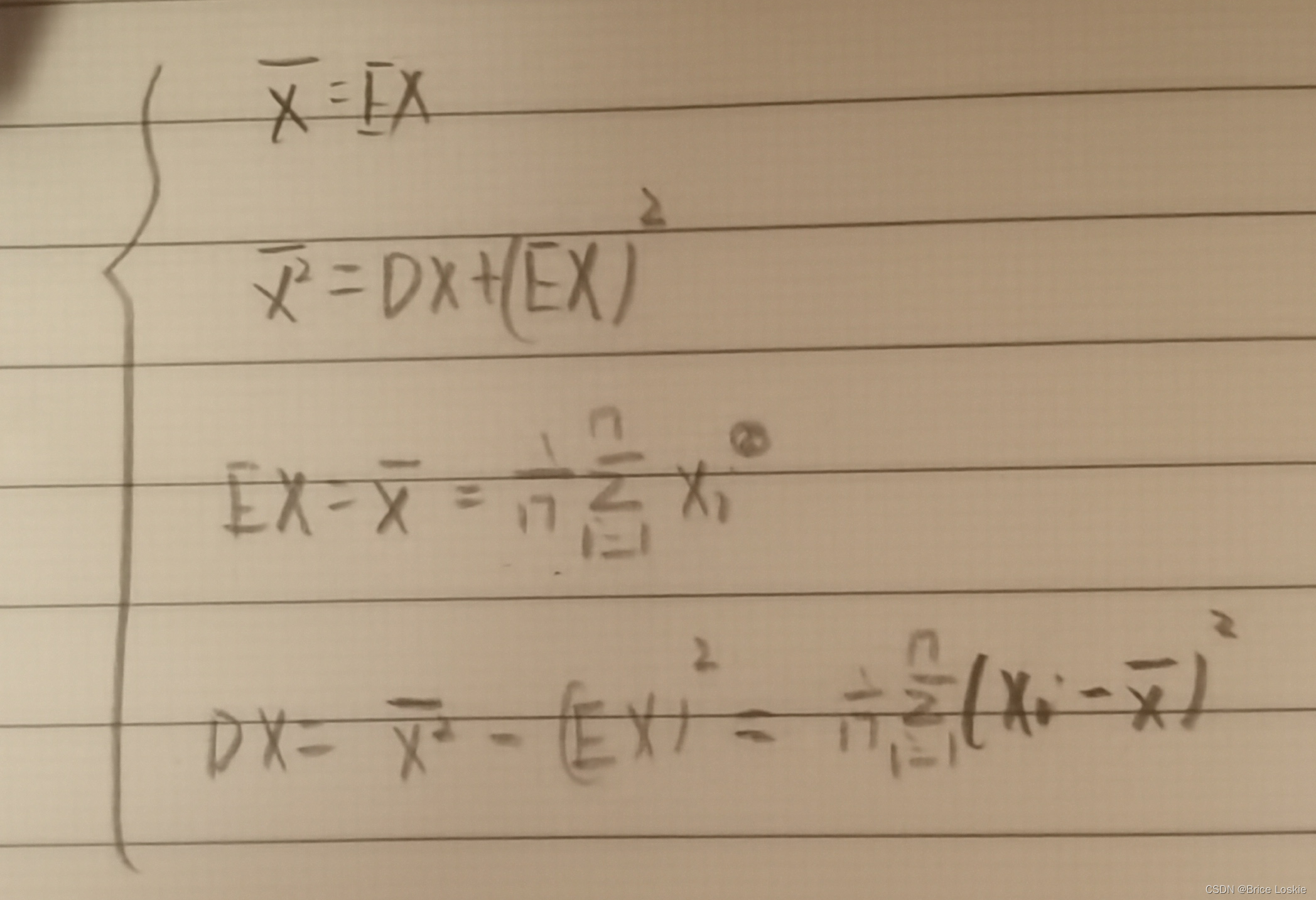



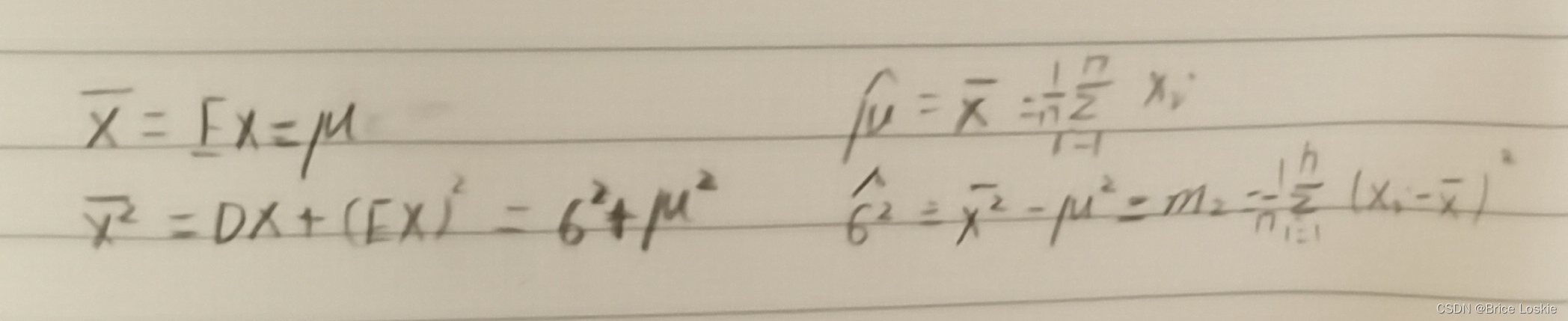
从解题过程可知, 这个结论不仅对正态总体成立,而且有下面的结论.
结论无论总体X服从什么分布,只要总体的均值与方差存在,总体均值EX的矩估计都是样本均值;总体方差DX的矩估计都是样本的二阶中心矩
2. 1. 2 极大似然估计法
设总体X是离散型随机变量,其分布律为
![]()
其中是未知参数.设
为来自总体X 的样本,
是一个样本观测值. 那么作为n维随机变量,
在点
取值的概率(即n维随机变量
的联合分布律)为
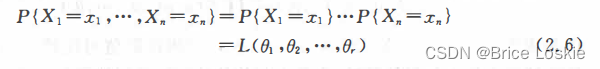
其中
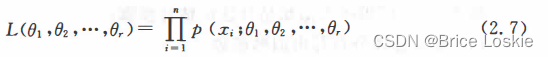
是的函数,称为样本的似然函数.极大似然估计法(也称最大似然估计
法)的直观想法就是:既然作为样本的一次观测值已经出现,根据实
际推断原理的选取就应有利于样本的观测值
出现,即
我们应当选取这样的使样本
取得样本观测值
的概率(2. 6)或似然函数(2. 7)达到最大.即
![]()
这样得到的估计与样本观测值有关,记作
![]()
称为参数的极大似然估计值.


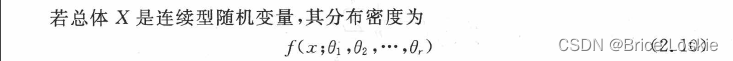


![]()
![]()

![]()

![]()
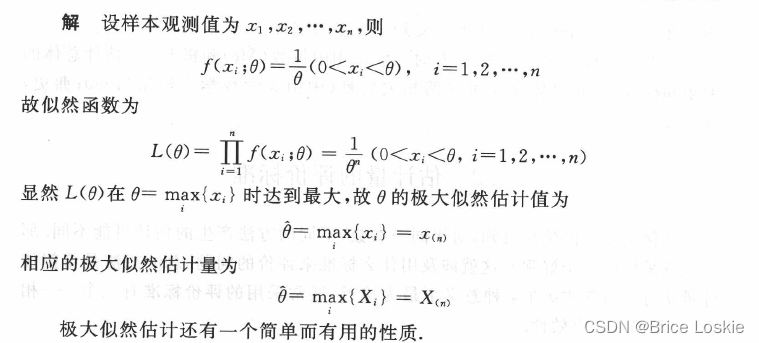
定理2. 1. 1 设是参数
的一个极大似然估计,函数
具有单值反单调性,则
![]()
就是的极大似然估计.