⭐️前言⭐️
本篇文章主要分享几道贪心算法的题目,贪心算法是一种基于自然智慧的算法,这类题目并没有统一的解法,但通常都是每一步做出一个局部最优的选择,最终的结果就是全局最优。
🍉欢迎点赞 👍 收藏 ⭐留言评论 📝私信必回哟😁
🍉博主将持续更新学习记录收获,友友们有任何问题可以在评论区留言
🍉博客中涉及源码及博主日常练习代码均已上传GitHub

📍内容导读📍
- 🍅字典序最小
- 🍅会议安排
- 🍅分金条
- 🍅最大钱数
- 🍅安灯
🍅字典序最小
题目:
给定一个由字符串组成的数组strs,必须把所有的字符串拼接起来,返回所有可能的拼接结果中字典序最小的结果。
代码实现:
public class LowestString {
public static class MyComparator implements Comparator<String> {
@Override
public int compare(String o1, String o2) {
return (o1+o2).compareTo(o2+o1);
}
}
public static String lowestString(String[] strs) {
if(strs==null||strs.length==0) {
return "";
}
Arrays.sort(strs,new MyComparator());
StringBuilder res=new StringBuilder();
for (int i = 0; i < strs.length; i++) {
res.append(strs[i]);
}
return res.toString();
}
}
🍅会议安排
题目:
一些项目要占用一个会议室宣讲,会议室不能同时容纳两个项目的宣讲,给你每一个项目开始的时间和结束的时间
你来安排宣讲的日程,要求会议室进行的宣讲的场次最多,返回最多的宣讲场次
题解思路:
贪心策略为按会议的结束时间排序,没有冲突的全部囊括即为最终结果。
代码实现:
public class BestArrange {
public static class Program {
public int start;
public int end;
public Program(int start, int end) {
this.start = start;
this.end = end;
}
}
public static int bestArrange(Program[] programs) {
Arrays.sort(programs, new Comparator<Program>() {
@Override
public int compare(Program o1, Program o2) {
return o1.end-o2.end;
}
});
int timeLine=0;
int result=0;
// 依次遍历每一个会议,结束时间早的会议优先遍历
for (int i = 0; i < programs.length; i++) {
if(timeLine<=programs[i].start) {
result++;
timeLine=programs[i].end;
}
}
return result;
}
}
🍅分金条
题目:
一块金条切成两半,是需要花费和长度数值一样的铜板
比如长度为20的金条,不管怎么切都要花费20个铜板,一群人想整分整块金条,怎么分最省铜板?
例如,给定数组{10,20,30},代表一共三个人,整块金条长度为60,金条要分成10,20,30三个部分。
如果先把长度60的金条分成10和50,花费60;再把长度50的金条分成20和30,花费50;一共花费110铜板
但如果先把长度60的金条分成30和30,花费60;再把长度30金条分成10和20,花费30;一共花费90铜板
输入一个数组,返回分割的最小代价。
题解思路:
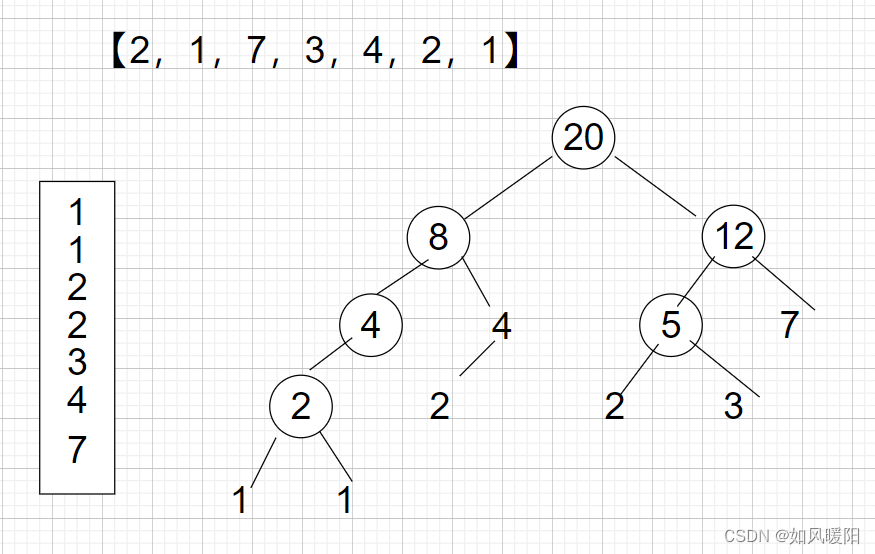
哈夫曼编码思想,借助优先级队列(小根堆),每次弹出两个数,合成一个数后再放入队列,直到最终队列中的数变为数组总和。
耗费的代价即为圈中数字和。
代码实现:
public class LessMoney {
public static int lessMoney(int[] arr) {
PriorityQueue<Integer> queue=new PriorityQueue<>();
for (int i = 0; i < arr.length; i++) {
queue.add(arr[i]);
}
int sum=0;
int cur=0;
while (queue.size()>1) {
cur=queue.poll()+queue.poll();
sum+=cur;
queue.offer(cur);
}
return sum;
}
}
🍅最大钱数
题目:
输入正数数组costs、正数数组profits、正数K和正数M
costs[i]表示i号项目的花费
profits[i]表示i号项目在扣除花费之后还能挣到的钱(利润)
K表示你只能串行的最多做k个项目
M表示你初始的资金
说明:每做完一个项目,马上获得的收益,可以支持你去做下一个项目,不能并行的做项目。
输出:最后获得的最大钱数
题解思路:
需要两个数据结构,一个是小根堆(以花费做比较),另一个是大根堆(以利润做比较)
根据M来解锁小根堆中可以做的项目,让其进入大根堆,然后大根堆弹出堆顶元素,M变动,数量++,重新之前的操作,直到数量到达K。
(思路来源于打怪升级的过程,在能力范围内,找能提升等级最大的怪打,打完以后再用新的能力来权衡能提升等级最大的怪)
代码实现:
public class IPO {
public static class Program {
public int cost;
public int profit;
public Program(int profit, int cost) {
this.cost = cost;
this.profit = profit;
}
}
public static int findMaximizedCapital(int K,int W,int[] costs,int[] profits) {
PriorityQueue<Program> minCostQueue=new PriorityQueue<>(new Comparator<Program>() {
@Override
public int compare(Program o1, Program o2) {
return o1.cost- o2.cost;
}
});
PriorityQueue<Program> maxProfitQueue=new PriorityQueue<>(new Comparator<Program>() {
@Override
public int compare(Program o1, Program o2) {
return o2.profit- o2.profit;
}
});
for (int i = 0; i < costs.length; i++) {
minCostQueue.add(new Program(costs[i],profits[i]));
}
for (int i = 0; i < K; i++) {
while (!minCostQueue.isEmpty()&&minCostQueue.peek().cost<=W) {
maxProfitQueue.add(minCostQueue.poll());
}
if(maxProfitQueue.isEmpty()) {
return W;
}
W+=maxProfitQueue.poll().profit;
}
return W;
}
}
🍅安灯
题目:
给定一个字符串str,只由’X’和’.'两种字符构成
‘X’表示墙,不能放灯,也不需要点亮;’.'表示居民点,可以放灯,需要点亮
如果灯放在i位置,可以让i-1,i和i+1三个位置被点亮
返回如果点亮str中所有需要点亮的位置,至少需要几盏灯
题解思路:
直接把字符串以"X"分割开来,因为只需要考虑居民点部分的照亮,一盏灯最多照亮三个点,所以就让每块分割开的字符串长度除以三,并向上取整,就是最终结果。
代码实现:
public static int minLight(String road) {
String[] ss=road.split("X");
int light=0;
for(String s:ss) {
light+=(s.length()+2)/3;
}
return light;
}
⭐️最后的话⭐️
总结不易,希望uu们不要吝啬你们的👍哟(^U^)ノ~YO!!如有问题,欢迎评论区批评指正😁