给你二叉树的根节点 root 和一个整数 limit ，请你同时删除树中所有 不足节点 ，并返回最终二叉树的根节点。

假如通过节点 node 的每种可能的 “根-叶” 路径上值的总和全都小于给定的 limit，则该节点被称之为 不足节点 ，需要被删除。

叶子节点，就是没有子节点的节点。

示例 1：

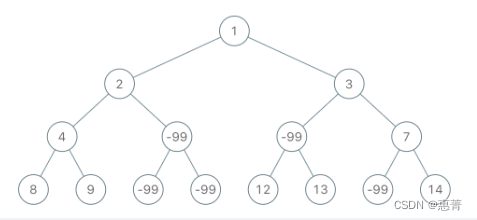
输入：root = [1,2,3,4,-99,-99,7,8,9,-99,-99,12,13,-99,14], limit = 1
输出：[1,2,3,4,null,null,7,8,9,null,14]
示例 2：

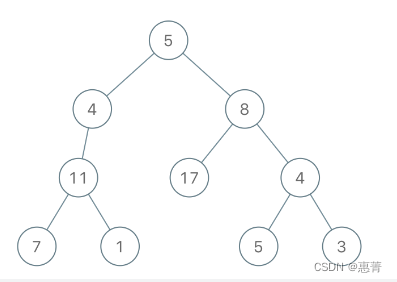
输入：root = [5,4,8,11,null,17,4,7,1,null,null,5,3], limit = 22
输出：[5,4,8,11,null,17,4,7,null,null,null,5]
示例 3：

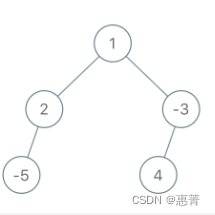
输入：root = [1,2,-3,-5,null,4,null], limit = -1
输出：[1,null,-3,4]

提示：

树中节点数目在范围 [1, 5000] 内
-105 <= Node.val <= 105
-109 <= limit <= 109

    public TreeNode sufficientSubset(TreeNode root, int limit) {
        dfs(root,limit,0);
        return root;
    }
    public TreeNode dfs(TreeNode root, int limit,int sum){
        if (root==null){
            return null;
        }
        sum+=root.val;
        if (root.left==null&&root.right==null){
            return sum<limit?null:root;
        }
        root.left=dfs(root.left,limit,sum);
        root.right=dfs(root.right,limit,sum);
        return root.left==null&&root.right==null?null:root;
    }

func sufficientSubset(root *TreeNode, limit int) *TreeNode  {
	return dfs(root,limit,0)
}
func dfs(root *TreeNode, limit, sum int) *TreeNode {
	if root == nil {
		return nil
	}
	sum += root.Val
	if root.Left == nil && root.Right == nil {
		if sum < limit {
			return nil
		}
		return root
	}
	root.Left = dfs(root.Left, limit, sum)
	root.Right = dfs(root.Right, limit, sum)
	if root.Left == nil && root.Right == nil {
		return nil
	}
	return root
}