目录

最大公约数

手写GCD

最小公倍数

推导LCM函数表达式

GCD基本性质

性质的证明

取模运算基本性质

证明

---

最大公约数

gcd是最大公约数的意思。Python的math库里有gcd函数。

在Python命令行运行gcd，可发现其可传入0、不会返回负数、可对多个数进行判断的性质。

from math import *
gcd(0,44)
44
gcd(0,0)
0
gcd(-6,-15)
3
gcd(-17,289)
17
gcd(17,-289)
17
gcd(48,96,120,688)
8

手写GCD

辗转相除法

容易证明，

于是可写如下代码：

def gcd(a,b):
    if b==0:return a
    else: return gcd(b,a%b)

由于在Python中，a%b当b为负数的时候结果为负数，所以此手写算法有可能返回负数。

最小公倍数

lcm是最小公倍数的意思。在Python里有lcm函数，但是蓝桥杯用的环境是Python3.8.6的，所以只能借助gcd函数写lcm函数了。代码如下：

from math import *
def lcm(a,b):
    return a//gcd(a,b)*b

借用表达式。

推导LCM函数表达式

由算数基本定理：任何一个大于1的正整数n，都可以唯一分解成有限个素数的乘积。

则有

是非负整数，是互不相同的素数，且随增大，数值不减。 

设，

则有

所以

则有

GCD基本性质

(1)

(2)

(3)定义多个整数的最大公约数: 

(4)若，则，即与互素。

(5)

性质的证明

取模运算基本性质

请看此篇文章的前五条性质。

最大公约数 —— Greatest Common Divisor(GCD) - 知乎 (zhihu.com)

证明

（1）

（2）

（3）使用算数基本定理证明，不再赘述。

（4）

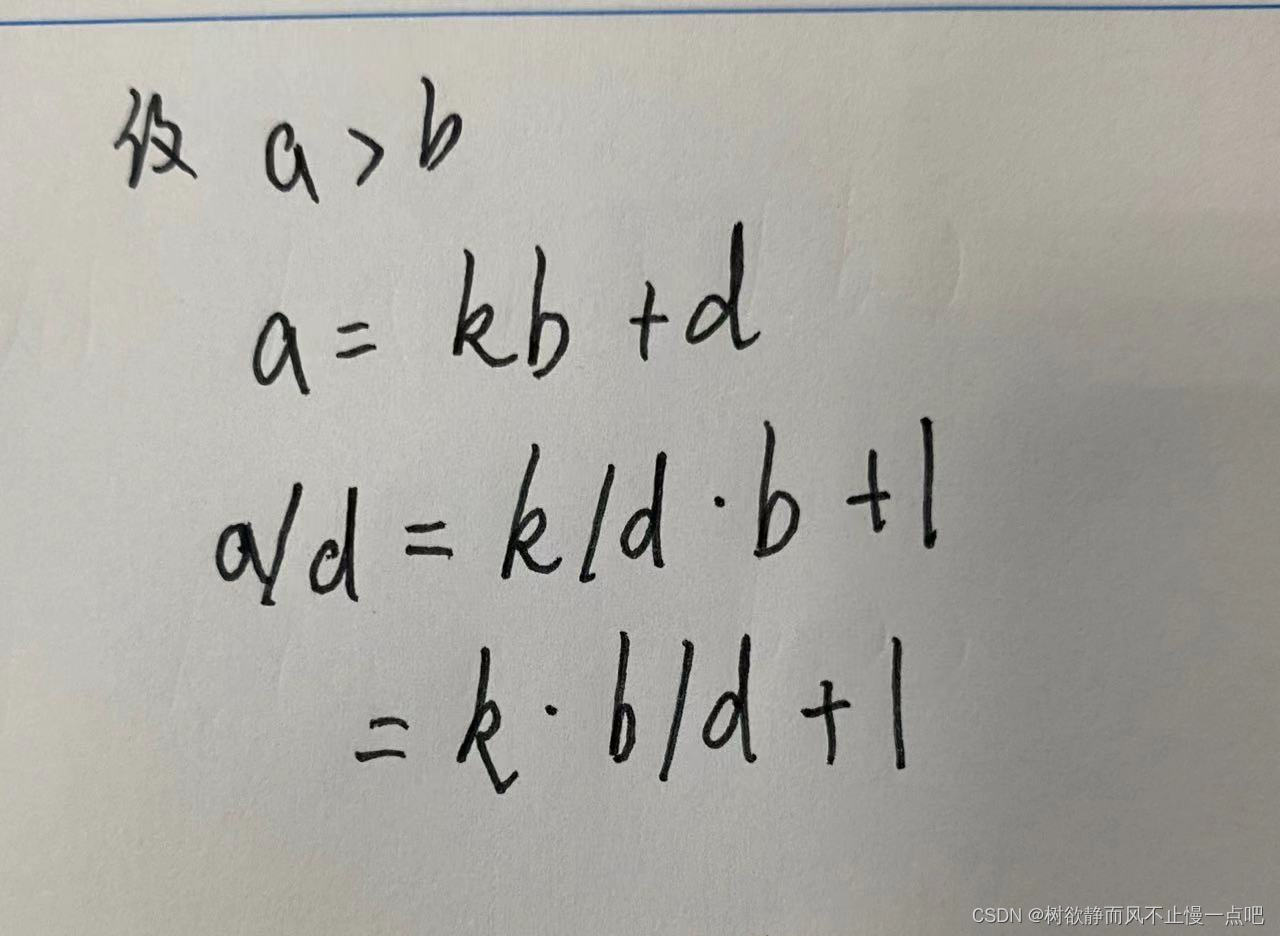
（5）和第一条等价。