2023中兴软件类笔试

1.下列Python代码：将近似输出什么？

import numpy as np
print np.sqrt(6*np.sum(1/np.arange(1,1000000, dtype=np.float)**2))

在这里插入图片描述

这段代码是用来计算圆周率的巴塞尔问题（Basel problem）的近似值，输出结果将近似为3.14159169866。

2.计算机网络中，子网划分是通过借用IP地址的若干位主机位来充当子网地址从而将原网络划分为若干子网而实现的，现假设北京市某单位分配到一个B类IP地址，其网络地址为129.250.0.0，该单位有4000台机器，平均分布在16个不同的地点，试给每一地点分配一个子网号码，要求能分配的子网数最多的情况下，每个子网里面的主机数也能容纳一个地点的所有主机，则子网掩码选择为多少，这种情况下可以划分多少个子网？（）

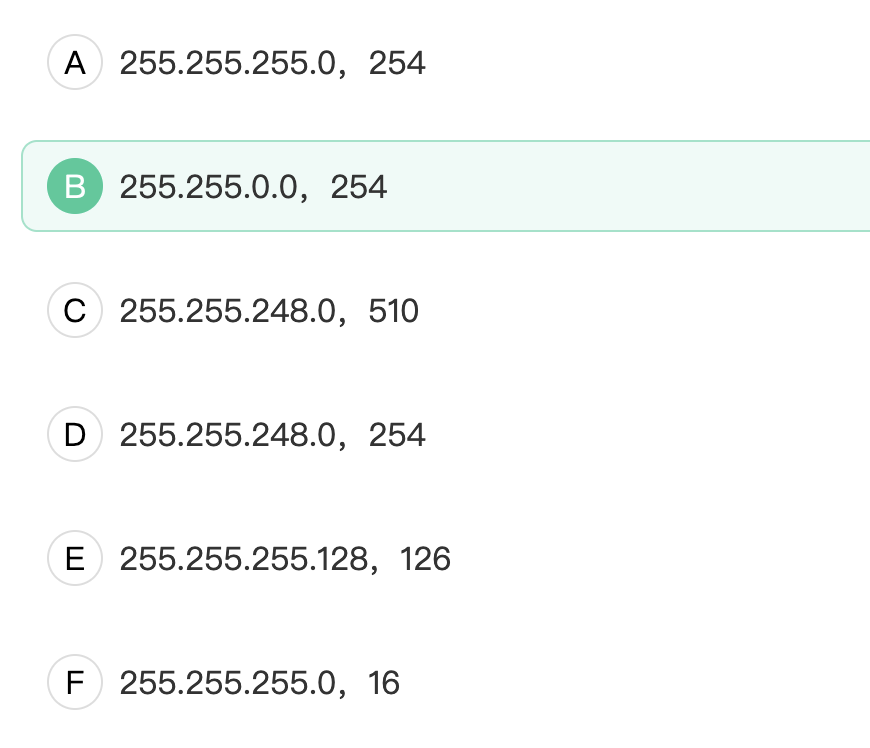
在这里插入图片描述
根据题意，该单位使用B类IP地址，网络地址为129.250.0.0，因此默认子网掩码为255.255.0.0。我们需要从主机位中借用若干位来充当子网地址，以划分出更多的子网。

首先，需要确定每个地点需要的IP地址数量。由于每个地点都有4000台机器，且每个子网里面的主机数也能容纳一个地点的所有主机，因此每个地点所需的IP地址数量为4000。

其次，需要确定借用几位主机位来充当子网地址。假设借用n位主机位，则可以划分出2^{n个子网。同时，每个子网可以容纳2}(16-n)-2台主机（其中2台主机用于表示网络地址和广播地址）。

我们需要使得能分配的子网数最多，因此需要选择尽可能少的主机位来充当子网地址。同时，每个子网里面的主机数也要能容纳一个地点的所有主机。因此，我们可以列出如下的表格：

主机位	子网数	每个子网可容纳的主机数	每个地点所需的IP地址数量	是否满足需求
14	4	16382	4000	否
15	8	8190	4000	否
16	16	4094	4000	是

因此，我们需要借用2位主机位来充当子网地址，选择的子网掩码为255.255.192.0。这种情况下，可以划分出16个子网，每个子网可以容纳4094台主机。

做错啦，正确答案如下
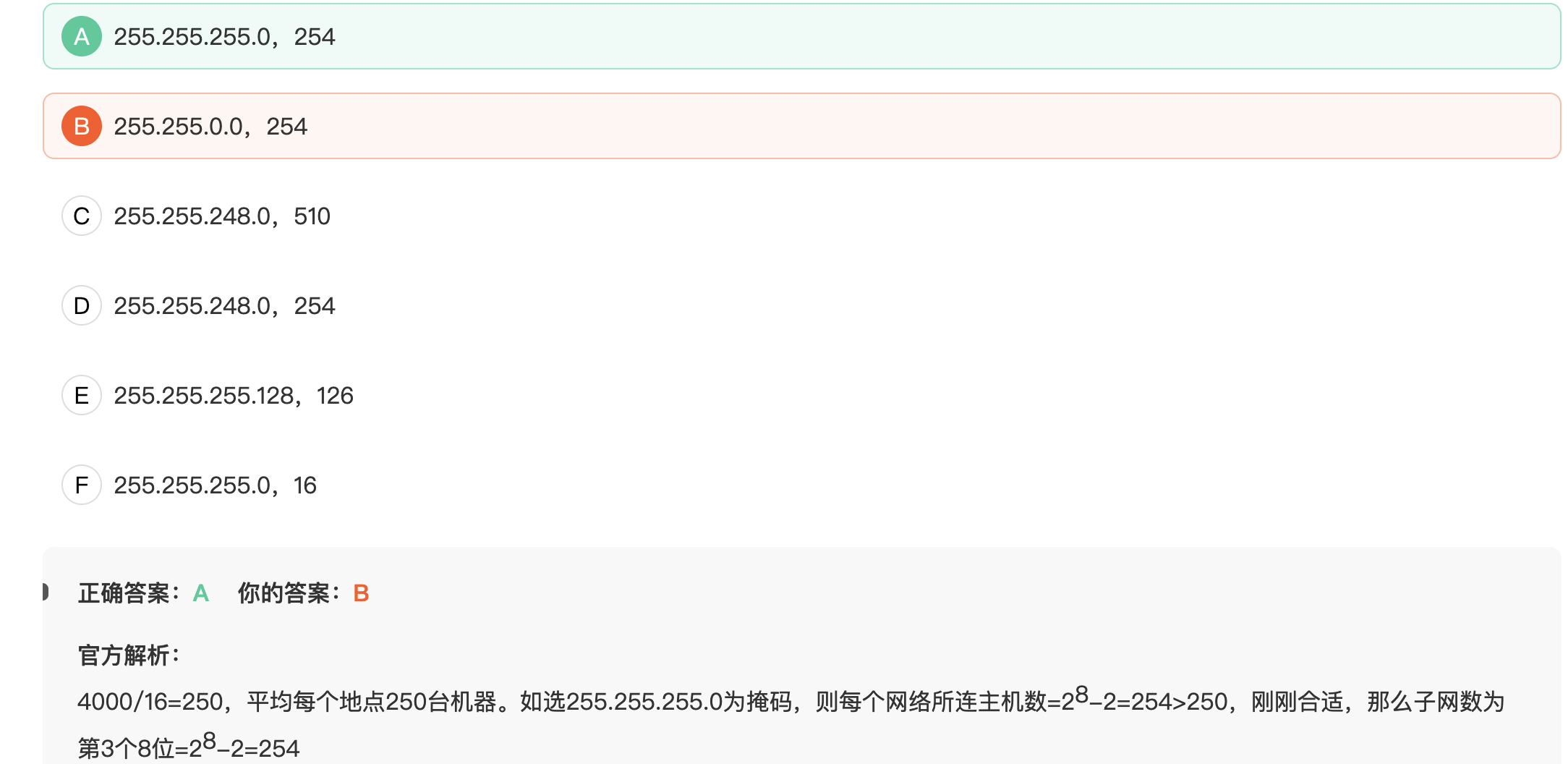
在这里插入图片描述

3.对于下列关键字序列，不可能构成某二叉排序树中一条查找路径的序列是？

一个二叉排序树的查找路径就是从根节点到目标节点的路径，因此不可能构成一条查找路径的序列指的是一个序列无法成为该二叉排序树中任意一个节点的查找路径。

判断一个序列是否可以成为某个二叉排序树中的查找路径，需要满足以下条件：

序列中的第一个元素是根节点；
对于序列中的任意一个元素，其前面的元素都小于它，后面的元素都大于它。

因此，如果一个序列不可能构成某个二叉排序树中的查找路径，则必然存在上述条件不满足。可以通过遍历这个序列来检查这两个条件是否被满足，如果不满足则说明这个序列不可能是任何一个二叉排序树中的查找路径。

4.如下代码：请问m为什么值时能使程序输出default？

public class Test1 {
  public static void main(String args[]) {
    int m;
    //这里设置m的值
    switch (m) {
      case 0: System.out.println("case 0");
      case 1: System.out.println("case 1"); break;
      case 2:
      default: System.out.println("default");
    }
  }
}

在这里插入图片描述
在这段代码中，变量m没有被初始化，因此它的值是不确定的。在Java中，如果一个变量没有被初始化，那么它就会被赋予一个默认值，int类型的默认值为0。

根据switch语句的规则，如果m的值匹配不到任何一个case语句，那么就会执行default语句。因此，只有当m的值不是0或1或2时，才会输出default。因此，m的值必须是除了0、1、2以外的其他值，才能使程序输出default。

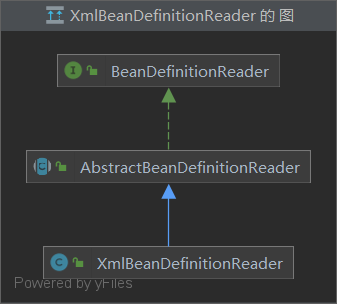
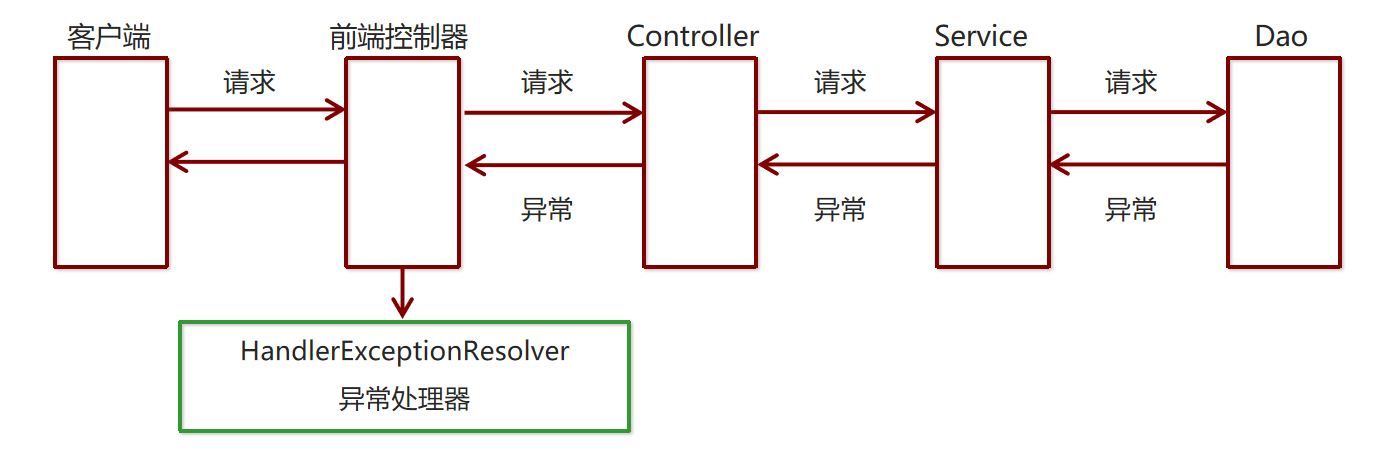
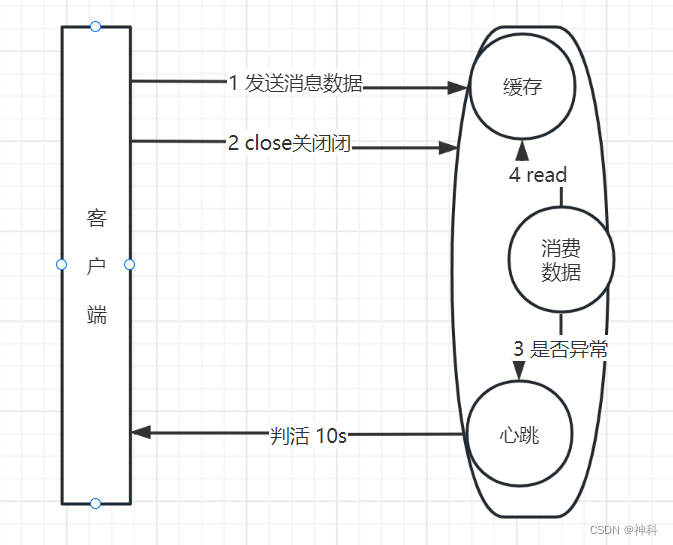
5.下图是哪种UML图？

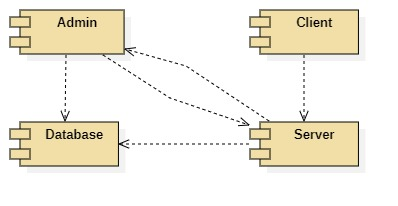
在这里插入图片描述

6. 在数据库一个事务执行的过程中，此事务所访问的数据被其他的事务访问并且修改，致使第一个事务处理的结果异常，这个想象违背了事务的

在这里插入图片描述
在数据库中，事务必须满足ACID四个特性：原子性（Atomicity）、一致性（Consistency）、隔离性（Isolation）和持久性（Durability）。

根据题目描述，第一个事务执行过程中所访问的数据被其他事务访问并修改，导致第一个事务处理结果异常。这个情况违背了事务的一致性，因为事务应该保证其操作能够将数据库从一个一致性状态转换到另一个一致性状态。

因此，答案是B一致性。

错了，不太明白
在这里插入图片描述

7. 下列关于linux查看进程命令说法错误的是？

A、ps -aux可查看运行中的进程
B、ps -ef可查看运行中的进程
C、"pstree -p 进程ID"可查看主线程和子线程之间的关系
D、"ps -aL | grep 进程名"不能查看主线程有哪些子线程
E、ps命令不能动态的显示进程信息
在这里插入图片描述
选项 D 中的说法是错误的。

ps -aL | grep 进程名是查看指定进程及其子线程的命令，而不是不能查看主线程有哪些子线程。该命令会显示所有包括线程在内的进程信息，并可以通过管道符和grep命令过滤出需要的信息。

因此，选项D是错误的。其他选项中，A、B、C、E 的说法都是正确的。

8. 设 N 是描述问题规模的非负整数(N非常大)，下面程序片段的时间复杂度最接近于?

x=4；
while(x<=n/2)
 x=4*x；

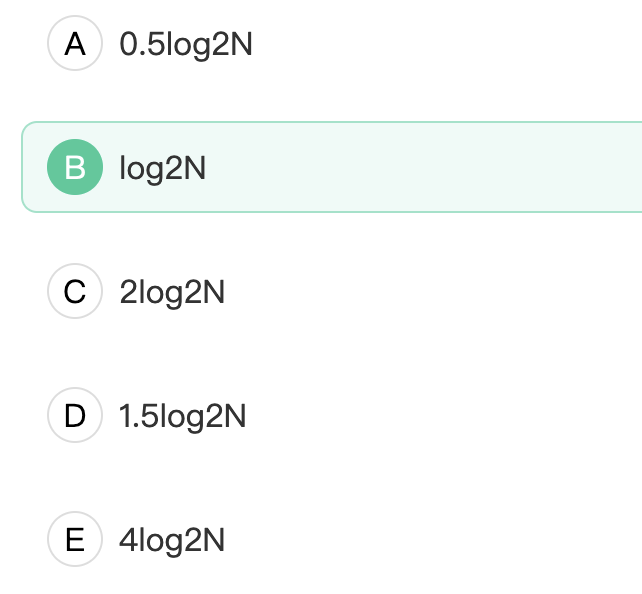
在这里插入图片描述

在这段程序中，x 的值每次乘以 4，直到大于 n/2。设 x 在第 k 次迭代后的值大于 n/2，即 4^k > n/2，则有：

4^k > n/2
2^2k > n/2
2^(2k+1) > n

因此，在最坏情况下，x 可能增长到 n 的对数级别。时间复杂度是 O(logn)。

因为这个问题规模 N 非常大，并且没有其他操作来增加时间复杂度，所以可以忽略除了 while 循环外的代码。因此，该程序片段的时间复杂度最接近于 O(logN)。

在这里插入图片描述

9. 全球化项目测试中，下列哪项描述是不正确的？

A、日期跟时间的格式，包含各式日历
B、书写方向大家都是由左到右，只需要各国语言是否会因文字太长造成位置错乱即可。
C、政府给定的编码需要单独测试: 如身份证号码，美国的社会安全码等
D、电话号码、地址和国际邮递区号。
在这里插入图片描述

10. 对 n 个互不相同的符号进行哈夫曼编码。若生成的哈夫曼树共有 35 个结点，则 n 的值是：

在这里插入图片描述
哈夫曼编码是一种可变长度编码，用于将字符集中的字符映射为二进制编码。哈夫曼树是一种用于构建哈夫曼编码的二叉树。

对于 n 个互不相同的符号进行哈夫曼编码，生成的哈夫曼树共有 2n-1 个结点。因此，根据题意可得：

2n-1 = 35

解得：

n = (35+1)/2 = 18

因此，n 的值是 18。

11. 已知某路由器的路由表如下：

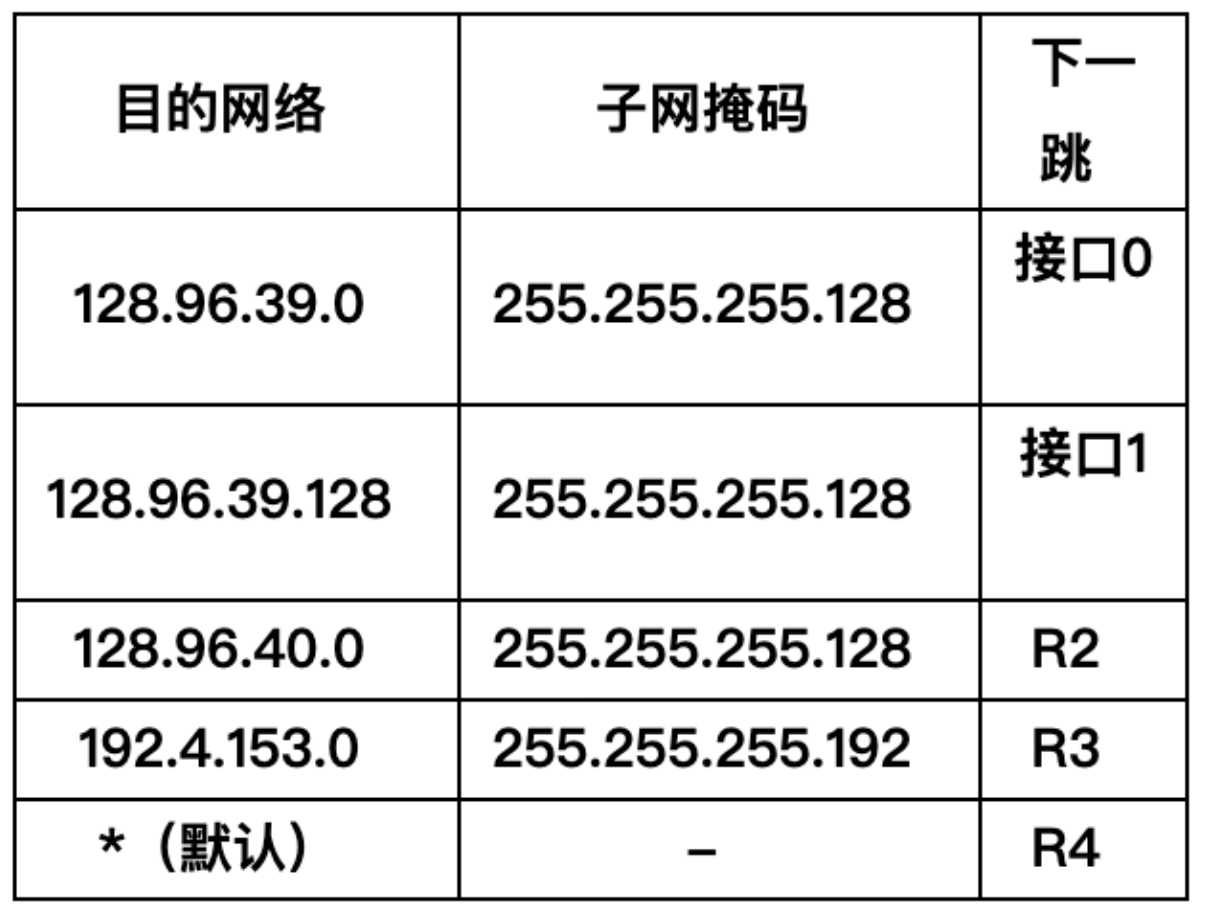
在这里插入图片描述

现共收到2个分组，其目的IP地址分别为：
（1）128.96.39.9
（2）192.4.153.90
那么它们2个分组的下一跳分别为:
在这里插入图片描述

根据路由表可得：

目的地址	子网掩码	下一跳
128.96.39.0	255.255.255.0	192.4.153.254
192.4.153.0	255.255.255.0	192.4.153.253
默认	0.0.0.0	192.4.153.249

对于目的 IP 地址为 128.96.39.9 的分组，其与目的地址 128.96.39.0 在同一个子网，因此下一跳为 192.4.153.254。

对于目的 IP 地址为 192.4.153.90 的分组，其与目的地址 192.4.153.0 在同一个子网，因此下一跳为 192.4.153.253。

因此，它们两个分组的下一跳分别为 192.4.153.254 和 192.4.153.253。

12. 中兴经常会举办各种比赛，假设现在有一张表contestInfo(student_id, contest_id), 其中student_id表示学生id，contest_id表示比赛的id，如果想要知道每个学生参加了中兴举办了多少次比赛，那么可以使用以下哪个sql语句实现?

A、select student_id, sum(contest_id) from contestInfo ;
B、select student_id, sum(contest_id) from contestInfo group by student_id;
C、select student_id, count(contest_id) from contestInfo;
D、select student_id, count(contest_id) from contestInfo group by student_id;
E、select student_id, max(contest_id) from contestInfo;
F、select student_id, max(contest_id) from contestInfo group by student_id;

在这里插入图片描述
正确的 SQL 语句是选项 D。

select student_id, count(contest_id) from contestInfo group by student_id;

这条语句中，count(contest_id) 统计了每个学生参加比赛的次数，group by student_id 对结果按照学生分组，最终输出每个学生参加比赛的次数。

因此，选项 D 是正确的。

13. 集成测试中发现的缺陷不包含以下哪一类？

A、单元传送了错误的数据，或没有传送数据，导致接收数据的单元不能操作或崩溃
B、错误的变量初始化或默认值。
C、通信正常，但是被调用的单元使用不同的方法来解析接收到的数据
D、数据内容传输正确，但是传输的时间错误、传输的延迟

在这里插入图片描述
集成测试主要是测试系统或软件模块之间的交互和协作。根据这个定义，选项 D 不属于集成测试中发现的缺陷。

因此，选项 D 是正确答案。选项 A、B 和 C 属于集成测试中可能出现的缺陷类型，分别是数据传输错误、变量初始化或默认值错误以及通信协议不一致。
在这里插入图片描述

14. 相对普通系统的测试而言，综合系统的测试具有如下额外的特征：

A、多层次的集成和版本管理。
B、测试的持续周期短。
C、各个组件的开发不同步以及大量回归测试需求。
D、由于更换或更新个别过时的组件而需要进行维护测试。
在这里插入图片描述

综合系统测试具有如下额外的特征：

A. 多层次的集成和版本管理：综合系统由多个子系统或模块组成，需要进行多层次的集成测试，并且需要进行版本管理来保证各个组件之间的协调和兼容性。

B. 测试的持续周期短：相对于普通系统测试而言，综合系统的测试周期更长，因为其包含的功能更多、更复杂，需要进行更多的测试和验证。

C. 各个组件的开发不同步以及大量回归测试需求：综合系统的各个组件可能由不同的开发团队开发，在集成过程中容易出现不同步的情况，这就需要进行大量的回归测试来确保修改一个组件不会影响其他组件的正常运行。

D. 由于更换或更新个别过时的组件而需要进行维护测试：随着时间的推移，某些组件可能会变得过时或不再适用，需要进行更换或更新。这就需要进行维护测试来确保更换或更新后的组件与其他组件的兼容性和稳定性。

因此，选项 A、C 和 D 是正确答案。

(多选)15. 设某公司校招的时候收到简历的男女比例为3:1，男性中投递算法工程师的岗位的占男性投递岗位的40%，女性中投递算法工程师的岗位的占女性投递岗位的20%，HR随机抽取发现一份简历标题是算法工程师，问这份简历是属于男性的概率是多少?

在这里插入图片描述
设总投递简历数为 4x（其中男性投递的简历数为 3x，女性投递的简历数为 x），男性投递算法工程师岗位的简历数为 0.4 * 3x = 1.2x，女性投递算法工程师岗位的简历数为 0.2 * x = 0.2x。

因此，投递算法工程师岗位的总简历数为 1.2x + 0.2x = 1.4x，其中男性占比为 1.2x / 1.4x = 6 / 7，女性占比为 0.2x / 1.4x = 1 / 7。

从中随机抽取一份标题为算法工程师的简历，属于男性的概率为 6 / 7，因此选项 B是正确答案。

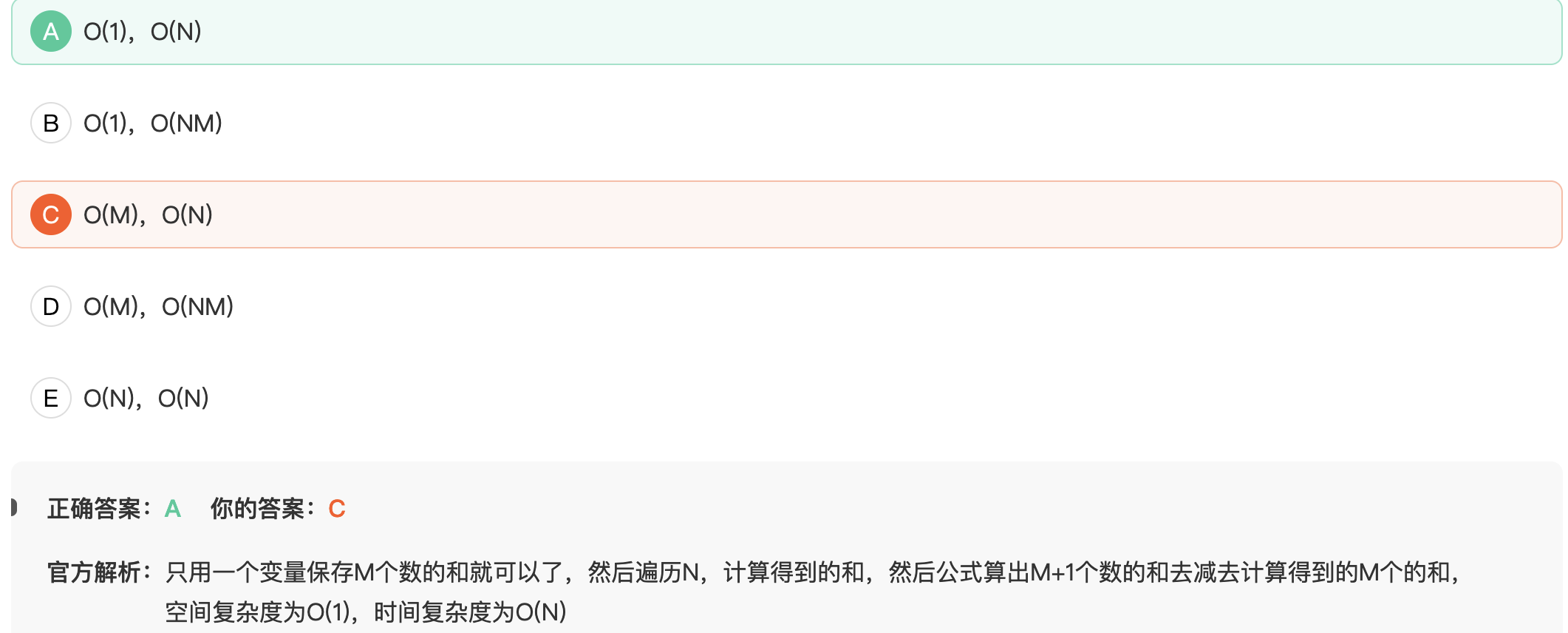
16. 给定一个含 N(N≥1)个整数的数组(N无重复的元素)，N数组元素一定包含M(1<=M<=N)个正整数，M中每个数的范围都在[1,M+1]。请找出M中未出现的1个最小正整数(一定存在且只有1个)。例如：数组N为{-5, 3, 2, 4}时，M为{3,2,4}，M中每个数的范围都在[1,4]，其中M中未出现的最小正整数是 1；数组N为{-5, 3, 1, 4}时，M为{3,1,4}，M中每个数的范围都在[1,4]，其中M中未出现的最小正整数是 2；数组N为{1, 2, 3}时，M为{1,2,3}，M中每个数的范围都在[1,4]，其中M中未出现的最小正整数是 4。如果是在空间复杂度最优为_的情况下，时间复杂度最优为_？

在这里插入图片描述
在空间复杂度最优的情况下，可以使用数组本身来记录 M 中每个数是否出现过。具体地，可以将 M 中每个数减去 1 后作为数组下标，然后将对应位置上的数取相反数，表示该数已经出现过。最后遍历一遍数组，找到第一个正数的下标即可。

时间复杂度最优的情况是 O(N)，因为需要遍历一遍数组 N。空间复杂度最优的情况是 O(M)，因为只需要一个长度为 M 的数组来记录 M 中的元素是否出现过。
在这里插入图片描述

17. 某操作系统中，页面大小为4k，分配给每个进程的物理页面数为1。在一个进程中，定义了如下二位数组int A[512][512]，该数组按行存放在内存中，每个元素占8个字节。有如下编程方法：

for (int i = 0; i < 512; i++)
{
    for (int j = 0; j < 512; j++)
    {
        A[i][j] = 0;
    }
}

那么以上程序运行产生的缺页次数为?

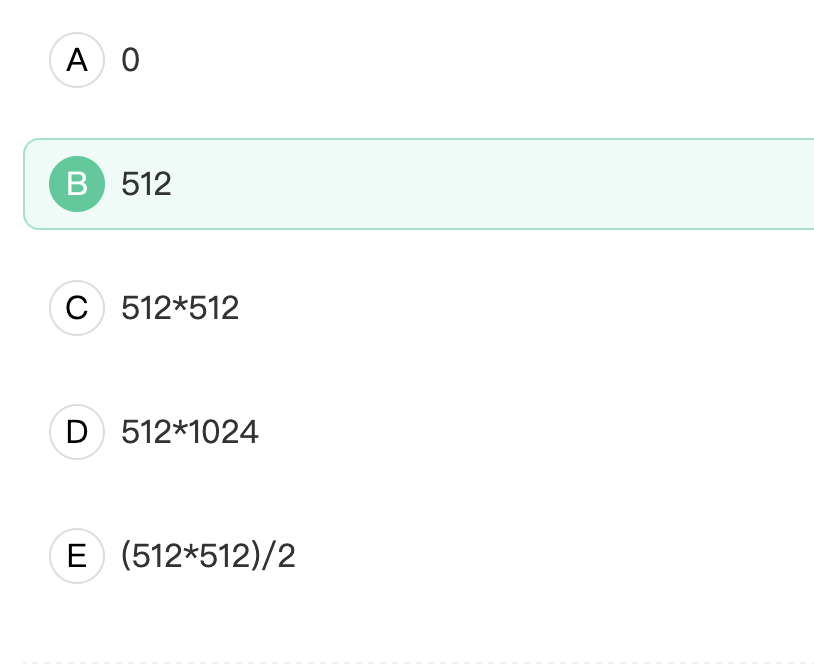
在这里插入图片描述
该二维数组中有 512*512=262144 个元素，每个元素占 8 个字节，因此总共需要的内存空间为：

262144 * 8 = 2097152 字节 = 2048 KB

由于页面大小为 4 KB，所以需要分配的物理页面数为：

2048 / 4 = 512 页

对于二维数组 A，我们可以将其看作由 512 个一维数组组成，每个一维数组有 512 个元素。在对数组进行初始化的过程中，会依次访问每个元素，从而逐个加载页面。由于每个进程只分配了一个物理页面，因此当访问第二个页面时就会发生缺页异常。因此，这段程序运行产生的缺页次数为 511。

已知某个主机捕获的IP分组如下，已知1字节等于8bit，请问该IP分组的源IP地址以及TCP的序号是?（H代表16进制)

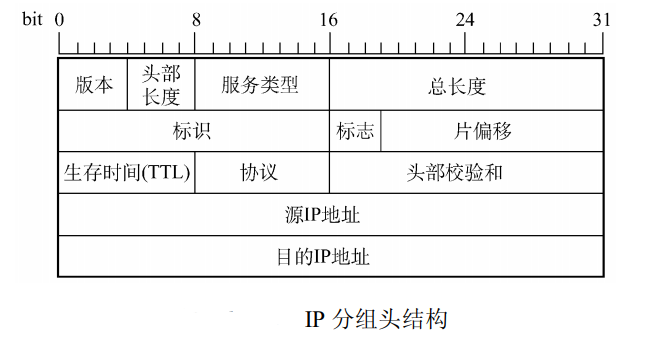
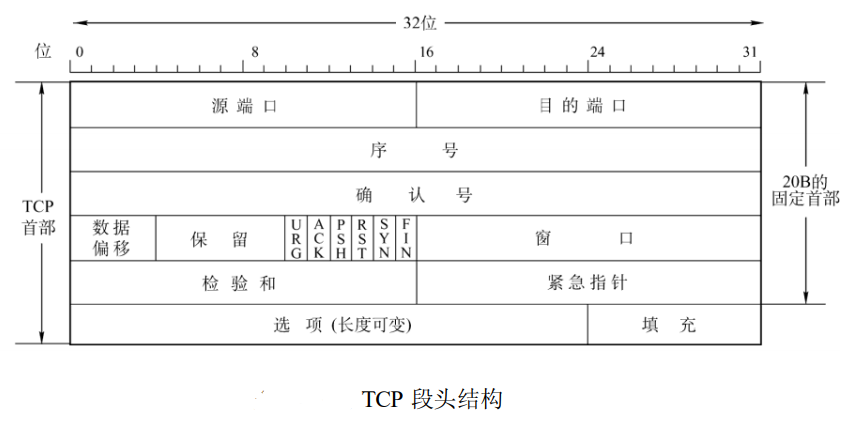
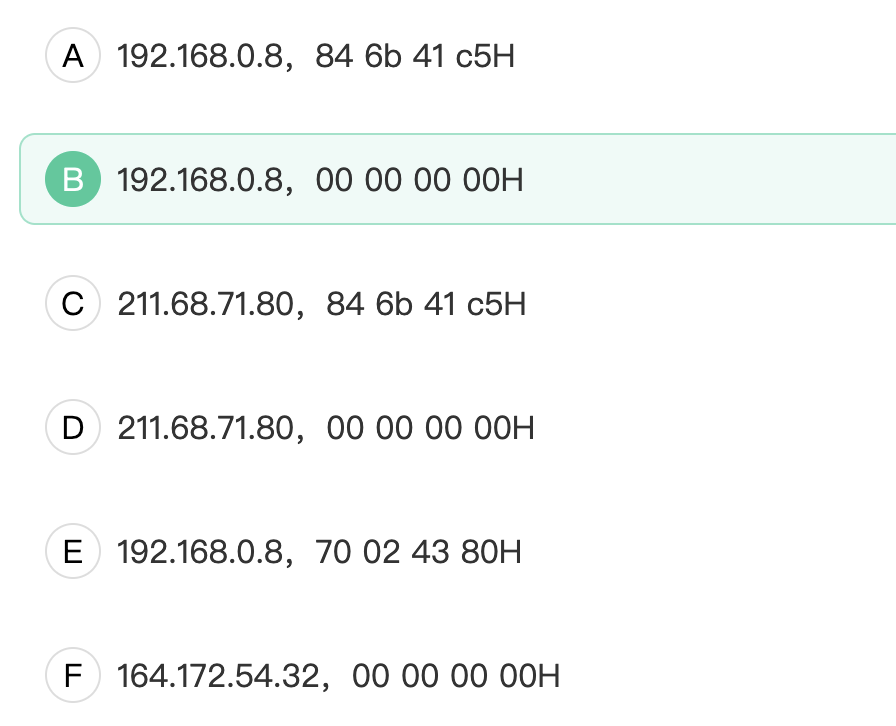
在这里插入图片描述

参考数据：

在这里插入图片描述

根据 IP 分组的格式，可以将前 40 字节内容分为如下几部分：

版本号和首部长度：01 96
区分服务：40
总长度：00 d3
标识符：44 47
标志位和片偏移：50 45
生存时间：00
协议：06
首部校验和：1d e8
源 IP 地址：c0 a8 00 08
目标 IP 地址：0b d9 13 88
TCP 报文（后续部分）

因此，该 IP 分组的源 IP 地址为：192.168.0.8，目标 IP 地址为：11.217.19.136。至于 TCP 报文的具体内容，则需要查看后续部分的数据。
在这里插入图片描述

19. std::function是一种C++11的新特性。是可调用对象的包装器，是一个类模板，它可以统一处理函数，函数对象，函数指针，并允许保存和延迟执行它们。std::function<A(B)> func;其中A表示接受函数的返回值，B表示参数，那么依次推测如下代码中哪几行添加是对的?

#include <iostream>
#include <functional>
#include <string>
#include <vector>
typedef std::function<int(int, std::string)> testFuncCallback;
void func1(int a, std::string b)
{
}
int func2(int a, std::string b)
{
    return 0;
}
int func3(std::string a, int b)
{
    return 0;
}
int func4(int a, int b, std::string c)
{
    return 0;
}
std::string func5(int a, int b)
{
    return "";
}
int main(void)
{
    std::vector<testFuncCallback> testFuncCallbackVec;
    testFuncCallbackVec.push_back(func1);//1
    testFuncCallbackVec.push_back(func2);//2
    testFuncCallbackVec.push_back(func3);//3
    testFuncCallbackVec.push_back(func4);//4
    testFuncCallbackVec.push_back(func5);//5
    return 0;
}

在这里插入图片描述代码中第 1、2、4 行是对的，可以添加到 vector 中。第 3、5 行不对，无法转换成 std::function<int(int, std::string)> 类型。

原因如下：

第 1 行：func1 是一个函数，虽然没有返回值，但其参数类型与 std::function<int(int, std::string)> 相符合，可以将其转换成 std::function<int(int, std::string)> 类型。
第 2 行：func2 是一个有返回值的函数，其返回值类型为 int，且参数类型与 std::function<int(int, std::string)> 相符合，可以将其转换成 std::function<int(int, std::string)> 类型。
第 3 行：func3 的返回值类型为 int，而不是 std::string，因此无法将其转换成 std::function<int(int, std::string)> 类型。
第 4 行：func4 的参数类型与 std::function<int(int, std::string)> 不完全相符，因为其包含了一个额外的参数 std::string c，因此无法将其转换成 std::function<int(int, std::string)> 类型。
第 5 行：func5 的返回值类型为 std::string，而不是 int，因此无法将其转换成 std::function<int(int, std::string)> 类型。

因此，正确的代码应该是：

#include <iostream>
#include <functional>
#include <string>
#include <vector>

typedef std::function<int(int, std::string)> testFuncCallback;

void func1(int a, std::string b)
{
}

int func2(int a, std::string b)
{
    return 0;
}

int func4(int a, int b, std::string c)
{
    return 0;
}

int main(void)
{
    std::vector<testFuncCallback> testFuncCallbackVec;
    testFuncCallbackVec.push_back(func1);
    testFuncCallbackVec.push_back(func2);
    testFuncCallbackVec.push_back(func4);
    return 0;
}

在这里插入图片描述

20. 在排序中，对尚未确定最终位置的所有元素进行一遍处理称为一趟排序。下列排序方法中，哪个排序算法不能在每一趟排序结束能够确定一个元素最终位置？

B 冒泡排序不能在每一趟排序结束时确定一个元素最终位置。

冒泡排序是通过比较相邻两个元素的大小，将大的元素逐步“冒泡”到数组的尾部。在每一趟排序中，只有最后一次交换的位置之后的元素才已经排好序，而前面的元素仍然可能发生交换。因此，冒泡排序无法在每一趟排序结束时确定一个元素最终位置。

而其他几种排序算法都可以在每一趟排序结束时确定一个元素最终位置：

简单选择排序：每次在未排序的部分中选择最小的元素，放到已排序的部分的末尾，因此每次排序能够确定一个元素的最终位置。
希尔排序：通过跨越多个元素进行插入排序，每次排序可以确定多个元素的最终位置。
快速排序：通过选取一个基准元素，并将小于等于该元素的元素放在它左边，大于该元素的元素放在它右边，将数组划分成两个部分。因此每次排序可以确定一个元素的最终位置。
堆排序：通过将待排序的数组构造成一个堆（例如最大堆），将堆顶元素取出并放到已排序的部分的末尾，然后重新调整堆，每次排序可以确定一个元素的最终位置。

因此，选项 B 是正确答案。
在这里插入图片描述

21. 消灭怪物现在有一个打怪类型的游戏，这个游戏是这样的，你有nn个技能，每一个技能会有一个伤害，同时若怪物低于一定的血量，则该技能可能造成双倍伤害，每一个技能最多只能释放一次，已知怪物有mm点血量，现在想问你最少用几个技能能消灭掉他（血量小于等于00）。时间限制：C/C++ 3秒，其他语言6秒空间限制：C/C++ 256M，其他语言512M

输入描述：

第一行输入一个整数，代表有组测试数据。

对于每一组测试数据，一行输入个整数和，代表有个技能，怪物有点血量。

接下来行，每一行输入两个数和，代表该技能造成的伤害和怪物血量小于等于的时候该技能会造成双倍伤害

输出描述：

对于每一组数据，输出一行，代表使用的最少技能数量，若无法消灭输出-1。

示例1
输入例子：

3
3 100
10 20
45 89
5 40
3 100
10 20
45 90
5 40
3 100
10 20
45 84
5 40

输出例子：

3
2
-1

例子说明：

总共3组数据
对于第一组：我们首先用技能1，此时怪物血量剩余90，然后使用技能3，此时怪物剩余血量为85，最后用技能2，由于技能2在怪物血量小于89的时候双倍伤害，故此时怪物已经消灭，答案为3
对于第二组：我们首先用技能1，此时怪物血量剩余90，然后用技能2，由于技能2在怪物血量小于90的时候双倍伤害，故此时怪物已经消灭，答案为2
对于第三组：我们首先用技能1，此时怪物血量剩余90，然后使用技能3，此时怪物剩余血量为85，最后用技能2，由于技能2在怪物血量小于84的时候双倍伤害，故此时怪物无法消灭，输出-1

这道题可以用贪心算法解决。

具体思路：

将所有技能按照伤害从大到小排序。
从技能列表中依次选取技能，如果当前怪物的血量可以被这个技能消灭，则将这个技能加入已选技能列表，并将怪物的血量设为0；否则继续考虑下一个技能。
如果所有的技能都不能消灭怪物，则说明无法消灭，输出-1。

时间复杂度：排序的时间复杂度为 O(nlogn)，每次遍历的时间复杂度为 O(n)，因此总的时间复杂度为 O(nlogn)。

#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

struct Skill {
    int damage;
    int threshold;
};

bool cmp(const Skill& s1, const Skill& s2) {
    return s1.damage > s2.damage;
}

int main() {
    int t;
    cin >> t;
    while (t--) {
        int n, m;
        cin >> n >> m;
        vector<Skill> skills(n);
        for (int i = 0; i < n; i++) {
            cin >> skills[i].damage >> skills[i].threshold;
        }
        sort(skills.begin(), skills.end(), cmp);
        int cnt = 0, i = 0;
        while (m > 0 && i < n) {
            if (skills[i].threshold >= m) {
                m = 0;
                cnt++;
            } else {
                i++;
            }
        }
        if (m != 0) {
            cout << -1 << endl;
        } else {
            cout << cnt << endl;
        }
    }
    return 0;
}

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 15;

int n, m;
int a[N], b[N];
bool st[N];
int res = N;

void dfs(int u, int hp, int cnt)
{
	if(hp <= 0) {
		res = min(res, cnt);
		return ;
	}
	
	if(u == n + 1) return ;
	
	for(int i = 1; i <= n; i ++)
	{
		if(!st[i])
		{
			st[i] = true;
			if(hp <= b[i]) dfs(u + 1, hp - a[i] * 2, cnt + 1);
			else dfs(u + 1, hp - a[i], cnt + 1);
			st[i] = false;
		}
	}
}

int main()
{
	int T;
	cin >> T;
	while(T --)
	{
		cin >> n >> m;
		for(int i = 1; i <= n; i ++) cin >> a[i] >> b[i];
		
		res = N;
		memset(st, false, sizeof st);
		dfs(0, m, 0);

		if(res == N) puts("-1");
		else cout << res << endl;
	}

	return 0;
}

22. 模仿给定一个长度为NN的正整数数列，其中第ii个数为aiai。你可以进行任意次下述“模仿”操作：选择一个位置i(1≤i<N)i(1≤i<N)，令aiai等于ai+1ai+1。现在你希望最大化这个数列的数字和，同时你需要用尽可能少的操作次数来达成这个目标，那么这个数列的数字和最大是多少？达成这个目标最少的操作次数又是多少？

时间限制：C/C++ 1秒，其他语言2秒
空间限制：C/C++ 256M，其他语言512M
输入描述：

第一行一个正整数。
接下来一行个整数，含义如题面所述。

输出描述：

两个空格分隔的整数，第一个代表这个数列最大的数字和，第二个代表达成这个目标最少的操作次数。

示例1
输入例子：

6
10 3 3 5 3 5

输出例子：

35 3

例子说明：

先选择位置\text 5进行操作，变成10 3 3 5 5 5，再选择位置\text 3进行操作，变成10 3 5 5 5 5，最后选择位置\text 2进行操作，变成10 5 5 5 5 5，数字和最大为35

思路：

对于一个数列而言，我们可以将其分为若干个连续的区间，每个区间内的数相等。因此，我们只需要考虑如何将这些区间扩大成最长的区间，并计算扩大区间所需的操作次数。

具体地，假设当前数列中第 i 个数和第 i+1 个数不相等，则我们需要将第 i 个数增加到第 i+1 个数的值，使得这两个数相等。同时，我们还需要记录下操作次数，统计总共需要的操作次数。

时间复杂度：O(n)，其中 n 是数列的长度。遍历一次数列即可计算出答案。

#include <iostream>
 #include <string>
 #include <stack>
 int main() //单调栈  找到下一个更大的数
 {
     int n;
     std::cin >> n;
     unsigned long long array[n];
     for (int i = 0; i < n; i++) std::cin >> array[i];
     unsigned long long sum = 0;
     unsigned long long count = 0;
     std::stack< unsigned long long> s;
     for (int i = n-1;i>=0;i--){
         while (!s.empty() && array[i] >= s.top())
         {
             s.pop();
         }
         if(!s.empty()){
             count++;
             sum += s.top();
             s.push(s.top());
         }else{
             sum += array[i];
             s.push(array[i]);
         }
     }
     std::cout << sum << " " << count << std::endl;
 
  }