采样方法

11.1 简介

1. 什么是采样

   从一个分布中生成一批服从该分布的样本，该过程叫采样.采样本质上是对随机现象的模拟，根据给定的概率分布，来模拟产生一个对应的随机事件。采样可以让人们对随机事件及其产生过程有更直观的认识.

2. 蒙特卡洛

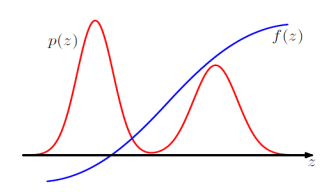
   要解决的问题：寻找某个定义在概率分布𝑝(𝑧)上的函数𝑓(𝑧)的期望，即计算$\mathbb{E}(f)=\int f(\mathbf{z})p(\mathbf{z})\mathrm{d}\mathbf{z}$

   对于大多数实际应用中的概率模型来说，无法精确计算其和或积分，可以采取基于数值采样的近似推断方法，也被称为蒙特卡罗(MonteCarlo)方法

   对这个问题，蒙特卡罗方法是从概率分布𝑝(𝑧)中独立抽取𝑙个样本$z^{(1)},z^{(2)},...,z^{(l)}$ ,这样期望即可通过有限和的方式计算，以此得到一个经验平均值,即计算：$\hat{f}=\frac{1}{L}{\sum }_{l=1}^{L}f\left({\mathbf{z}}^{(l)}\right)$

   

11.2 常见采样方法

11.2.1 均匀分布采样

均匀分布是指整个样本空间中的每一个样本点对应的概率(密度)都是相等的；根据样本空间是否连续，又分为离散均匀分布和连续均匀分布。

一般计算机的程序都是确定性的，无法产生真正意义上的完全均匀分布的随机数，只能产生伪随机数，用线性同余法生成区间[0, m - 1]上的伪随机数序列：
$$x_{t+1}=(a\cdot x_t+c)\mathrm{mod}m$$
其中，模$m>0$,系数$0<a<m$,增量$0\le c<m$，种子$x_0$满足$0\le x_0<m$

11.2.2 逆变换采样

定理：设𝑦是一个连续随机变量，概率密度函数为𝑝(𝑦) ，累计分布函数为ℎ(y) =P(𝑦) ，则𝑧 = ℎ(y) 是定义在区间0 ≤ 𝑧 ≤ 1上的均匀分布，即𝑝 (𝑧) = 1 (0 ≤ 𝑧 ≤ 1)。

证明：ℎ(y) 是累计分布函数，则0 ≤ 𝑧 = ℎ(y) ≤ 1，且ℎ(y)是单调递增函数 , z的累积分布函数：
$$\begin{array}{c}\mathrm{P}(z\le Z)=\mathrm{P}(h(y)\le Z)=\mathrm{P}(y\le h^{-1}(Z))=h(h^{-1}(Z))=Z\\ \\ p(z)=\frac{\mathrm{d}F(Z)}{\mathrm{d}Z}=1(0\le z\le 1)\end{array}$$

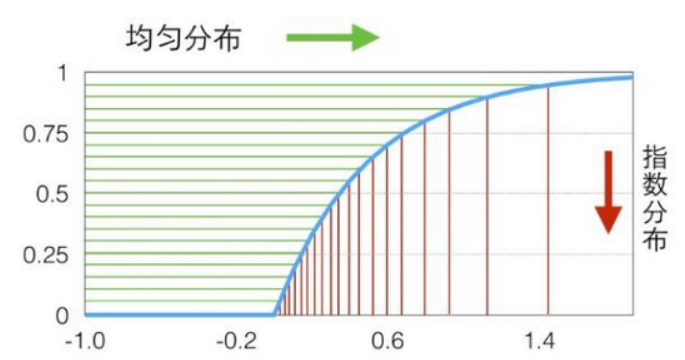
待采样的目标分布为$p(x)$，它的累计分布函数为$\mathrm{z}=\Phi (X)={\int }_{-\infty }^{X}p(x)dx$，则逆变换采样法步骤为：

• 从均匀分布U(0,1)产生一个随机数$z_i$
• 计算逆函数$X_i={\Phi }^{-1}(z_i)$，循环上述步骤，产生更多样本

例:

指数分布密度函数$p(x)=\lambda \exp (-\lambda x)(0\le x<\infty )$其累计分布函数为$\text{z}=\Phi (X)=1-\exp (-\lambda X)$

其逆变换为：$X=-{\lambda }^{-1}\ln (1-z)$

11.2.3 拒绝采样

拒绝采样，又称为接受-拒绝采样，基本思想是用一“更大的的概率分布”或“更简单的概率分布”q(z)覆盖原本的概率分布，这个更简单的概率分布容易采样 (如正态分布)

• $p(z)=\frac{1}{z_p}\tilde{p}(z)$为采样分布，$\tilde{p}(z)$为已知分布，$Z_p$为归一化因子（这一步没看明白暂且当成一样的）
• 引入较简单分布$q(z)$ ，称为提议分布，从中可以较容易采样
• 引入常数k，对任意z满足$\mathrm{kq}(z)\ge \tilde{\mathrm{p}}(z)$，$kq(z)$称为比较函数

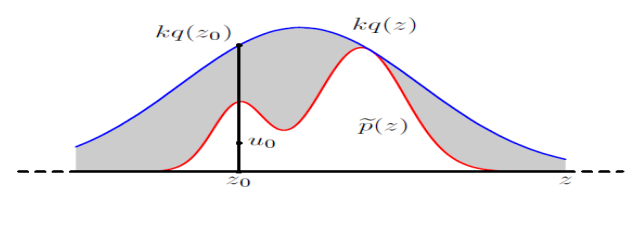
拒绝采样方法的步骤：

• 从$q(z)$中随机采一个样本$z_0$
• 生成区间$[0,kq(z_0)]$上的均匀分布的一个样本$u_0$
• 如果$u_0\ge \tilde{\mathrm{p}}(z)$，则拒绝该样本；反之接受
• 重复以上过程得到$\left[z_0,z_1,\dots z_n\right]$即是对$p(z)$的一个近似

在上述拒绝采样方法中，𝑧的原始值从概率分布𝑞(𝑧)中生成，这些样本之后被接受的可能性为:$\frac{\tilde{p}(z)}{kq(z)}$,因此，样本被接受的平均概率为：
$$p(\mathrm{accept})=\int \left\{\frac{\tilde{p}(z)}{kq(z)}\right\}q(z)dz=\frac{1}{k}\int \tilde{p}(z)dz$$
原则上𝑘可以取得很大，从而满足总能全覆盖，但是不难发现，𝑘取得越大，拒绝概率也更高；因此，选取的𝑘要尽可能的小，并使得𝑘𝑞(𝑧)恰好能覆盖$ \tilde{\mathrm{p}}(z)$

11.2.4 重要采样

$$\begin{gathered} \mathbb{E}[f]=\int f(z)p(z)dz \\ \text{\hspace{1em}(11.1)} \end{gathered}$$

$$\hat{f}=\frac{1}{L}\sum _{l=1}^{L}f(z^{(l)})\text{\hspace{1em}(11.2)}$$

想从复杂概率分布中采样的一个主要原因是能够使用式（11.1）计算期望。重要采样（importance sampling）的方法提供了直接近似期望的框架，但是它本身并没有提供从概率分布$ p(z) $中采样的方法。

公式（11.2）给出的期望的有限和近似依赖于能够从概率分布$p(z)$中采样。然而，假设直接从$p(z)$中采样无法完成，但是对于任意给定的$z$值，我们可以很容易地计算$p(z)$。一种简单的计算期望的方法是将$z$空间离散化为均匀的格点，将被积函数使用求和的方式计算，形式为
$$\mathbb{E}[f]\simeq \sum _{l=1}^{L}p(z^{(l)})f(z^{(l)})$$
这种方法的一个明显的问题是求和式中的项的数量随着$z$的维度指数增长。此外，正如我们已经注意到的那样，我们感兴趣的概率分布通常将它们的大部分质量限制在$z$空间的一个很小的区域，因此均匀地采样非常低效，因为在高维的问题中，只有非常小的一部分样本会对求和式产生巨大的贡献。我们希望从$p(z)$的值较大的区域中采样，或理想情况下，从$p(z)f(z)$的值较大的区域中采样。

与拒绝采样的情形相同，重要采样基于的是对提议分布$q(z)$的使用，我们很容易从提议分布中采样，如下图所示：

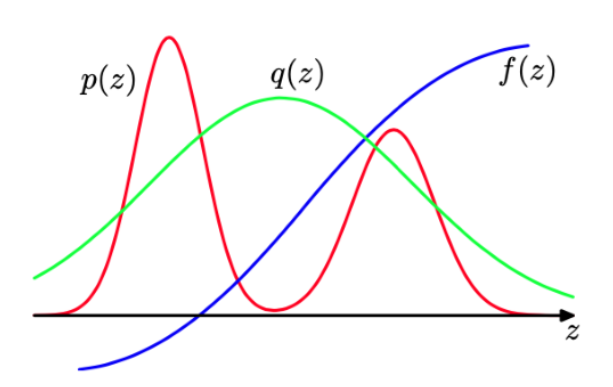
重要采样解决的是计算函数$f(z)$关于分布$p(z)$的期望的问题，其中，从$p(z)$中直接采样比较困难。相反，样本$z^{(l)}$从一个简单的概率分布$q(z)$中抽取，求和式中的对应项的权值为$p(z^{(l)})/q(z^{(l)})$，这样就可以还原到从$p(z)$中取样。

上述过程中的式子，我们可以通过$ q(z) $中的样本$ {z^{(l)}} $的有限和的形式来表示期望
$$\mathbb{E}=\int f(z)p(z)dz=\int f(z)\frac{p(z)}{q(z)}q(z)dz\simeq \frac{1}{L}\sum _{l=1}^L\frac{p(z^{(l)})}{q(z^{(l)})}f(z^{(l)})$$
其中$r_l=p(z^{(l)})/q(z^{(l)})$被称为重要性权重（importance weights），修正了由于从错误的概率分布$q(z)$中采样引入的偏差。

而更常见的情形是，概率分布$p$的计算结果没有标准化，也就是$p(z)=\tilde{p}(z)/Z_p$中我们只知道$\tilde{p}(z)$，其中$\tilde{p}(z)$可以很容易地由$z$计算出来（可能没有函数表达式），而$Z_p$未知（$\tilde{p}(z)$无法积分算）。类似的，我们可能希望使用重要采样分布$q(z)=\tilde{q}(z)/Z_q$中的$\tilde{q}(z)$，它具有相同的性质。于是我们得到:
$$\mathbb{E}[f]=\int f(z)p(z)dz=\frac{Z_q}{Z_p}\int f(z)\frac{\tilde{p}(z)}{\tilde{q}(z)}q(z)dz\simeq \frac{Z_q}{Z_p}\frac{1}{L}\sum _{l=1}^L{\tilde{r}}_{l}f(z^{(l)})$$
其中${\tilde{r}}_l=\tilde{p}(z^{(l)})/\tilde{q}(z^{(l)})$。

我们还可以使用同样的样本集合来计算比值$Z_p/Z_q$，结果为：
$$\frac{Z_p}{Z_q}=\frac{1}{Z_q}\int \tilde{p}(z)dz=\int \frac{\tilde{p}(z)}{\tilde{q}(z)}q(z)dz\simeq \frac{1}{L}\sum _{l=1}^L{\tilde{r}}_l$$

第一个等式中$Z_p$用$\int \tilde{p}(z)dz$等价计算了出来，第二个等式中$Z_q$用$q(z)=\tilde{q}(z)/Z_q$替代

因此：
$$\mathbb{E}[f]\simeq \sum _{l=1}^L{w}_{l}f(z^{(l)})$$
其中:
$$w_l=\frac{{\tilde{r}}_l}{{\sum }_m{\tilde{r}}_m}=\frac{\tilde{p}(z^{(l)})/q(z^{(l)})}{{\sum }_m\tilde{p}(z^{(l)})/q(z^{(l)})}$$

11.2.5 Metropolis方法

与拒绝采样和重要采样相同，我们再一次从提议分布中采样。但是这次我们记录下当前状态$z^{(\tau )}$以及依赖于这个当前状态的提议分布$q(z|z^{\tau })$,从而样本序列$z^{(1)},z^{(2)},\dots$组成了一个马尔科夫链。

我们假设提议分布足够简单很容易直接采样，且$p(\mathbf{z})=\tilde{p}(\mathbf{z})/Z_p$中的$\tilde{p}(\mathbf{z})$可以很容易的计算值。

在算法的每次迭代中，我们从提议分布中生成一个候选样本$z^{\ast }$，然后根据一个恰当的准则接受这个样本。

在基本的 Metropolis 算法中，我们假定提议分布是对称的，即$q(z_A|z_B)=q(z_B|z_A)$对于所有的$z_A$和$z_B$都成立。这样，候选样本被接受的概率为：
$$A({\mathbf{z}}^{\star },{\mathbf{z}}^{(\tau )})=\min \left(1,\frac{\tilde{p}({\mathbf{z}}^{\star })}{\tilde{p}({\mathbf{z}}^{(\tau )})}\right)$$
我们的接受准则是：当接受概率大于预设值u时，则接受这个样本。

如果候选样本被接受，那么$z^{(\tau +1)}=z^{\ast }$;否则候选样本点$z^{\ast }$被抛弃，$z^{(\tau +1)}$被设置为$z^{(\tau )}$

然后从概率分布$q(z|z^{(\tau +1)})$中再次抽取一个候选样本。

可以看到，在 Metropolis 算法中，当一个候选点被拒绝时，前一个样本点会被包含到是最终的样本的列表中，从而产生了这个样本点的多个副本。虽然在实际中我们只会保留一个样本副本，以及一个整数的权因子，记录状态出现了多少次。设计马尔科夫链蒙特卡洛方法的一个中心目标就是避免随机游走行为。

11.2.6 Metropolis-Hasting 算法

与 Metropolis 算法相比，提议分布不再是参数的一个对称函数，此时的接受概率变为：
$$A_k({\mathbf{z}}^{\star },{\mathbf{z}}^{(\tau )})=\min \left(1,\frac{\tilde{p}({\mathbf{z}}^{\star })q_k({\mathbf{z}}^{(\tau )}|{\mathbf{z}}^{\star })}{\tilde{p}({\mathbf{z}}^{(\tau )})q_k({\mathbf{z}}^{\star }|{\mathbf{z}}^{(\tau )})}\right)$$
其中k标记出可能的转移集合中的成员，对于一个对称的提议分布， Metropolis-Hasting 准则会退化为 Metropolis 准则。

具体推导过程设计到马尔科夫链的知识，这里只记形式

11.2.7 吉布斯采样

吉布斯采样是一个简单的并且广泛应用的马尔科夫链蒙特卡洛算法，可以看做 Metropolis-Hasting 算法的一个具体的情形。

考虑我们项采样的概率分布$p(z)=p(z_1,\dots ,z_M)$，并且假设我们已经选择了马尔科夫链的某个初始状态。吉布斯采样的每个步骤涉及到将一个变量的值替换为以剩余变量的值为条件，从这个概率分布中抽取的那个变量的值。具体流程如下：

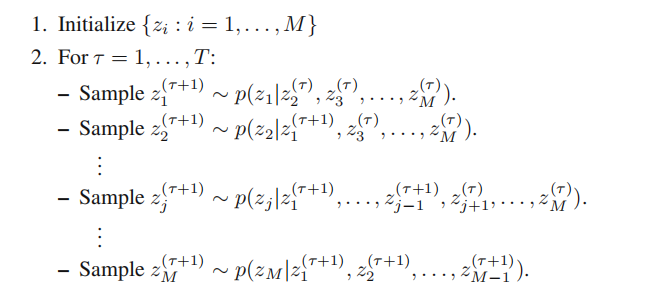
参考书：PRML

参考：PRML学习笔记（十一） - Pelhans 的博客