2023年认证杯SPSSPRO杯数学建模
D题 立体车库的自动调度问题
原题再现:
随着人们生活水平的提高,汽车保有量日益增加,而城市土地资源有限,传统平面停车场土地面积利用率低, 这样便形成了交通拥挤、停车困难的现象。为解决该问题,立体车库应运而生,有效解决了车位难的问题,但是在实际使用过程中,现有的立体车库存在自动化程度低、排队时间长、适应性弱等问题。为了增强其适用性,建筑设计和调度方案等都是值得研究的问题。
我们考虑一种密集排布的立体式车库,这种车库只有一个出口和一个通向出口的通道,为了高效地利用空间,车库的每层只能根据需求预留很少的腾挪空间,这就迫使某些位置的车辆的出库过程需要经历复杂的腾挪过程,所需时间相当可观。为了减少此类问题,这种车库会根据车辆的使用计划自动地移动调整车辆布局。车辆的排列和存放布局对于车辆进出车库的时间有很大影响,特别是遇到更改计划的时候更是如此。例如:车主临时改变行程计划,原定在 30 分钟后使用车辆,改为希望能在 10 分钟后使用车辆,系统如何快速响应需求,进行有效的排队调整,减少车主的等待时间。再比如:车主临时推后行程计划,原来计划在 10 分钟后使用车辆,现在推后到 1 个小时后使用,这种变化又该如何应对?
第一阶段问题:
1. 请结合考虑上面两种情况,提出一个合理的指标体系,用以衡量立体车库在用车计划出现改变时的适应能力;
2. 给出一个立体车库自适应调度的优化算法;
3. 提出一个单出口的立体化车库的布局设计和调度方案。
整体求解过程概述(摘要)
近年来,由于经济的不断增长,人均汽车保有量也随之不断上升,城市停车难的问题愈演愈烈。传统停车模式的缺点也开始展现,而立体车库新技术又面临着诸多瓶颈。为此,如何高效的减少车辆存取等待时长,提高自动化立体车库的自适应能力,寻找最优化的调度方案成了当前备受关注的研究问题。本文通过参考目前主流立体车库发展现状,选择了一种完美符合题目需求的巷道堆垛式立体车库,构建了诸多模型用于衡量立体车库中不同调度方案在不同情况下的自适应能力与需要时长,为其前景发展提供参考,具体研究内容如下:
对于问题一,本文提出以立体车库中存取车辆的排队等候时长作为该指标体系,并且通过建立一个排队论模型以直观的展示整个立体车库的运行模式。本文选用成都市某大型立体车库单位时间段内的存取车辆数据进行取样指标分析,提出假设并使用卡方检验对模型结果进行检验,最终取合适自由度数值计算出假设指标体系的反馈值为最佳。
对于问题二,本文选择将车辆存取所需的总时长设置为目标函数,采用混合改进的GA-SA 算法对于车辆调度分配模型建立求解,并且针对存取用时数据的高低峰期设定不同的存取策略。本文使用 matlab 软件进行优化迭代并作出曲线进行对比分析,最后选择相较之下优化速度提升近的混合改进 GA-SA 算法作为新的优化调度算法。
对于问题三,本文根据实需求构建出了三维物理的巷道堆垛式立体车库模型,并对其进行二维坐标轴化,以此进行调度方案的设计。为了体现方案的优化升级,本文选择建立不同时段不同优先策略的时间消耗模型,使用软件对数据进行绘图分析处理,对传统的单一存取调度方案升级为交叉替换混合方式。本文对比不同优先调度策略的仿真曲线数据图的结果,最后选择了合理的设计布局与最佳的存取车辆调度方案。
问题分析:
(一) 问题 1 的分析
针对问题 1 中要求设计一种能够衡量体现用车计划出现改变时立体车库适应能力的合理指标体系,本文根据目前国内停车市场的紧迫需求,以提高立体车库运营效率为主要目的,并且结合题目中所要求的“单出口、单通道”的“密集排布”立体车库条件,选择以巷道堆垛式立体车库为主要的研究对象,在这基础之上,本文采用用户排队等待的时长用于衡量立体车库的服务效率,以此作为衡量该立体车库在出现关于用车计划改变时适应能力的指标体系,具体通过建立排队论模型,以成都市区某大型立体车库为调查对象,通过真实数据进行模型推演,以验证这一标准体系的合理性。
(二) 问题 2 的分析
针对问题 2 中要求设计一个关于立体车库自适应调度优化算法,首先明确优化方向为提高其自适应调度效率,具体体现该车库存取车辆的策略,此处仍以成都某大型立体车库为数据样本,本文将车俩在立体车库内的总时长设置为目标函数,选择使用一种改进混合的遗传算法与模拟退火算法,通过两者的结合以达到进一步优化升级种群,升级收敛速率,进而达到提高全面搜索水平。其中主要以遗传算法(GA)为基底,将模拟退火算法(SA)作为帮助加入到车库之中。由初始化的种群判断初始温度,并算出车库在整个自适应调度过程中的时间,经过反复迭代升级作图观察其数据是否满足收敛,不断通过交叉,变异选择等操作,进而得到最佳解,并且完成退火过程产生新解,以得到全局最优,结束运行。最后在判断当前该种群内单个个体的算法能否满足收敛条件,若满足就输出最优个体,不满足则循环操作,流程如图。
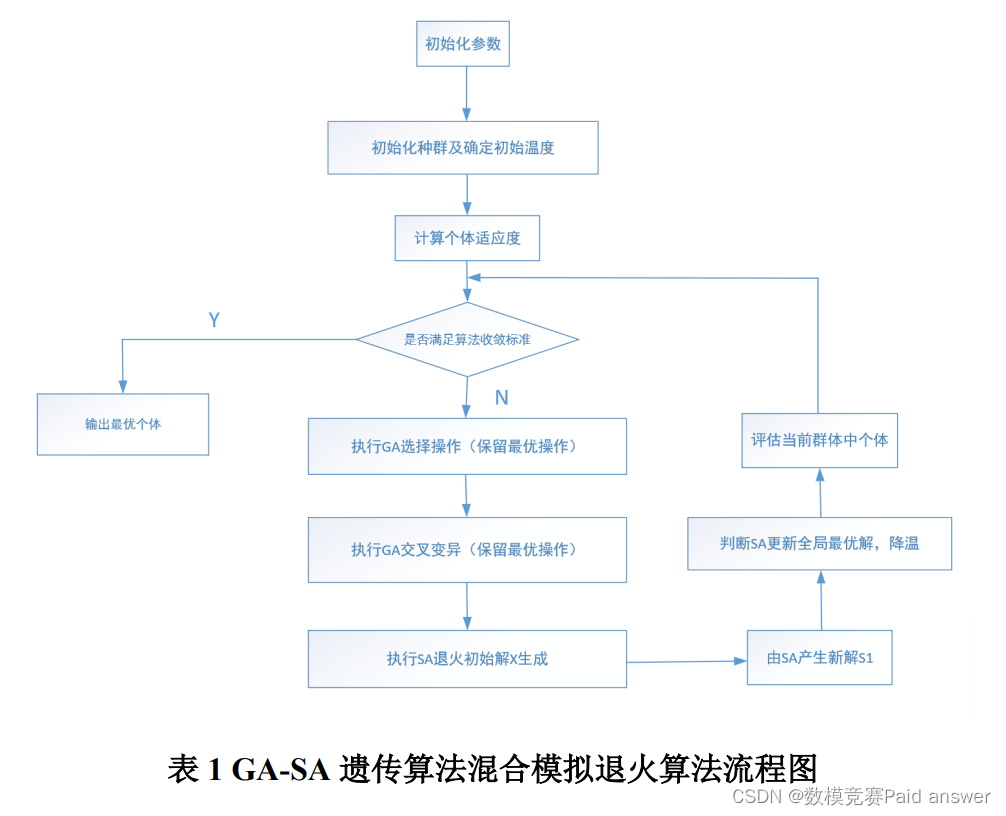
(三) 问题 3 的分析
针对问题 3 要求对该立体车库进行布局设计与新的调度方案的设计,首先明确研究对象仍然选择巷道堆垛式立体车库为目标,并以成都某大型立体车库数据为参考(见附件 1),本文认为一个能够实现高效率存取车辆并具有高适应力的立体车库首先应该体现在存取车辆的方式,因此选择先建立一三维结构的立体车库模型,并且根据不同优先顺序将存取车辆的流程分为了三种,分别是“存车优先”,“取车优先”以及同步进行的“交叉策略”,并跟据参考的实际流程数据进行分时段分高低峰期进行分别讨论验证,建立不同种存取策略的时间消费模型,最终得出最佳布局设计并对堆垛机路径进行优化升级,结合三种存取策略设计出新的最佳方案。
模型假设:
为了使得解答题目过程种得到适当简化,本文做出以下假设用于规范模型算法的合理范围。
假设 1:假设本题中所有的模型合理假设均建立于巷道堆垛式立体车库这一唯一车库类型中。
假设 2:假设本题中选择的某大型立体车库普通存取车辆采样的原始数据不考虑节假日等特殊情况。
假设 3:假设在考虑设计车库的布局与调度方案上不考虑车库本身的运营成本。
假设 4:不考虑机械的使用损耗情况,默认其一直始终保持最佳状态。
完整论文缩略图


全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可
部分程序代码:(代码和文档not free)
% GA-SA 算法实现
% 问题描述:求解最大利润问题
% 输入参数:n=10,m=5,p=1,r=0.9,lambda=1,GA_rate=0.8,SA_rate=0.9,max_iter=1000
% 输出参数:最优解,最大利润
% 初始化种群
pop = rand(n, m);
% 初始化权重向量
w = ones(n, 1);
% 初始化损失函数值
loss = 0;
% 迭代算法
for it = 1:max_iter
% 随机选择一批个体
selected = pop(randperm(n, m), 1);
% 变异
for i = 1:size(selected, 1)
selected(i, :) = randi(size(pop, 1));
end
% 选择父代
parents = selected';
% 计算交叉概率
cross_prob = rbinom(m, 1, GA_rate);
% 进行交叉操作
for i = 1:size(parents, 1)
temp = parents(i, :);
for j = 1:size(parents, 1)
if temp(j) > temp(i)
temp(j) = temp(i);
end
end
parents(i, :) = temp;
end
% 计算交叉后的种群均值
new_pop = [pop(:, 1:m) parents'];
% 计算梯度
descent_vector = zeros(n, 1);
for i = 1:size(new_pop, 1)
descent_vector(i) = -rsqrt(sum(new_pop(i, :) * w' * new_pop(i, :)) /
size(new_pop, 1));
end
% 梯度更新
w = w - descent_vector * rsqrt(sum(descent_vector' * descent_vector) /
size(pop, 1));
% 计算损失函数值
loss = -sum(log(pop(:, 1:m))) / size(pop, 1);
% 输出迭代次数和损失函数值
if mod(it, 100) == 0
fprintf('Iters: %d, Loss: %f\n', it, loss);
end
end
% 输出最优解和最大利润
[~, best_index] = max(pop(:, 1:m));
best = pop(best_index, :);
max_profit = sum(best(:, 1:m)) / size(pop, 1);
fprintf('Best solution: %d %g\n', best_index, best(:, 1));
fprintf('Max profit: %g\n', max_profit);