PAT (甲级) 2022年秋季考试 c++ 满分题解

7-1 Balloon Popping

分数 20

原题

在这里插入图片描述

算法标签

模拟枚举

思路

枚举数组元素，判断每个元素覆盖气球数, 记录最多可覆盖气球数及最多可覆盖气球数开始下标，则最小开始值为最后可覆盖气球位置减高度H

代码

#pragma GCC optimize(2)
#pragma GCC optimize(3)
#include<bits/stdc++.h>
#define int long long
#define rep(i, a, b) for(int i=a; i<b; ++i)
#define Rep(i, a, b) for(int i=a; i>b; --i)
#define x first
#define y second
#define ump unorderer_map
#define pq priority_queue
#define debug(a) cout<<"a = "<<a<<"\n"
#define debugi(a) printf("a = %lld\n", a)
using namespace std;
int n,m, mx=0, mn=1000, MX=1, MXID=0;
int a[100005];
inline int rd(){
	int s=0, w=1;
	char ch=getchar();
	while(ch<'0'||ch>'9'){
		if(ch=='-'){
			w=-1;
		}
		ch=getchar();
	}
	while(ch>='0'&&ch<='9'){
		s=s*10+ch-'0';
		ch=getchar();
	}
	return s*w;
}

signed main(){
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);
	n=rd(), m=rd();
	rep(i, 0, n){
		a[i]=rd();
		mn=min(a[i], mn);
		mx=max(a[i], mx);
	}
	rep(i, 0, n){
		int cnt=1;
		while(a[i]+m>=a[i+cnt]&&i+cnt<n){
				cnt++;
		}
		if(cnt>MX){
			MX=cnt;
			MXID=i;
		}
	}
	if(MXID==a[0]){
		printf("%lld %lld\n", MXID, MX);
	}else if(MXID!=a[0]){
		printf("%lld %lld\n", a[MXID+MX-1]-m, MX);
	}
	return 0;
}

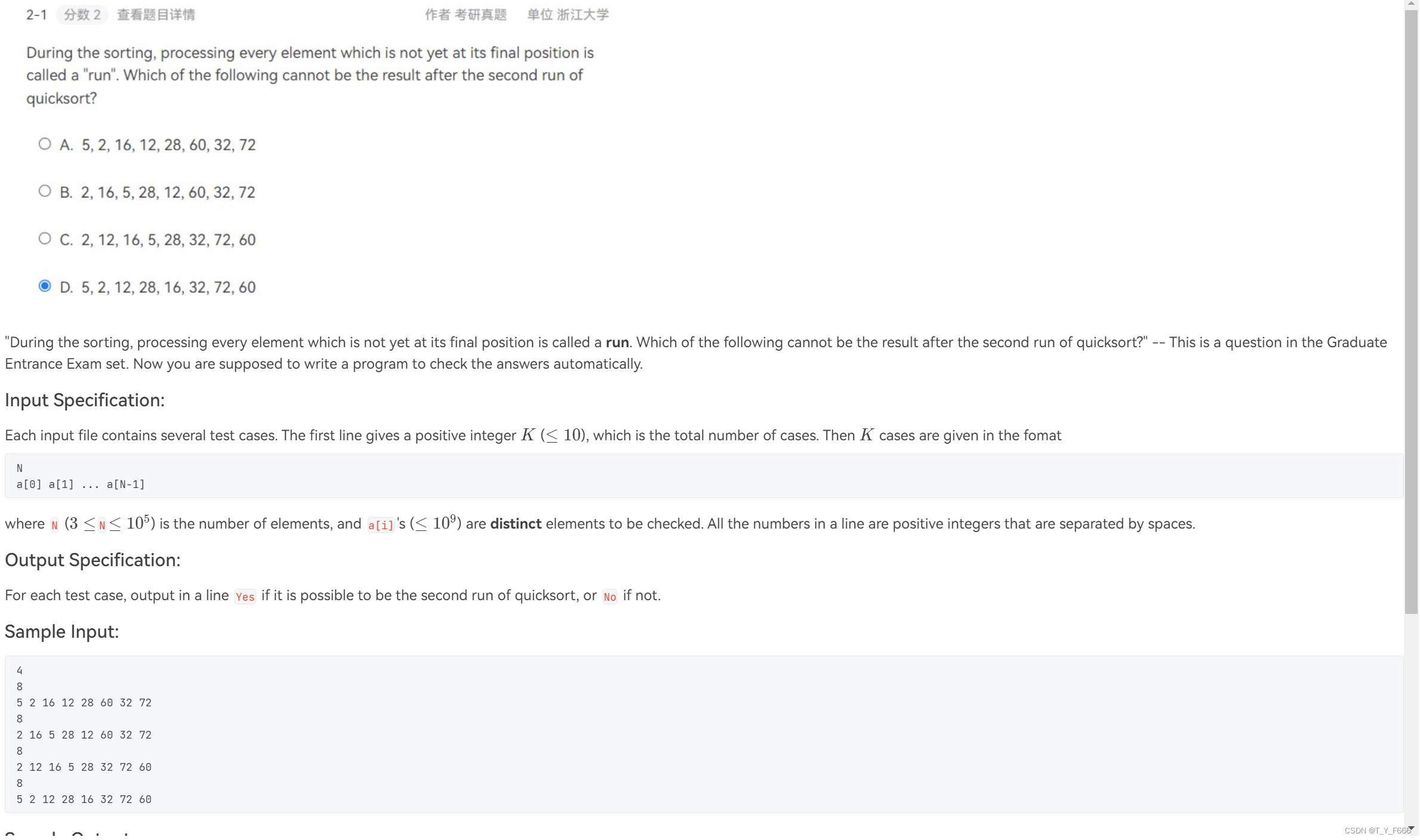
7-2 The Second Run of Quicksort

分数 25

原题

在这里插入图片描述

算法标签

DP 排序

思路

具体思路见第八章动态规划 5 AcWing 1591. 快速排序
值得注意的是，如何通过临界值的数量对结果判断，可分为以下情况
第一轮临界值为a[0]（或a[N]）第一轮临界值为a[N]（或a[0]）临界值的数量2 属于第二轮排序
第一轮临界值为a[0]（或a[N]）第一轮临界值为a[i]（i>0且i<0）临界值的数量2 属于第二轮排序
若不属于上述情况临界值的数量3 属于第二轮排序
否则不属于第二轮排序

代码

#pragma GCC optimize(2)
#pragma GCC optimize(3)
#include<bits/stdc++.h>
#define int long long
#define x first
#define y second
#define ump unordered_map
#define ums unordered_set
#define pq priority_queue
#define rep(i, a, b) for(int i=a;i<b;++i)
#define Rep(i, a, b) for(int i=a;i>=b;--i)
using namespace std;
typedef pair<int, int> PII;
const int N=100005, INF=0x3f3f3f3f3f3f3f3f, MOD=1e9+7;
const double Exp=1e-8;
//int t, n, m, cnt, ans; 
int n, l[N], r[N], a[N];
inline int rd(){
   int s=0,w=1;
   char ch=getchar();
   while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
   while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar();
   return s*w;
}
void put(int x) {
    if(x<0) putchar('-'),x=-x;
    if(x>=10) put(x/10);
    putchar(x%10^48);
}
signed main(){
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);
	int t=rd();
	while(t--){
	    bool flagh=false, flagt=false;
	    vector<int> res;
		n=rd();
		rep(i, 1, n+1){
	    	a[i]=rd();
		}
		rep(i, 1, n+1){
	    	l[i]=max(l[i-1], a[i]);
		}
		r[n+1]=INF;
		Rep(i, n, 0){
	    	r[i]=min(r[i+1], a[i]);
		}
		rep(i, 1, n+1){
	    	if(a[i]>l[i-1]&&a[i]<r[i+1]){
	        	if(i==1){
	            	flagh=true;
	        	}
	        	if(i==n){
	            	flagt=true;
	        	}
	        	res.push_back(a[i]);
	    	}
		}
		if(flagh&&flagt||flagh&&res.size()==2||flagt&&res.size()==2||res.size()==3){
	   		puts("Yes");
		}else{
	   		puts("No");
		}
	}
	return 0;
}

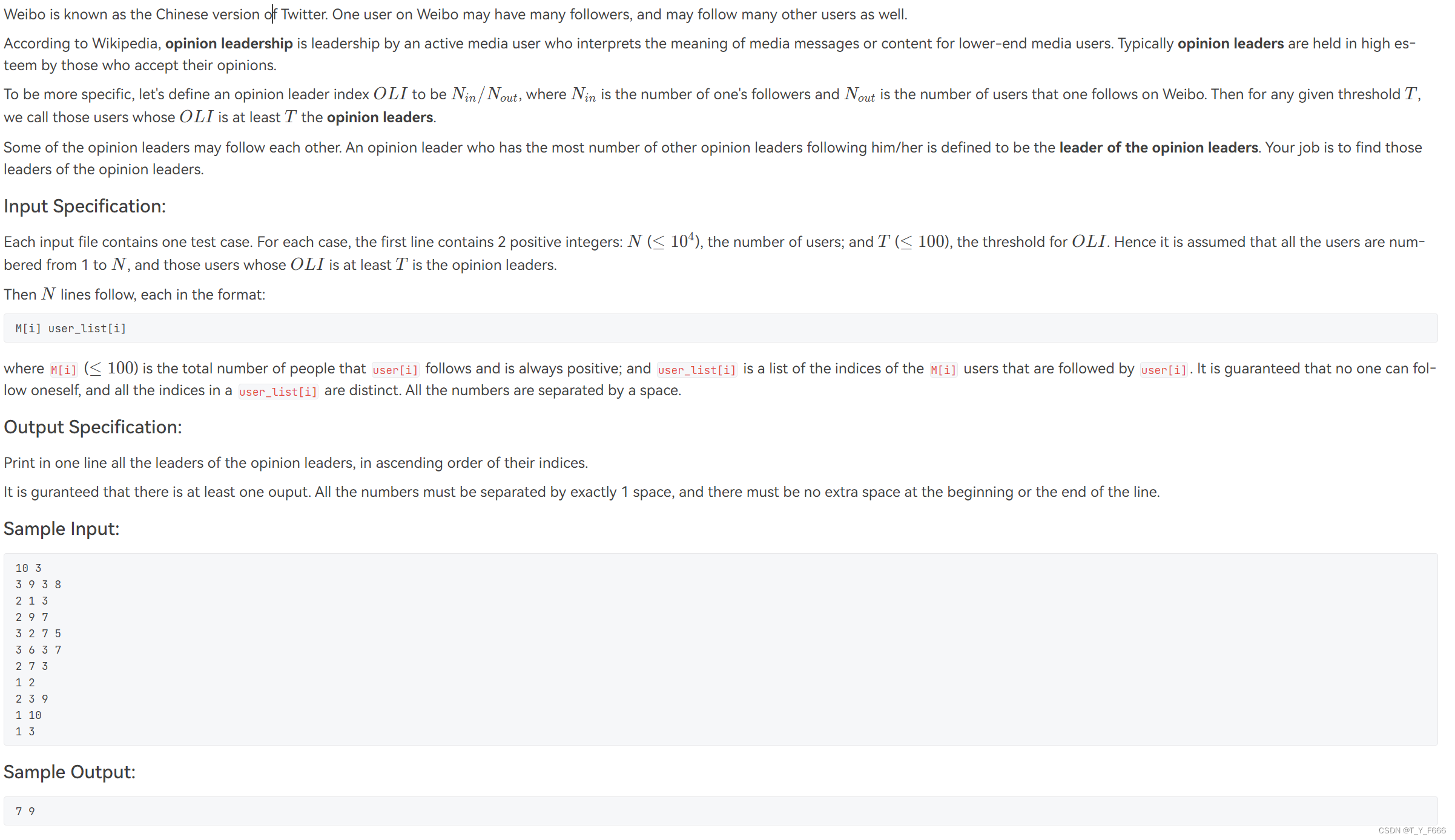
7-3 Leader of the Opinion Leaders

分数 25

原题

在这里插入图片描述

算法标签

图模拟

思路

依题意模拟，具体思路见代码

代码

#pragma GCC optimize(2)
#pragma GCC optimize(3)
#include<bits/stdc++.h>
#define int long long
#define xx first
#define yy second
#define ump unordered_map
#define us unordered_set
#define pb push_back
#define pq priority_queue
#define rep(i, a, b) for(int i=a;i<b;++i)
#define Rep(i, a, b) for(int i=a;i>=b;--i)
using namespace std;
const int N = 10005, inf=0x3f3f3f3f3f3f3f3f, mod=1e9+7;
const double Exp=1e-8;
// in[i] 关注用户i的人 out[i]用户i关注的人
vector<int> in[N], out[N], res;
bool st[N];
inline int rd(){
   int s=0,w=1;
   char ch=getchar();
   while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
   while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar();
   return s*w;
}
void put(int x) {
    if(x<0) putchar('-'),x=-x;
    if(x>=10) put(x/10);
    putchar(x%10^48);
}
signed main(){
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);
	int n=rd(), t=rd();
	rep(i, 1, n+1){
		int x=rd();
		while(x--){
			int y=rd();
			in[y].pb(i);
			out[i].pb(y);
		}
	}
	// 标记精神领袖
	rep(i, 1, n+1){
		if(in[i].size()>=out[i].size()*t){
			st[i]=true;
		}
	}
	int mx=0;
	rep(i, 1, n+1){
		int m=0;
		// 统计粉丝数
		rep(j, 0, in[i].size()){
			if(st[in[i][j]]){
				m++;
			}
		}
		if(st[i]){
			// 更新最大粉丝数 清空原领袖
			if(m>mx){
				mx=m;
				res.clear();
				res.pb(i);
			}else if(m==mx){// 更新领袖
				res.pb(i);
			}
		}
	}
	printf("%lld", res[0]);
	rep(i, 1, res.size()){
		printf(" %lld", res[i]);	
	}
	return 0;
}

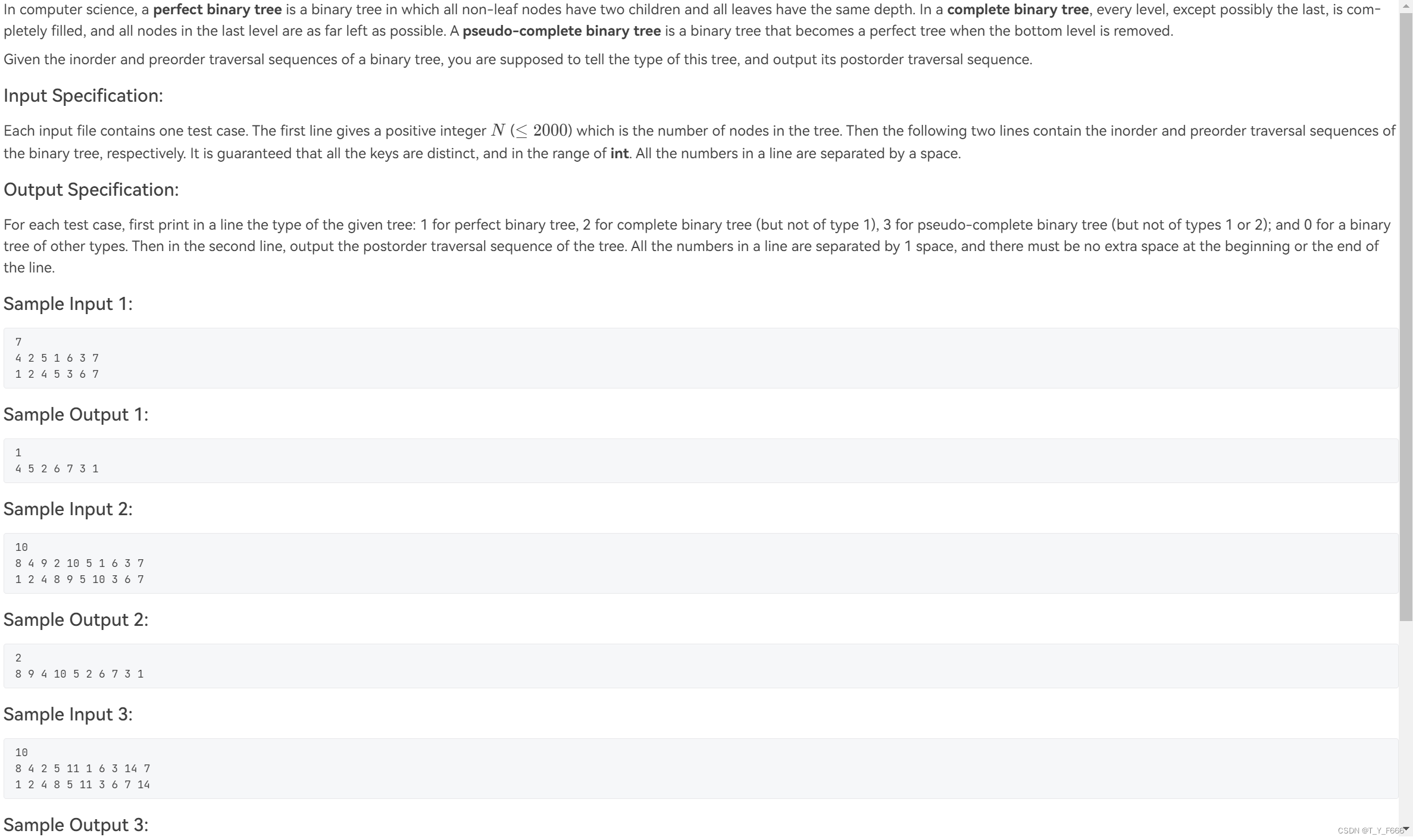
7-4 Pseudo-completeness

分数 30

原题

在这里插入图片描述

算法标签

树 dfs 模拟

思路

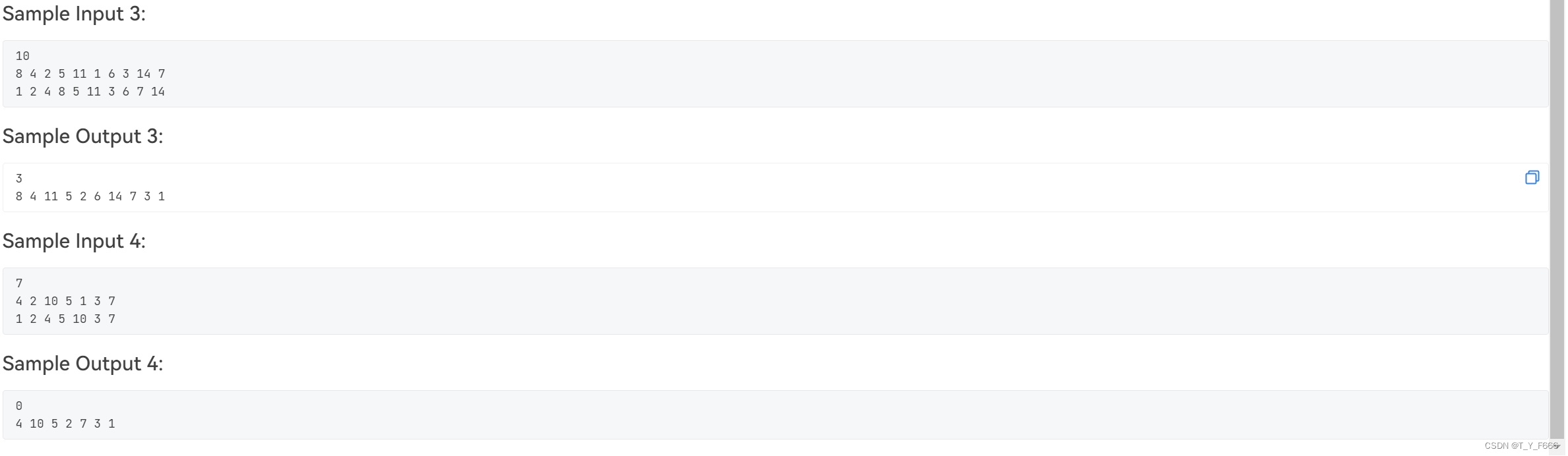
po[]存储后序遍历序列，d为层序遍历从左到右的序号（从0开始），f标记当前序号有无结点，mx为最大深度；
从前往后遍历第一个未被标记的节点序号：
①为n，且结点数量为2的n次方减1，则为perfect binary tree；
②为n，且结点数量不为2的n次方减1，则为complete binary tree；
③不为n，且在mx减1层的结点之后，则为pseudo-complete binary tree。

代码

#pragma GCC optimize(2)
#pragma GCC optimize(3)
#include<bits/stdc++.h>
#define int long long
#define xx first
#define yy second
#define ump unordered_map
#define us unordered_set
#define pb push_back
#define pq priority_queue
#define rep(i, a, b) for(int i=a;i<b;++i)
#define Rep(i, a, b) for(int i=a;i>=b;--i)
using namespace std;
const int N = 10005, inf=0x3f3f3f3f3f3f3f3f, mod=1e9+7;
const double Exp=1e-8;
int pre[N], in[N], po[N], f[N];
bool st[N];
int mx, p;
inline int rd(){
   int s=0,w=1;
   char ch=getchar();
   while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
   while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar();
   return s*w;
}
void put(int x) {
    if(x<0) putchar('-'),x=-x;
    if(x>=10) put(x/10);
    putchar(x%10^48);
}
void dfs(int u, int l, int r, int d, int le){
	if(l>r){
		return;
	}
	f[d]=true;
	mx=max(mx, le);
	int t=l;
	while(pre[u]!=in[t]){
		t++;
	}
	dfs(u+1, l, t-1, d*2+1, le+1);
	dfs(u+1+(t-l), t+1, r, d*2+2, le+1);
	po[p++]=pre[u];
}

signed main(){
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);
	int n=rd();
	rep(i, 1, n+1){
		in[i]=rd();
	}
	rep(i, 1, n+1){
		pre[i]=rd();
	}
	dfs(1, 1, n, 0, 1);
	rep(i, 0, n+1){
		if(!f[i]){
			if(i==n&&log2(n+1)==(int)log2(n+1)){
				puts("1");
			}else if(i==n){
				puts("2");
			}else if(i>=pow(2, mx-1)){
				puts("3");
			}else{
				puts("0");
			}
			break;
		}
	}
	printf("%lld", po[0]);
	rep(i, 1, n){
		printf(" %lld", po[i]);	
	}
	return 0;
}