卷积神经网络，Convolutinal Neural Network，CNN

在之前两章的由线性模型构成的神经网络都是全连接神经网络

一、CNN 基础

在之前全连接层处理二维图像的时候，直接将二维图像从 $N\times 1\times 28\times 28$ 直接转换成了 $N\times 784$，也就是将一个二维图像每一行数据直接拼接成了一行，这种做法，直接图像上可能相邻两个点的空间信息。

卷积神经网络概述：

1 个 patch：

单一输入通道卷积层的计算过程：

3 个输入通道卷积层的计算过程：

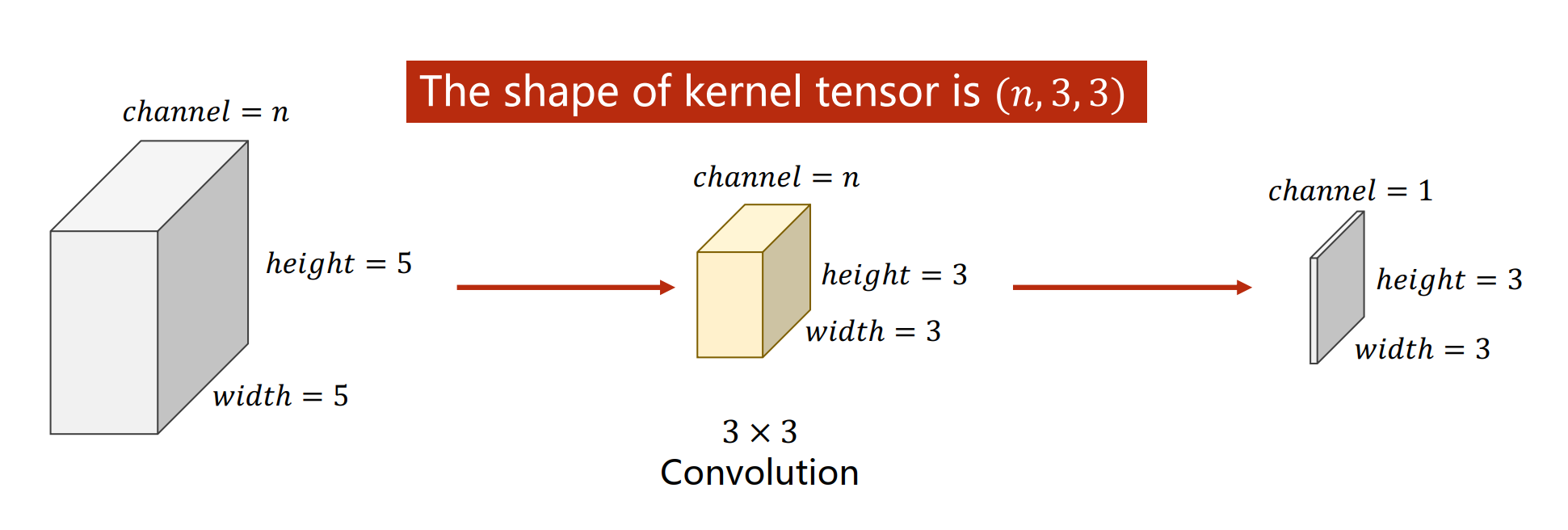
N 个输入通道卷积层的计算过程：

N 个输入通道 M 个输出通道卷积层的计算过程：

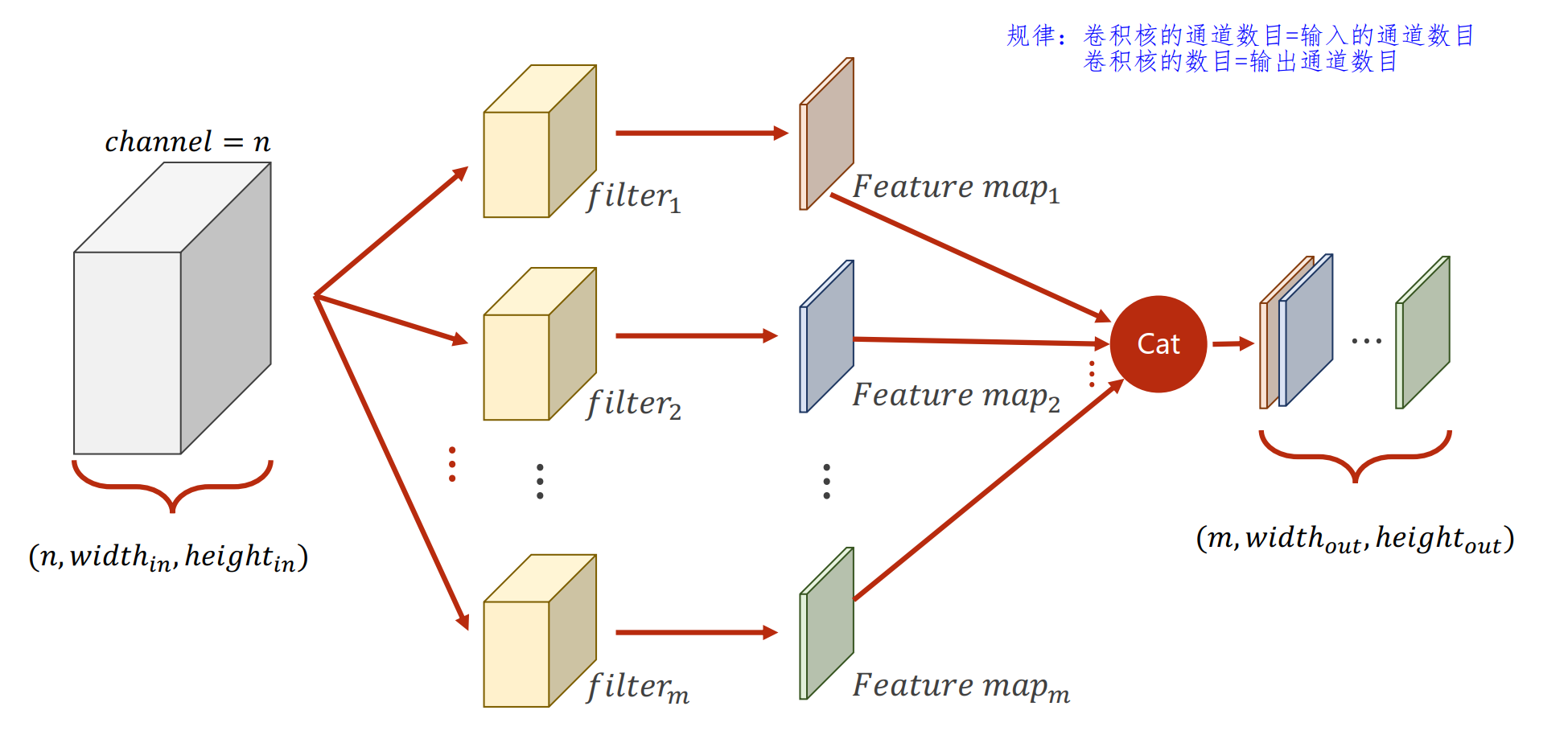
卷积核的大小：

使用 Pytorch 实现卷积层的一个例子：

import torch

in_channels, out_channels = 5, 10
width, height = 100, 100
kernel_size = 3
batch_size = 1

input = torch.randn(batch_size, in_channels, width, height)  # 正态分布随机采样，需要先指定batch-size，然后再指定通道数目、宽度、高度
conv_layer = torch.nn.Conv2d(in_channels, out_channels, kernel_size=kernel_size)
output = conv_layer(input)

print(input.shape)
print(output.shape)
print(conv_layer.weight.shape)

# 输出：
# torch.Size([1, 5, 100, 100])
# torch.Size([1, 10, 98, 98])
# torch.Size([10, 5, 3, 3])

卷积层重要概念：padding，这里 padding=1。

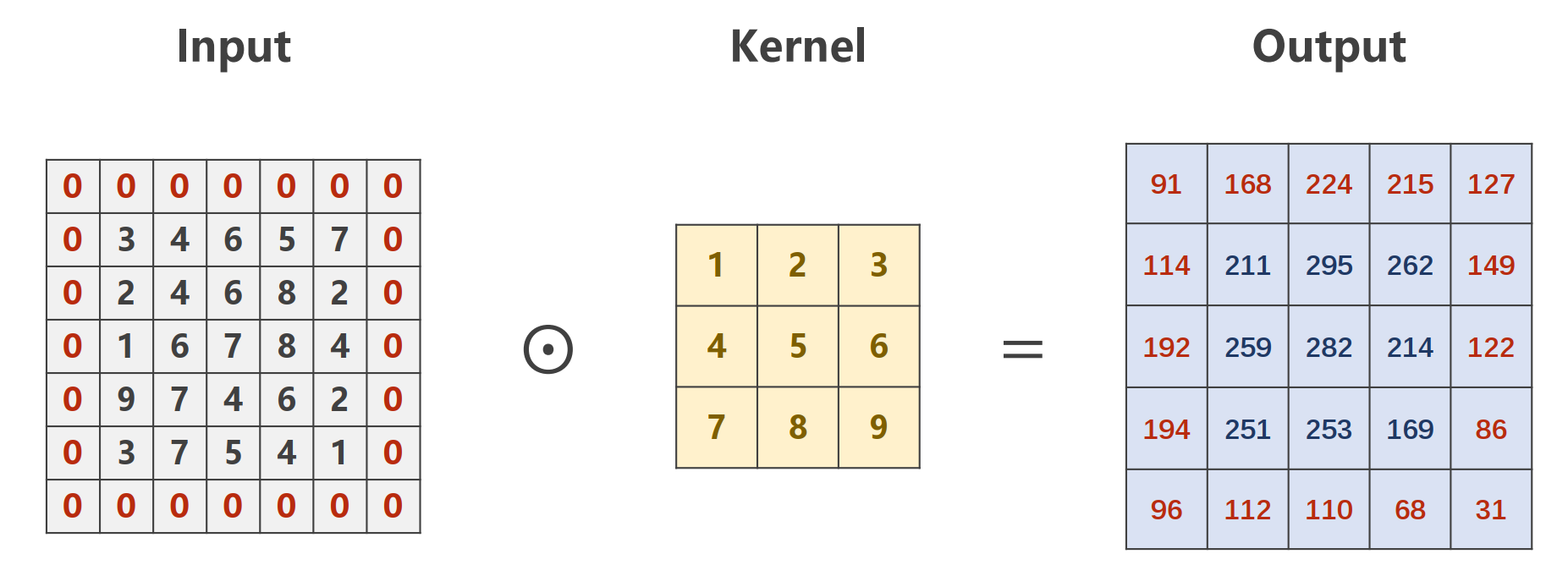
假设卷积核的高和宽均为 $x$，在每一次通过卷积层的时候，如果 padding=0，那么输入矩阵的高和宽在输出卷积层的时候会减少 $2\times \lfloor \frac{x}{2}\rfloor$ 的长度。

卷积层重要概念：stride（步长），这里 stride=2。要注意，图中红色矩形往右移动或者往下移动的步长都是 2！

padding 与 stride 在代码中的设置：

conv_layer = torch.nn.Conv2d(in_channels, out_channels, kernel_size=kernel_size, padding=1, stride=2,
                             bias=False)  # bias为True会对最终结果产生一个偏置值

下采样（Subsampling）常用方法：最大池化层（Max Pooling Layer），默认 stride=2。注意最大池化层与通道数目无关，它会在每一个通道上分别进行池化作用。

Pytorch 代码简单实现：

import torch

input = [3, 4, 6, 5,
         2, 4, 6, 8,
         1, 6, 7, 8,
         9, 7, 4, 6]

input = torch.Tensor(input).view(1, 1, 4, 4)
maxpooling_layer = torch.nn.MaxPool2d(kernel_size=2)  # 默认stride=2
output = maxpooling_layer(input)
print(output)

一个简单卷积神经网络样例：

代码实现（依然使用 MNIST 数据集）：

import torch
from torchvision import transforms
from torchvision import datasets
from torch.utils.data import DataLoader
import torch.nn.functional as F
import torch.optim as optim

batch_size = 64
transform = transforms.Compose(
    [transforms.ToTensor(), transforms.Normalize((0.1307,), (0.3081,))])  # 归一化并将图像从单通道转换为多通道，即28x28转换为1x28x28

train_dataset = datasets.MNIST(root='./Data/mnist/', train=True, download=True, transform=transform)
train_loader = DataLoader(train_dataset, shuffle=True, batch_size=batch_size)

test_dataset = datasets.MNIST(root='./Data/mnist', train=False, download=True, transform=transform)
test_loader = DataLoader(test_dataset, shuffle=False, batch_size=batch_size)


class Net(torch.nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.conv1 = torch.nn.Conv2d(1, 10, kernel_size=5)
        self.conv2 = torch.nn.Conv2d(10, 20, kernel_size=5)
        self.pooling = torch.nn.MaxPool2d(2)
        self.fc = torch.nn.Linear(320, 10)  # 320 = 20 * 4 * 4

    def forward(self, x):
        batch_size = x.size(0)
        x = self.pooling(F.relu(self.conv1(x)))
        x = self.pooling(F.relu(self.conv2(x)))
        x = x.view(batch_size, -1)
        x = self.fc(x)
        return x


model = Net()
device = torch.device("cuda:0" if torch.cuda.is_available() else "cup")
model.to(device)  # 将模型放到GPU上

criterion = torch.nn.CrossEntropyLoss()
optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.5)  # 添加了动量


def train(epoch):  # 将每一轮训练封装成一个函数
    running_loss = 0.0
    for batch_idx, data in enumerate(train_loader, 0):
        inputs, target = data
        inputs, target = inputs.to(device), target.to(device)  # 将数据放到GPU上
        optimizer.zero_grad()

        outputs = model(inputs)
        loss = criterion(outputs, target)
        loss.backward()
        optimizer.step()

        running_loss += loss.item()
        if batch_idx % 300 == 299:
            print('[%d, %5d] loss: %.3f' % (epoch + 1, batch_idx + 1, running_loss / 300))
            running_loss = 0.0


def test():
    correct = 0  # 预测正确的数目
    total = 0  # 总共的数目
    with torch.no_grad():  # with范围内的代码不计算梯度
        for data in test_loader:
            images, labels = data
            images, labels = images.to(device), labels.to(device)  # 将数据放到GPU上
            outputs = model(images)
            _, predicted = torch.max(outputs.data, dim=1)  # 返回(最大值, 最大值下标)
            total += labels.size(0)  # label是一个矩阵
            correct += (predicted == labels).sum().item()
    print('Accuracy on test set: %d %%' % (100 * correct / total))


if __name__ == '__main__':
    for epoch in range(10):
        train(epoch)
        test()

二、CNN 进阶

减少代码冗余的方法：

• 面向过程的语言：使用函数
• 面向对象的语言：使用类

比较复杂的 CNN 模型：GoogleNet

Inception Module（初始模型）：

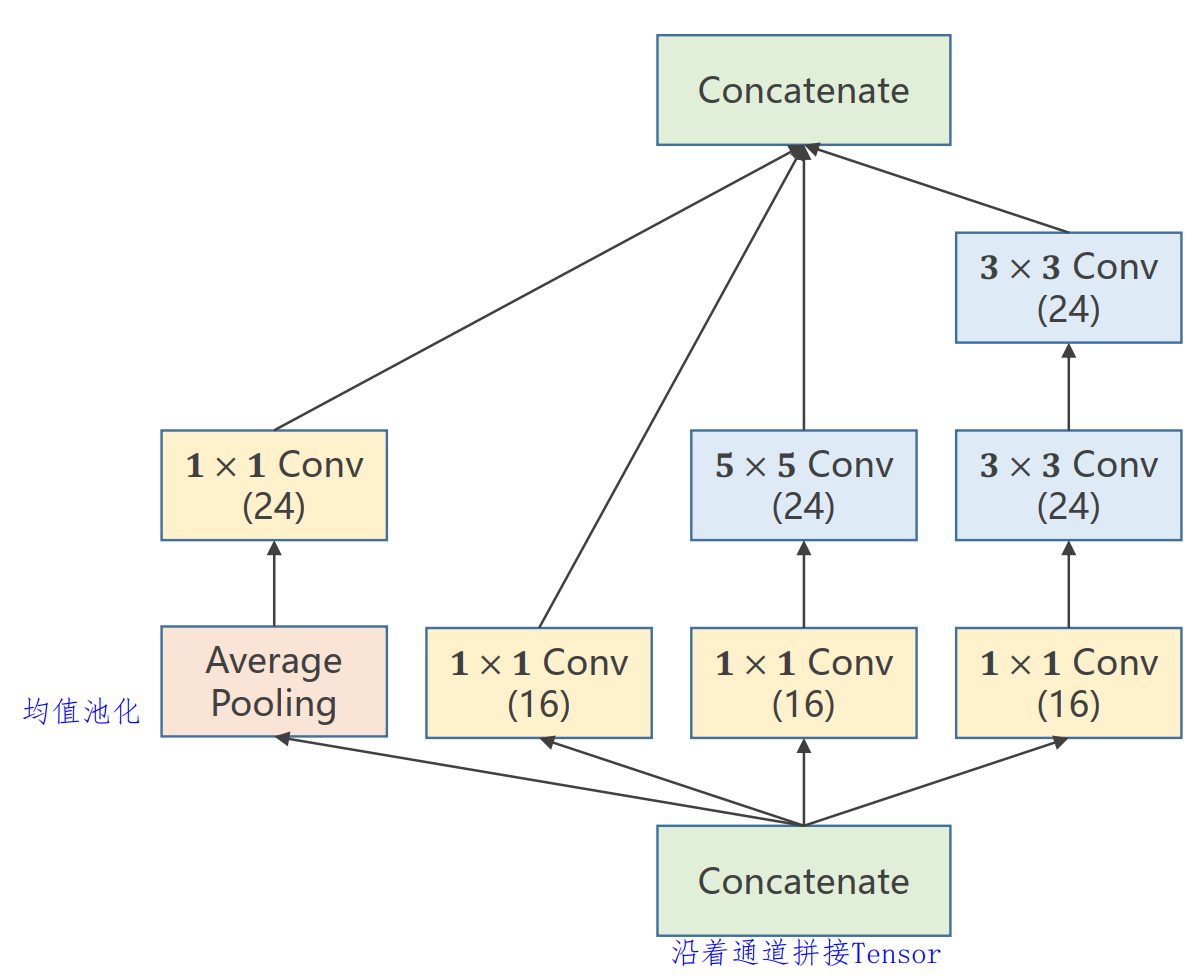
• Inception Module 如此设计的目的：在神经网络中，对于卷积核的大小（超参数）很难以确定，这里就将所有的卷积核大小全部都操作一遍，最后将其结果综合起来。如果其中某一个方案比较好，其所占比重就会比较大，上图中就存在四种方案。
• 最后在 Concatenate 的时候，四种方案的输出维度（batch-size，通道，w，h）中只有 通道 数目不同，其余都相同。

1x1 卷积层（Network in Network）：

1x1 卷积层的作用：1x1 卷积的作用：改变通道数目，减少计算量。它的直接效果是信息融合，即对同一个通道上所有像素点的信息进行了融合。

使用 1x1 卷积层与不使用 1x1 卷积层的效果对比：

模型实现图：

实现代码：

import torch
from torchvision import transforms
from torchvision import datasets
from torch.utils.data import DataLoader
import torch.nn.functional as F
import torch.optim as optim

batch_size = 64
transform = transforms.Compose(
    [transforms.ToTensor(), transforms.Normalize((0.1307,), (0.3081,))])  # 归一化并将图像从单通道转换为多通道，即28x28转换为1x28x28

train_dataset = datasets.MNIST(root='./Data/mnist/', train=True, download=True, transform=transform)
train_loader = DataLoader(train_dataset, shuffle=True, batch_size=batch_size)

test_dataset = datasets.MNIST(root='./Data/mnist', train=False, download=True, transform=transform)
test_loader = DataLoader(test_dataset, shuffle=False, batch_size=batch_size)


class InceptionA(torch.nn.Module):
    def __init__(self, in_channels):
        super(InceptionA, self).__init__()
        self.branch1x1 = torch.nn.Conv2d(in_channels, 16, kernel_size=1)

        self.branch5x5_1 = torch.nn.Conv2d(in_channels, 16, kernel_size=1)
        self.branch5x5_2 = torch.nn.Conv2d(16, 24, kernel_size=5, padding=2)  # padding=2保证图像w、h不变

        self.branch3x3_1 = torch.nn.Conv2d(in_channels, 16, kernel_size=1)
        self.branch3x3_2 = torch.nn.Conv2d(16, 24, kernel_size=3, padding=1)
        self.branch3x3_3 = torch.nn.Conv2d(24, 24, kernel_size=3, padding=1)

        self.branch_pool = torch.nn.Conv2d(in_channels, 24, kernel_size=1)

    def forward(self, x):
        branch1x1 = self.branch1x1(x)

        branch5x5 = self.branch5x5_1(x)
        branch5x5 = self.branch5x5_2(branch5x5)

        branch3x3 = self.branch3x3_1(x)
        branch3x3 = self.branch3x3_2(branch3x3)
        branch3x3 = self.branch3x3_3(branch3x3)

        branch_pool = F.avg_pool2d(x, kernel_size=3, stride=1, padding=1)  # stride=padding=1，保证图像w、h不变
        branch_pool = self.branch_pool(branch_pool)

        outpus = [branch1x1, branch5x5, branch3x3, branch_pool]

        return torch.cat(outpus, dim=1)


class Net(torch.nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.conv1 = torch.nn.Conv2d(1, 10, kernel_size=5)
        self.conv2 = torch.nn.Conv2d(88, 20, kernel_size=5)  # 这里的 88 = 24 + 24 + 24 + 16

        self.incep1 = InceptionA(in_channels=10)
        self.incep2 = InceptionA(in_channels=20)

        self.mp = torch.nn.MaxPool2d(2)
        self.fc = torch.nn.Linear(1408, 10)

    def forward(self, x):
        in_size = x.size(0)
        x = F.relu(self.mp(self.conv1(x)))
        x = self.incep1(x)
        x = F.relu(self.mp(self.conv2(x)))
        x = self.incep2(x)
        x = x.view(in_size, -1)
        x = self.fc(x)
        return x


model = Net()
device = torch.device("cuda:0" if torch.cuda.is_available() else "cup")
model.to(device)  # 将模型放到GPU上

criterion = torch.nn.CrossEntropyLoss()
optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.5)  # 添加了动量


def train(epoch):  # 将每一轮训练封装成一个函数
    running_loss = 0.0
    for batch_idx, data in enumerate(train_loader, 0):
        inputs, target = data
        inputs, target = inputs.to(device), target.to(device)  # 将数据放到GPU上
        optimizer.zero_grad()

        outputs = model(inputs)
        loss = criterion(outputs, target)
        loss.backward()
        optimizer.step()

        running_loss += loss.item()
        if batch_idx % 300 == 299:
            print('[%d, %5d] loss: %.3f' % (epoch + 1, batch_idx + 1, running_loss / 300))
            running_loss = 0.0


def test():
    correct = 0  # 预测正确的数目
    total = 0  # 总共的数目
    with torch.no_grad():  # with范围内的代码不计算梯度
        for data in test_loader:
            images, labels = data
            images, labels = images.to(device), labels.to(device)  # 将数据放到GPU上
            outputs = model(images)
            _, predicted = torch.max(outputs.data, dim=1)  # 返回(最大值, 最大值下标)
            total += labels.size(0)  # label是一个矩阵
            correct += (predicted == labels).sum().item()
    print('Accuracy on test set: %d %%' % (100 * correct / total))


if __name__ == '__main__':
    for epoch in range(10):
        train(epoch)
        test()

添加 Inception Module 后计算精度从 97% 提高到了 98%。

添加更深层次的模型：Plain Nets

由上图可以知道，针对数据集 CIFAR-10 而言，在 20 层模型的训练损失要比 50 层模型训练的损失低很多。这可能是由于过拟合导致的结果，也有可能是梯度消失造成的。

之所以会发生梯度消失，是因为在反向传播的过程中，如果损失函数 $L$ 对某一个变量 $\omega$ 的梯度 $$\frac{\partial L}{\partial \omega }<1$$那么在进行更新权重的时候，因为是链式法则（乘法），就会导致下式 $$\omega =\omega -\alpha \frac{\partial L}{\partial \omega }$$ 变成 $$\omega =\omega -\alpha \cdot 0=\omega$$其效果就是梯度不更新了，求出来的损失恒定。

为了解决这个问题，提出了 Deep Residual Learning 模型（残差模型）：

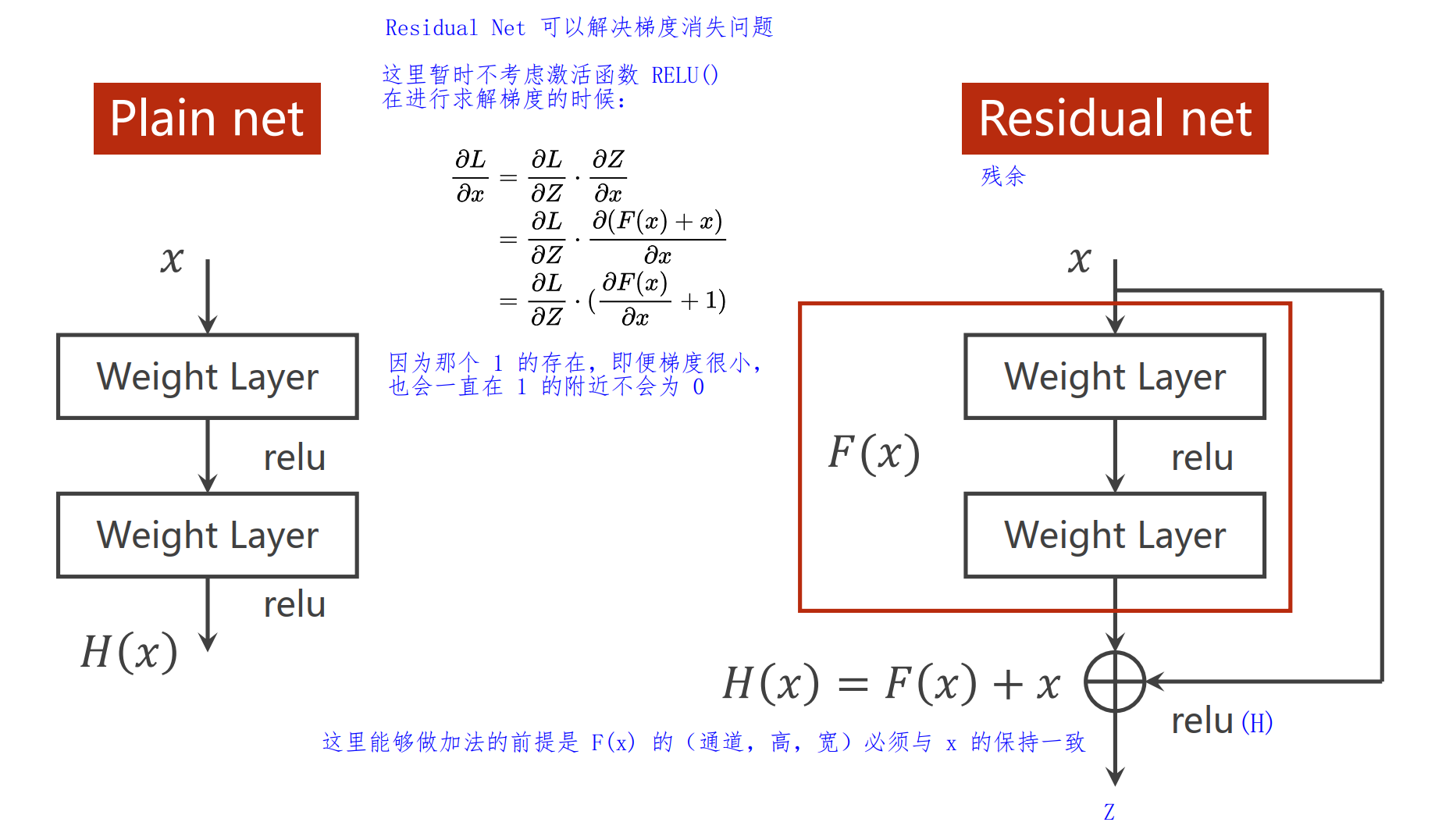
如图中所示，该模型能够解决梯度消失的办法就是在激活函数之前加上了最初输入模型的 $x$，后续反向传播过程中会有$$\frac{\partial L}{\partial \omega }>1$$即便梯度非常小，它也会在 $\ge 1$ 的附近，永远不会为 $0$。

Deep Resdual Learning 模型代码实现：

import torch
from torchvision import transforms
from torchvision import datasets
from torch.utils.data import DataLoader
import torch.nn.functional as F
import torch.optim as optim

batch_size = 64
transform = transforms.Compose(
    [transforms.ToTensor(), transforms.Normalize((0.1307,), (0.3081,))])  # 归一化并将图像从单通道转换为多通道，即28x28转换为1x28x28

train_dataset = datasets.MNIST(root='./Data/mnist/', train=True, download=True, transform=transform)
train_loader = DataLoader(train_dataset, shuffle=True, batch_size=batch_size)

test_dataset = datasets.MNIST(root='./Data/mnist', train=False, download=True, transform=transform)
test_loader = DataLoader(test_dataset, shuffle=False, batch_size=batch_size)


class ResidualBlock(torch.nn.Module):
    def __init__(self, channels):
        super(ResidualBlock, self).__init__()
        self.channels = channels  # 该层必须要保证输入输出Tensor维度相同
        self.conv1 = torch.nn.Conv2d(channels, channels, kernel_size=3, padding=1)
        self.conv2 = torch.nn.Conv2d(channels, channels, kernel_size=3, padding=1)

    def forward(self, x):
        y = F.relu(self.conv1(x))
        y = self.conv2(y)
        return F.relu(x + y)  # 先相加，后激活


class Net(torch.nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.conv1 = torch.nn.Conv2d(1, 16, kernel_size=5)
        self.conv2 = torch.nn.Conv2d(16, 32, kernel_size=5)
        self.mp = torch.nn.MaxPool2d(2)

        self.rblock1 = ResidualBlock(16)
        self.rblock2 = ResidualBlock(32)

        self.fc = torch.nn.Linear(512, 10)

    def forward(self, x):
        in_size = x.size(0)
        x = self.mp(F.relu(self.conv1(x)))
        x = self.rblock1(x)
        x = self.mp(F.relu(self.conv2(x)))
        x = self.rblock2(x)
        x = x.view(in_size, -1)
        x = self.fc(x)
        return x


model = Net()
device = torch.device("cuda:0" if torch.cuda.is_available() else "cup")
model.to(device)  # 将模型放到GPU上

criterion = torch.nn.CrossEntropyLoss()
optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.5)  # 添加了动量


def train(epoch):  # 将每一轮训练封装成一个函数
    running_loss = 0.0
    for batch_idx, data in enumerate(train_loader, 0):
        inputs, target = data
        inputs, target = inputs.to(device), target.to(device)  # 将数据放到GPU上
        optimizer.zero_grad()

        outputs = model(inputs)
        loss = criterion(outputs, target)
        loss.backward()
        optimizer.step()

        running_loss += loss.item()
        if batch_idx % 300 == 299:
            print('[%d, %5d] loss: %.3f' % (epoch + 1, batch_idx + 1, running_loss / 300))
            running_loss = 0.0


def test():
    correct = 0  # 预测正确的数目
    total = 0  # 总共的数目
    with torch.no_grad():  # with范围内的代码不计算梯度
        for data in test_loader:
            images, labels = data
            images, labels = images.to(device), labels.to(device)  # 将数据放到GPU上
            outputs = model(images)
            _, predicted = torch.max(outputs.data, dim=1)  # 返回(最大值, 最大值下标)
            total += labels.size(0)  # label是一个矩阵
            correct += (predicted == labels).sum().item()
    print('Accuracy on test set: %d %%' % (100 * correct / total))


if __name__ == '__main__':
    for epoch in range(10):
        train(epoch)
        test()