计算机视觉的应用5-利用PCA降维方法实现简易人脸识别模型

news2024/10/7 8:27:22

大家好，我是微学AI，今天给大家介绍一下计算机视觉的应用5-利用PCA降维方法实现简易人脸识别模型，本文将介绍如何使用主成分分析（PCA）实现简易的人脸识别模型。首先，我们将简要介绍PCA的原理及其在人脸识别中的应用。接着，我们将通过实例演示如何使用Python实现PCA降维，并给出完整的代码示例。

文章目录

一、引言
二、PCA原理
三、 PCA在人脸识别中的应用
四、简易人脸识别模型实现
- 4.1 数据预处理
- 4.2 实现PCA降维
- 4.3 计算欧氏距离进行人脸识别
- 4.4 代码实现
5. 总结

一、引言

主成分分析（PCA）是一种广泛应用于数据降维、压缩和可视化的技术。它通过线性变换将原始数据转换为一组新的变量（即主成分），其中每个新变量都是原始变量的线性组合，且它们按照重要性进行排序，使得第一个主成分尽量保留原始数据中的信息，而后续主成分则依次捕获剩余的信息。因此，PCA可以将原始数据压缩成更少的维度，从而更容易进行数据分析和可视化。具体来说，假设有m个n维数据样本，将它们表示为一个m x n的矩阵X。在人脸识别领域，PCA可以用于提取人脸图像的主要特征，从而降低数据维度，减少计算量，同时保持较高的识别率。

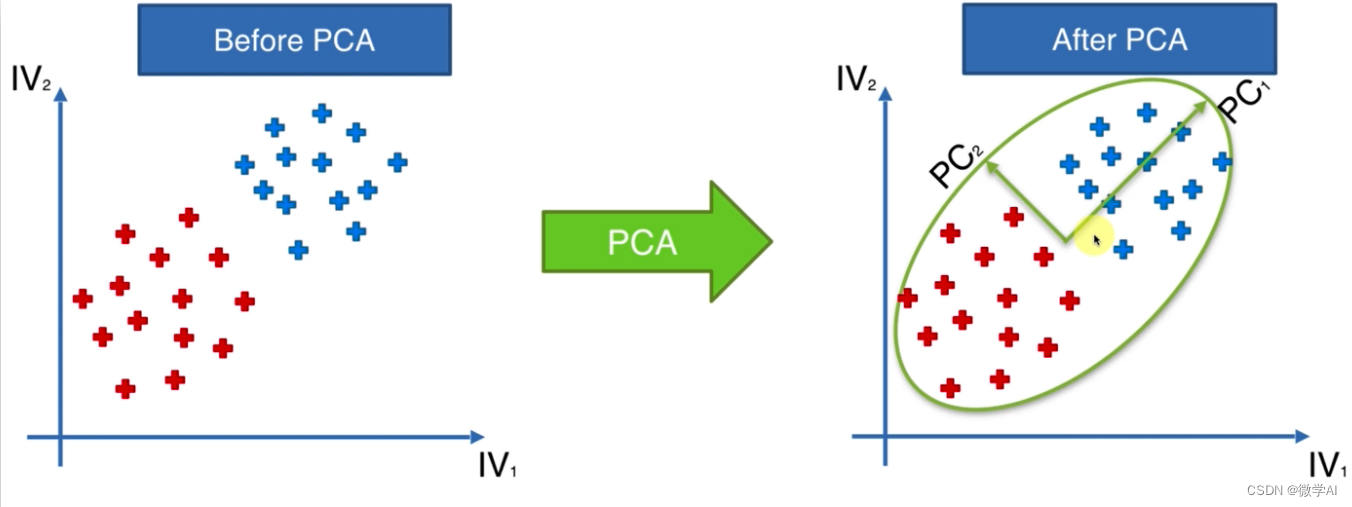
二、PCA原理

PCA的目标是将高维数据投影到低维空间，同时保持数据的主要特征。具体步骤如下：

1.计算数据的均值向量和协方差矩阵；

2.计算协方差矩阵的特征值和特征向量；

3.按降序排列特征值，选择前k个最大的特征值对应的特征向量组成投影矩阵（k为降维后的维度）；

4.将数据投影到投影矩阵上，得到降维后的数据。

三、PCA在人脸识别中的应用

在人脸识别问题中，我们可以将图像数据看作是高维空间中的点。通过PCA降维，我们可以将图像投影到低维空间，同时保留主要的特征信息。然后，我们可以通过计算欧氏距离等方法来度量图像间的相似性，从而实现人脸识别。

四、简易人脸识别模型实现

4.1 数据预处理

在开始实现PCA降维之前，我们需要对数据进行预处理。具体步骤如下：

1.读取人脸图像数据；

2.将图像转换为灰度图像；

3.将灰度图像转换为一维向量；

4.将所有图像向量堆叠为一个矩阵。

4.2 实现PCA降维

在实现PCA降维时，我们可以利用Python中的NumPy库提供的函数来完成前述PCA原理中的计算步骤。

4.3 计算欧氏距离进行人脸识别

在完成PCA降维后，我们可以计算测试图像与训练图像在降维空间中的欧氏距离，然后选择距离最近的图像作为识别结果。

4.4 代码实现

以下是使用PCA实现简易人脸识别模型的完整代码：

import numpy as np
import cv2
import os

def load_images(path):
    images = []
    labels = []
    for subdir, dirs, files in os.walk(path):
        for file in files:
            img_path = os.path.join(subdir, file)
            img = cv2.imread(img_path, cv2.IMREAD_GRAYSCALE)
            img = cv2.resize(img, (248, 248))
            img_vector = img.flatten()
            images.append(img_vector)
            labels.append(subdir.split("/")[-1])
    return np.array(images), np.array(labels)

def pca(X, k):
    #print(X.shape)
    mean = np.mean(X, axis=0)
    X_centered = X - mean
    cov_matrix = np.cov(X_centered.T)
    # 使用 atleast_2d 函数将 cov_matrix 转换为至少有两个维度的数组
    cov_matrix = np.atleast_2d(cov_matrix)

    eig_vals, eig_vecs = np.linalg.eig(cov_matrix)
    sorted_indices = np.argsort(eig_vals)[::-1]
    top_k_eig_vecs = eig_vecs[:, sorted_indices[:k]]
    X_centered = X_centered.reshape(-1, 1)
    print(X_centered.shape)
    #top_k_eig_vecs = top_k_eig_vecs.T
    X_pca = X_centered.dot(top_k_eig_vecs)
    return X_pca, top_k_eig_vecs, mean

def euclidean_distance(a, b):
    return np.sqrt(np.sum((a - b) ** 2))

def face_recognition(test_image, train_images, train_labels, eig_vecs, mean):
    test_image_centered = test_image - mean
    test_image_centered =test_image_centered.reshape(-1, 1)

    test_image_pca = test_image_centered.dot(eig_vecs)
    print(test_image_pca.shape)
    min_distance = float("inf")
    best_match = None
    train_images =[train_images]
    for i, train_image_pca in enumerate(train_images):
        print(test_image_pca.shape)
        distance = euclidean_distance(test_image_pca, train_image_pca)
        if distance < min_distance:
            min_distance = distance
            best_match = train_labels[i]
    return best_match

if __name__ == "__main__":
    train_images_path = "图片文件夹"
    test_image_path = "1.png"

    # Load and preprocess images
    train_images, train_labels = load_images(train_images_path)
    print(train_images, train_labels)
    test_image = cv2.imread(test_image_path, cv2.IMREAD_GRAYSCALE)
    test_image = cv2.resize(test_image, (248, 248))
    test_image_vector = test_image.flatten()
    #train_images = np.stack(train_images, axis=1)
    # Perform PCA on training images
    k = 50
    train_images_pca, eig_vecs, mean = pca(train_images[0], k)

    # Perform face recognition
    result = face_recognition(test_image_vector, train_images_pca, train_labels, eig_vecs, mean)
    print("测试的图片类别是:", result)

请注意替换"图片文件夹"和“1.png”为实际的训练图像和测试图像路径。