1. 解决了什么问题？

DETR 去除了目标检测算法中的人为设计，取得了不错的表现。但是其收敛速度很慢，对低分辨率特征识别效果差：

• 模型初始化时，注意力模块给特征图上所有的像素点分配的权重是均匀的，就需要较长的训练 epochs 使注意力权重学习关注到稀疏的、有意义的像素位置。
• Transformer encoder 中的注意力权重的计算量关于像素的个数是 quadratic，因此计算量和内存占用就非常高。
• 缺少多尺度特征来检测小目标。

2. 提出了什么方法？

Deformable DETR 将 deformable conv 的稀疏空间采样和 transformer 的关系建模能力结合，缓解了收敛慢和高复杂度的问题，提出了 deformable attention 模块，只关注于特征图上每个像素少量的采样位置。

2.1 Multi-head Attention

给定一个 query element 以及一个 key elements 的集合，multi-head attention 模块根据注意力权重聚合 key 对应的 values，该注意力权重表示 query-key pairs 之间的匹配程度。为了让模型关注于不同表征子空间和位置的内容，我们将不同的 attention heads 的输出用可学习的权重线性聚合起来。$q\in {\Omega }_q$是 query，其对应的表征是$z_q\in {\mathbb{R}}^C$。$k\in {\Omega }_k$是 key，对应表征是$x_k\in {\mathbb{R}}^C$，$C$是特征维度。Multi-head attention 特征计算过程如下：

$$\text{MultiHeadAttn}(z_q,x)=\sum _{m=1}^M{W}_m\left[\sum _{k\in {\Omega }_k}{A}_{mqk}\cdot W_m^{\prime }{x}_k\right]$$

其中$m$是 attention head 索引，$W_m^{\prime }\in {\mathbb{R}}^{C_v\times C},W_m\in {\mathbb{R}}^{C\times C_v}$是可学习权重（$C_v=C/M$）。注意力权重 A m q k ∝ exp ⁡ { z q T U m T V m x k C v } A_{mqk}\propto \exp\lbrace \frac{z_q^T U_m^T V_m x_k}{\sqrt{C_v}} \rbrace Amqk​∝exp{Cv​ ​zqT​UmT​Vm​xk​​}，并且${\sum }_{k\in {\Omega }_k}{A}_{mqk}=1$，其中$U_m,V_m\in {\mathbb{R}}^{C_v\times C}$是 query 和 key 的映射矩阵，也是可学习权重。为了区分不同空间位置，$z_q$和$x_k$会加上 positional encodings。在图像里面，query 和 key 元素都是像素点，因此 MultiHeadAttn 的复杂度是$\mathcal{O}(N_q{C}^2+N_k{C}^2+N_q{N}_{k}C),N_q=N_k\gg C$，复杂度由第三项决定，因此 multi-head attn 的复杂度与特征图大小呈 quadratic。

2.2 Deformable Attention Module

在图像特征上使用 transformer attention，它会查看所有可能的空间位置。于是，作者提出了 deformable attention，它只会关注于 reference point 附近的 key sampling points，不管特征图有多大。这样，就缓解了收敛速度慢和空间分辨率的问题。
给定特征图$x\in {\mathbb{R}}^{C\times H\times W}$，$q$是 query 的索引，对应的特征是 $z_q$，$p_q$是 2D reference point，deformable attention 特征计算过程如下：
$$\text{DeformAttn}(z_q,p_q,x)=\sum _{m=1}^M{W}_m\left[\sum _{k=1}^K{A}_{mqk}\cdot W_m^{\prime }\cdot x(p_q+\Delta p_{mqk})\right]$$

$m$是注意力 head 的索引，$k$是采样 keys 的索引，$K$是所有采样点的个数（$K\ll HW$）。$\Delta p_{mqk}$和 $A_{mqk}$分别表示第$m$个注意力 head 里面第$k$个采样点的偏移量和注意力权重。$A_{mqk}\in [0,1],{\sum }_{k=1}^K{A}_{mqk}=1,\Delta p_{mqk}\in {\mathbb{R}}^2$。通过双线性插值计算出$x(p_q+\Delta p_{mqk})$，对$z_q$做 linear projection 得到$\Delta p_{mqk},A_{mqk}$。将$z_q$输入进一个$3MK$通道的 linear projection ，前$2MK$个通道编码了采样点偏移量$\Delta p_{mqk}$，后$MK$个通道输入进 softmax 得到注意力权重$A_{mqk}$。

2.2.1 计算复杂度

$N_q$是 query 个数，$MK$相对较小，deformable attention 模块的复杂度就是 $\mathcal{O}(2N_q{C}^2+\min (HW{C}^2,N_{q}K{C}^2))$，过程如下：

• 计算采样坐标偏移量$\Delta p_{mqk}$和注意力权重 $A_{mqk}$的复杂度是$\mathcal{O}(N_{q}C\cdot 3MK)$。
• 在 decoder 中，有了坐标偏移量和注意力权重，DeformAttn 的复杂度就是$\mathcal{O}(N_q{C}^2+N_{q}K{C}^2+5N_{q}KC)$，其中$5N_{q}KC$是因为注意力的双线性插值和加权和操作。
• 在 encoder 中，$N_q=HW$，我们可以在采样前计算$W_m^{\prime }x$，DeformAttn 的复杂度就是$\mathcal{O}(N_q{C}^2+HW{C}^2+5N_{q}KC)$。
• 总的复杂度就是$\mathcal{O}(N_q{C}^2+\min (N_{q}K{C}^2,HW{C}^2)+5N_{q}KC+3N_{q}CMK)$，在实验中$M=8,K\le 4,C=256$，因此$5K+3MK<C$，因此复杂度为$\mathcal{O}(2N_q{C}^2+\min (HW{C}^2,N_{q}K{C}^2))$。

2.3 多尺度 Deformable Attention 模块

{ x l } l = 1 L \lbrace x^l \rbrace^L_{l=1} {xl}l=1L​是多尺度特征图，其中$x^l\in {\mathbb{R}}^{C\times H_l\times W_l}$。$\hat{p}_q\in \left[ 0,1\right]^2 $是每个 query $q$的 reference point 归一化后的坐标，多尺度 deformable attention 模块计算过程为：

MSDeformAttn ( z q , p ^ q , { x l } l = 1 L ) = ∑ m = 1 M W m [ ∑ l = 1 L ∑ k = 1 K A m l q k ⋅ W m ′ ⋅ x l ( ϕ l ( p ^ q ) + Δ p m l q k ) ] \text{MSDeformAttn}(z_q,\hat{p}_q,\lbrace x^l \rbrace_{l=1}^L)=\sum_{m=1}^M W_m \left[ \sum_{l=1}^L \sum_{k=1}^K A_{mlqk} \cdot W'_m \cdot x^l (\phi_l(\hat{p}_q) + \Delta p_{mlqk}) \right] MSDeformAttn(zq​,p^​q​,{xl}l=1L​)=m=1∑M​Wm​[l=1∑L​k=1∑K​Amlqk​⋅Wm′​⋅xl(ϕl​(p^​q​)+Δpmlqk​)]

其中$m$是 attention head 的索引，$l$是输入特征层级的索引，$k$是采样点的索引。$\Delta p_{mlqk}$和 $A_{mlqk}$表示第 $l$个特征层级、第$m$个注意力 head 上第 $k$个采样点的采样位置偏移量和注意力权重，${\sum }_{l=1}^L{\sum }_{k=1}^K{A}_{mlqk}=1$。函数${\varphi }_l({\hat{p}}_q)$将归一化的坐标${\hat{p}}_q$重新缩放到第$l$层级的特征图上。

2.4 Deformable Transformer Encoder

Encoder 的输入和输出是分辨率相同的多尺度特征图。从 ResNet 中提取$C_3$到$C_5$阶段的输出特征图 { x l } l = 1 L − 1 ， ( L = 4 ) \lbrace x^l \rbrace_{l=1}^{L-1}，(L=4) {xl}l=1L−1​，(L=4)。其中$C_l$的分辨率要比输入图片小$2^l$。最低的分辨率是$C_6$，通过对$C_5$输出的特征图使用$3\times 3$且步长为 2 的卷积操作得到。所有的特征图通道数都是 256。
多尺度特征图的输出的分辨率与输入相同。Key 和 query 元素都是多尺度特征图上的像素点。对于 query 像素点，reference point 就是其本身。为了鉴别 query 像素所在的特征层级，作者在特征表征中加入了一个尺度层级 embedding，即 $e_l$。尺度层级 embedding { e l } l = 1 L \lbrace e_l \rbrace_{l=1}^L {el​}l=1L​随机初始化，与网络协同训练。

2.5 Deformable Transformer Decoder

Decoder 包括 cross attention 和 self attention。这两种 attention 模块的 query 元素都是 object queries。在 cross attention 中，object queries 从特征图上提取特征，key 元素来自于 encoder 输出的特征图。在 self attention 中，object queries 互相交流，key 元素就是 object queries。作者只将 cross attention 替换为了 multi-scale deformable attention，而保留了 self attention。对于每个 object query，使用 linear projection 以及一个 sigmoid 函数，预测一个reference point ${\hat{p}}_q$的 2D 归一化坐标。然后，检测 head 关于这个reference point 预测边框的坐标，降低优化难度。这个reference point 就可以看作为边框中心点的 initial guess。

2.6 实验

在 MS COCO 2017 数据集进行的实验。在主干网络中使用了 ImageNet 上预训练的 ResNet-50 权重，没有用 FPN 提取多尺度特征图。在 deformable attention 中， $M=8,K=4$。Deformable transformer encoder 中不同特征层级的参数共享权重。Focal Loss 中边框分类损失的权重设为 2。Object queries 个数设为了 300。所有的模型训练了 50 个 epochs，学习率在第 40 个 epoch 时乘以 0.1 衰减。模型训练采用了 Adam 优化器，初始学习率为 $2\times 10^{-4},{\beta }_1=0.9,{\beta }_2=0.999$，weight decay 为 $10^{-4}$。用于预测 object query reference point 和采样偏移量的 linear projection，它的学习率会乘以系数 0.1。

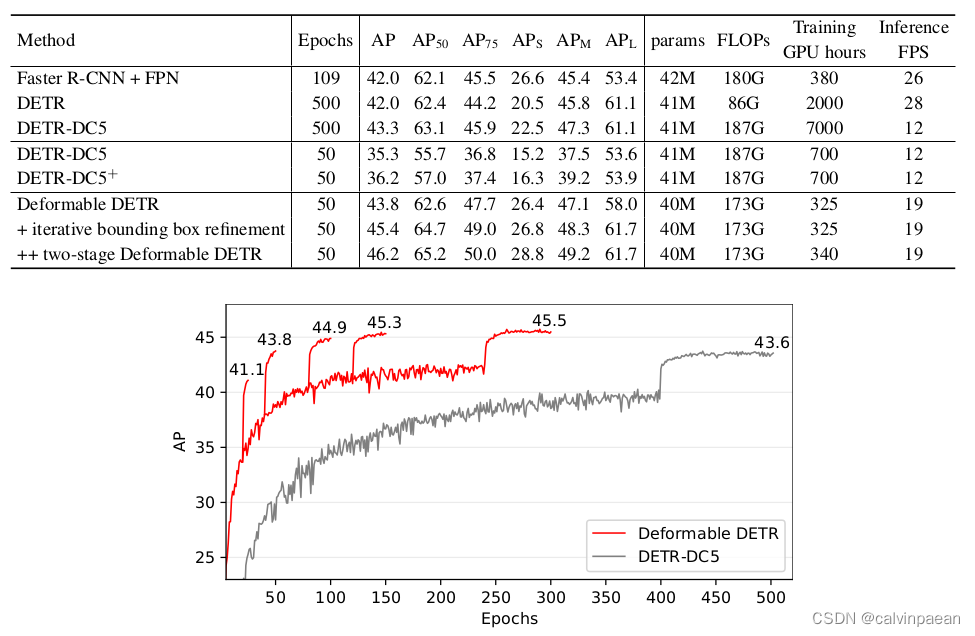
从上图可以看出，Deformable DETR 的收敛速度和表现明显优于 DETR。

3. 有什么优点？

• 将 deformable conv 和 transformer attention 结合，只关注reference point 附近少量的采样点，大幅提高了收敛速度，并保证了准确性。
• 通过 multi-scale 方式，提高了对小目标的检测效果。