KMP算法详解

什么是KMP算法

KMP算法是一种改进的字符串匹配算法，由D.E.Knuth，J.H.Morris和V.R.Pratt提出的，因此人们称它为克努特—莫里斯—普拉特操作（简称KMP算法）。KMP算法的核心是利用匹配失败后的信息，尽量减少模式串与主串的匹配次数以达到快速匹配的目的。具体实现就是通过一个next()函数实现，函数本身包含了模式串的局部匹配信息。KMP算法的时间复杂度]O(m+n) 。——百度百科

KMP算法的应用场景

• KMP算法是字符串查找的主流算法（也可以说是字符串匹配）
  • 举个具体的例子：现在有主串“abcdabcdabe”和从串”abe“，现在要求在主串中找出从串的第一个匹配项的下标（下标从 0 开始），简单点来说，就是找到从串在主串第一次出现的位置。

KMP算法和暴力求解的比较

• 暴力求解的方法我已经在实现strStr中讲过，题目如图：

  

• 具体解析过程我们不再赘述，直接看暴力求解的代码：

  int strStr(char * haystack, char * needle){
      int len_hay = strlen(haystack);
      int len_need = strlen(needle);
      if(len_need > len_hay)
          return -1;
      int i = 0,j = 0;
      int count_j = 0;
      while(1)
      {
          i = 0;	//每一次都要从字符串needle第一个字符开始匹配
          j = count_j;
          if(haystack[j] == '\0')	//如果if条件为真，就说明haystack已经遍历完，且没有出现完全匹配的情况，返回-1
              return -1;
          //将字符串needle和字符串haystack的字符逐一匹配
          while(needle[i] == haystack[j] && needle[i] != '\0' && haystack[j]!= '\0')
          {
              i++;
              j++;
          }
          //如果循环退出后needle[i]为'\0'，就说明已经完全匹配，返回第一个匹配项的下标
          if(needle[i] == '\0')
              return count_j;
          //如果未完全匹配，则从haystack的下一个字符开始重新与字符串needle进行匹配
          else
              count_j++;
      }
      return -1;
  }
  
  

• 可以发现，这种方法最坏的情况就是从串出现在主串的最后（如主串“abcdabe”，从串“abe”这种情况），因此暴力解法的时间复杂度为O(M * N)（M，N分别为主串和从串的长度）

• 而上面说到KMP算法可以将这一匹配过程的时间复杂度降为O(N + M)，极大地提高了效率。

字符串的前缀、后缀和最长相等前后缀

要理解KMP算法，首先要理解字符串前缀、后缀和最长公共前后缀这三个概念

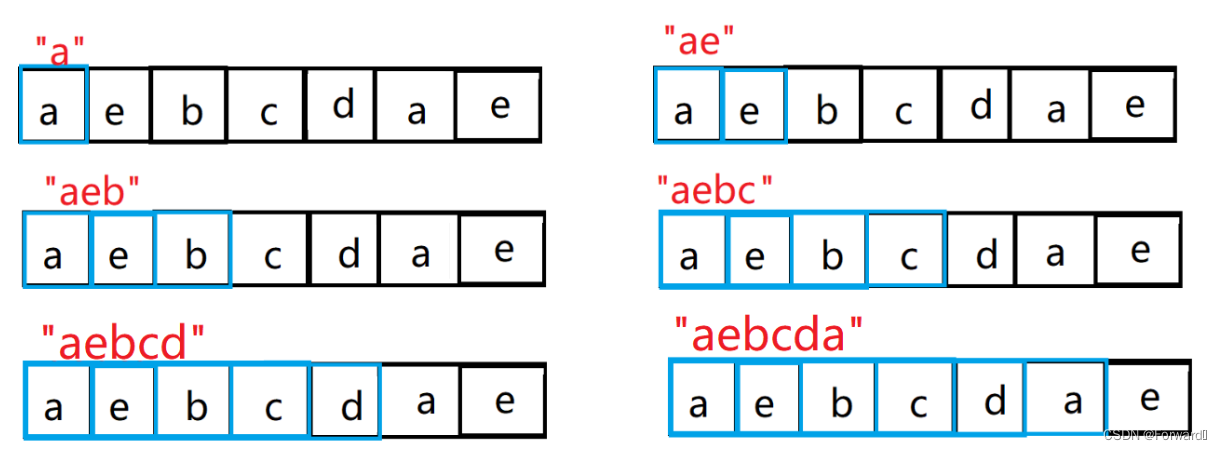
• 字符串前缀：即是指不包含最后一个字符的所有以第一个字符开头的连续子串

  • 如字符串“aebcdae”的前缀为{[a] , [ae] , [aeb] , [aebc] , [aebcd] , [aebcda]}，如图：

    

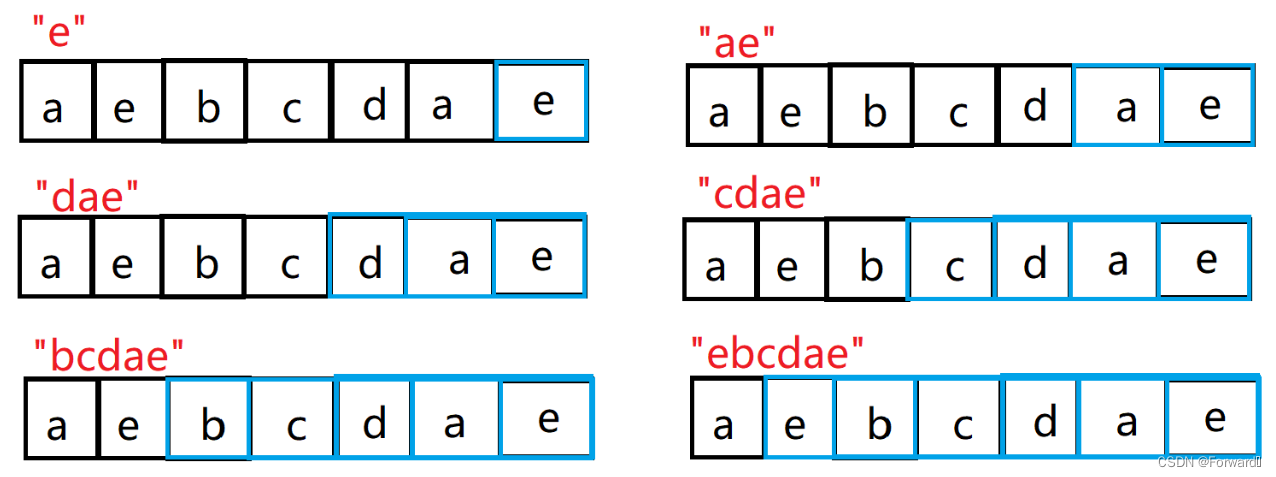
• 字符串后缀：即是指不包含第一个字符的所有以最后一个字符结尾的连续子串

  • 如字符串“aebcdae”的前缀为{[e] , [ae] , [dae] , [cdae] , [bcdae] , [ebcdae]}

    

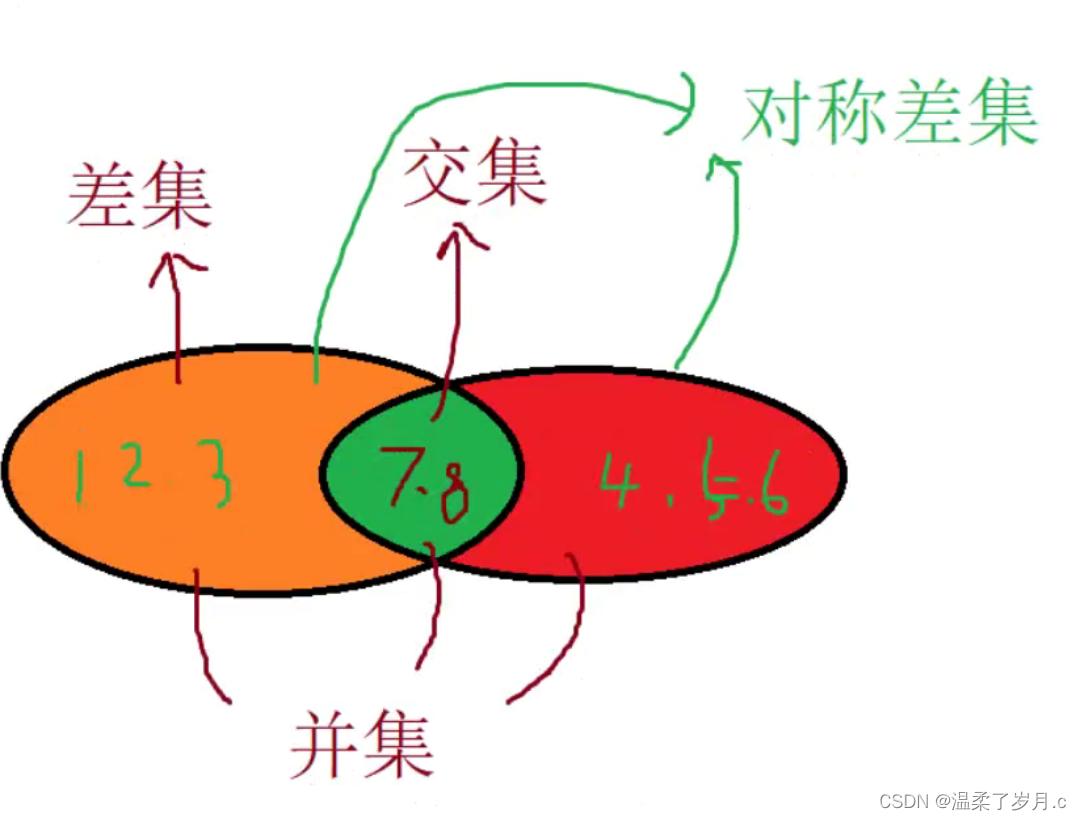
• 最长相等前后缀：即是前缀和后缀最长相等的连续子串

  • 如字符串“abcdae”的最长公共前后缀为[ae]

KMP算法实现字符串匹配的具体过程（图解）

我们以主串"abcababcabc"，从串 “abcabc”为例：

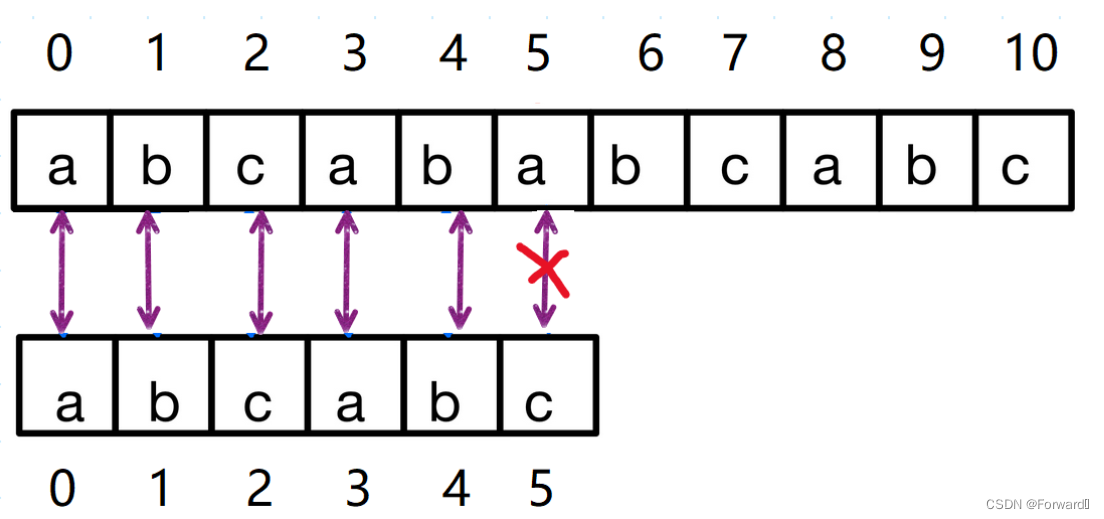
• 第一次匹配：在主串下标为5，从串下标为3时匹配失败，之后主串下标保持不变，从串下标变为为2

  

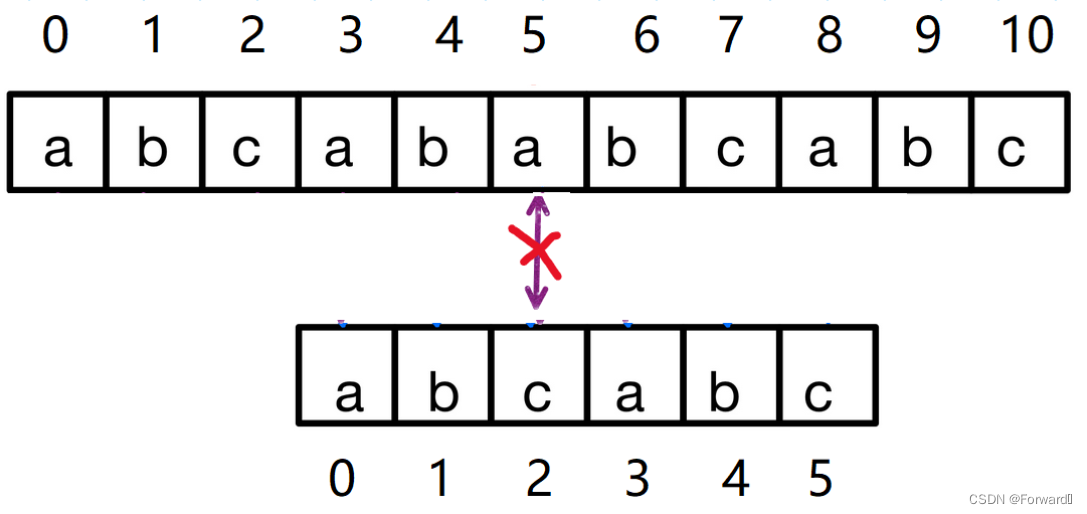
• 第二次匹配：在主串下标为5，从串下标为2处匹配失败，之后主串下标不变，从串下标变为0

  

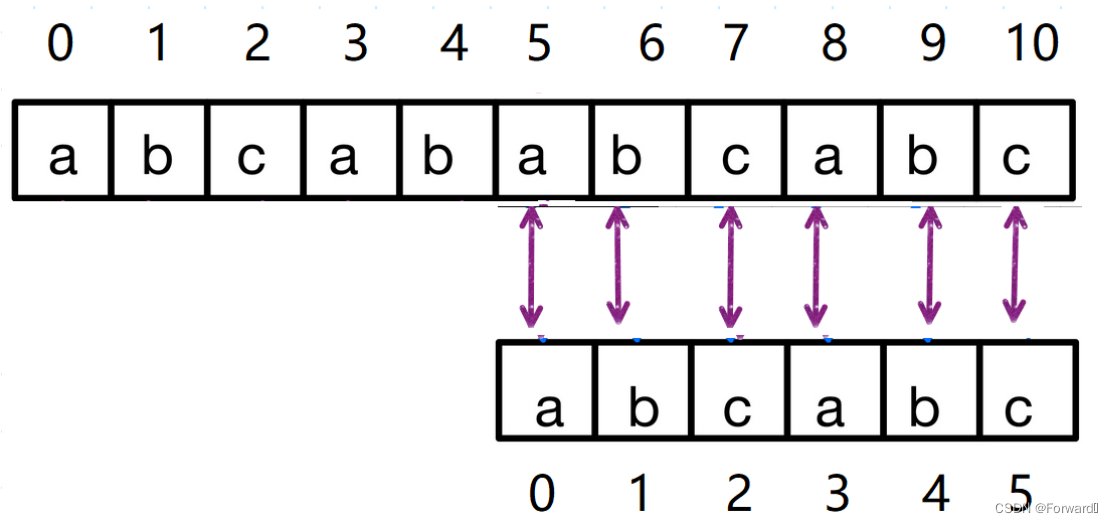
• 第三次匹配：完全匹配

  

• 看完上面KMP算法具体的匹配过程，我们可以发现，当出现不匹配的情况时，我们的从串并没有返回到第一个字符重新开始匹配，而是返回到一个特定的位置，同样，主串是停留在原处（即不匹配的字符），而不是和暴力算法一样从第一个字符到第n个字符（遍历整个主串），那么，我们如何求出从串回溯的这一特定位置呢？

从串与主串的下标变化

首先我们规定从串进行匹配时，从串字符下标为j，主串字符下标为i

先下结论:当从串在下标为j的字符匹配失败时，要使匹配效率最高，j回退的位置就是 下标为从串j字符前子串的最长相等前后缀长度 的从串元素（j为下标）。而主串下标i保持不变。

j回退的位置(从串的下标变化)

• 就拿上面的例子来说:

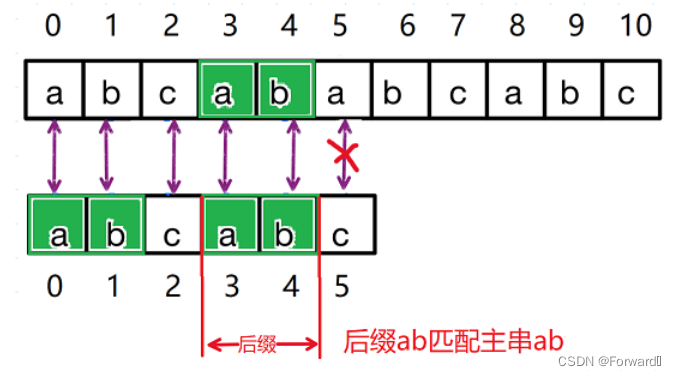
  • 在下标为5的字符（c）处匹配失败，我们将字符c前面的字符串称为子串

  • 又由图我们可以发现，子串后面的两个元素已经和主串一一对应（匹配成功）

  

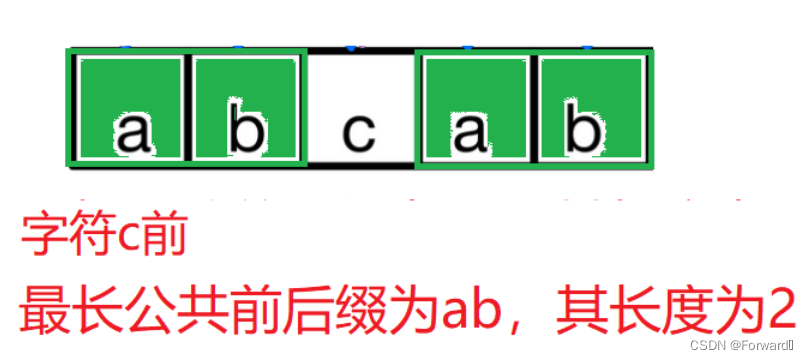
  • 而c前面子串"abcab"的最长公共前后缀为ab，其长度为2。

    

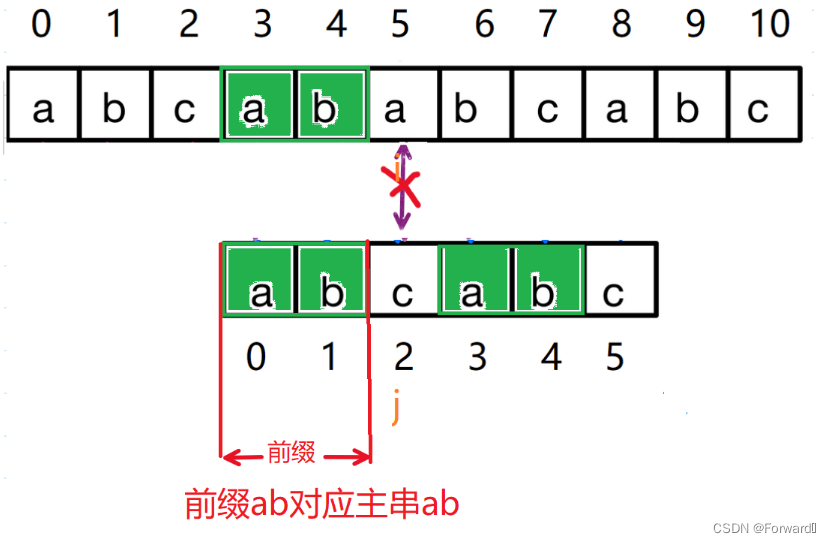
  • 将后缀ab匹配主串ab调整为前缀ab对应主串ab.

  • 即j回退到的字符就是下标为最长公相等前后缀长度的字符（即最长相等前后缀ab的后一个字符c）

    

主串的下标变化

• 为什么主串保持不变？

  • 其实道理也是一样的：

  • 主串下标为i前的两个字符已经和从串的前面两个字符一一对应（已经对从串的j进行了调整）

    

  • 那么我们就只需要继续匹配从串后面的字符和主串字符，而不需要像暴力求解一样依次遍历主串元素，从而降低了时间复杂度。

• 特殊情况:

  • 有细心的小伙伴可能会提出疑问:如果j已经回退到从串的第一个字符，但仍不能和主串匹配呢？

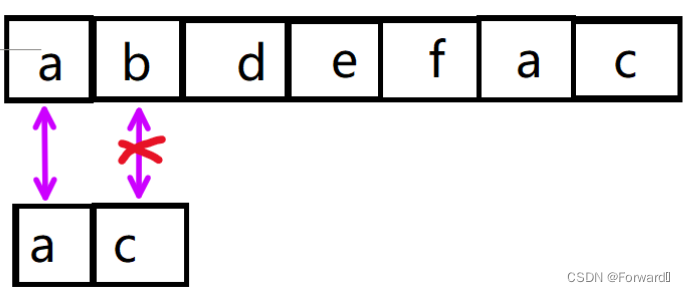
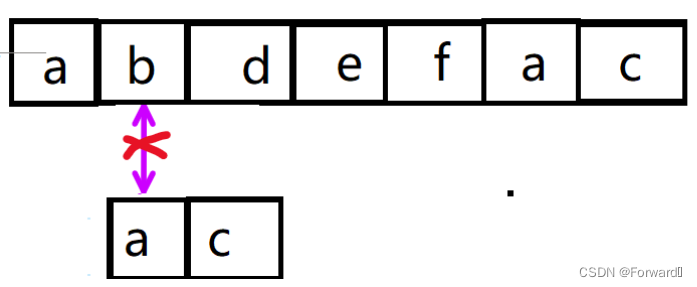
  • 我们来看一个例子：主串"abdefac"，从串"ac"。

    • 第一次匹配时，在i=1（字符b），j=1（字符c）时匹配失败

      

    • 从串字符c前的子串为a，其最大相等前后缀长度为0，因此j回退到下标为0的字符a，i不变。

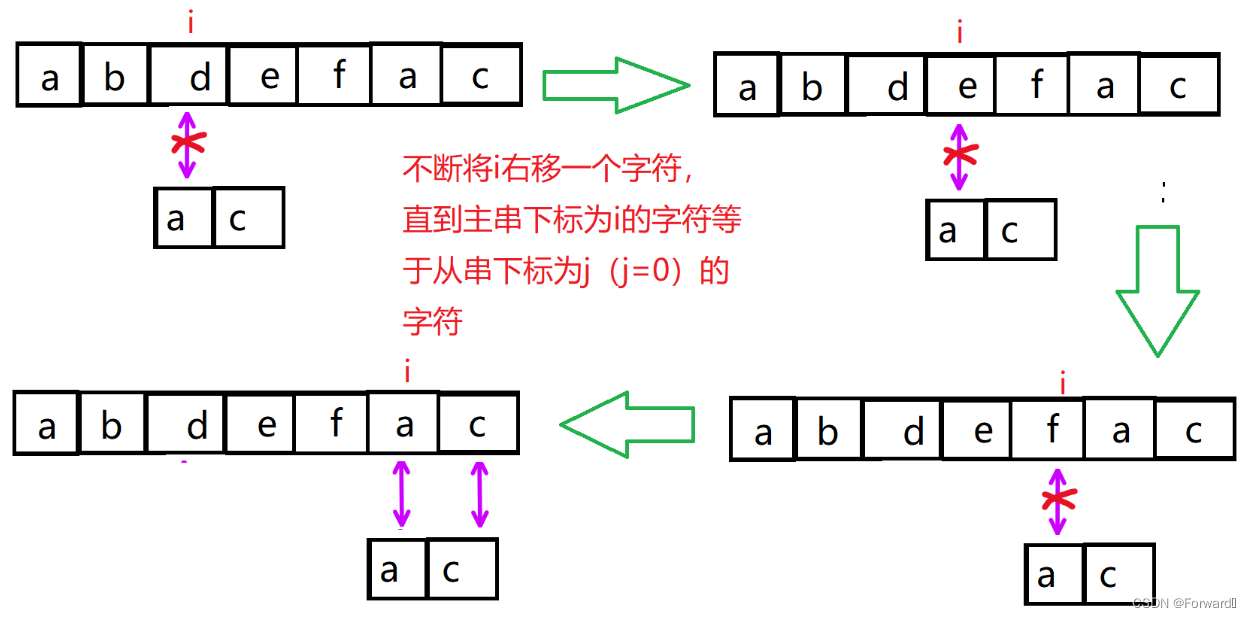
    • 第二次匹配时，在i=1（字符b），j=0（字符a）时匹配失败

      

    • 但此时j已经等于0了，已经退到不能再退了，这时我们就要移动i了，我们不断将i右移一个字符，直到主串下标为i的字符等于从串下标为j（j=0）的字符，然后再按上面的方法进行匹配。

      

Next数组

• 首先规定从串下标为j的字符前的子串的最大相等前后缀长度为k

• 我们已经知道，当主串与从串不匹配时，从串应该回退到下标为 j字符前子串的最长相等前后缀长度 的字符，而长度为length的从串（不包含结束符"\0"）有length个最长公共前后缀长度，我们规定，这length个数据都存在一个叫Next的数组中

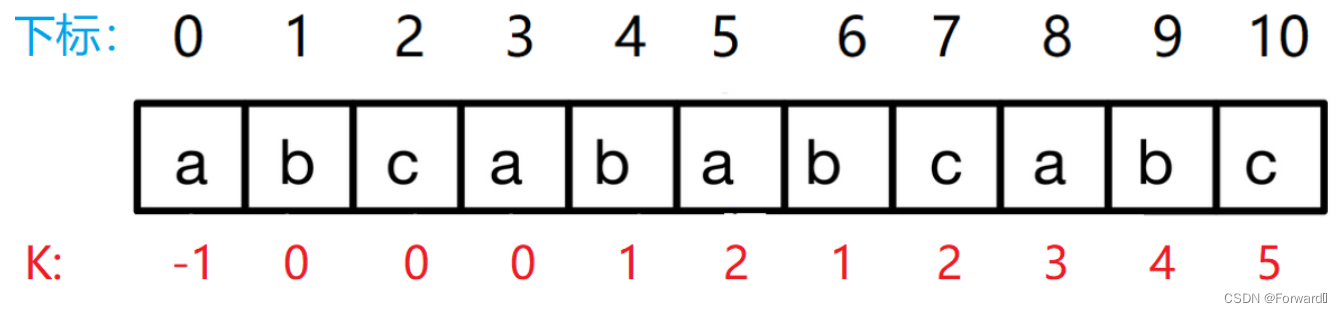
• 例如串“abcababcabc”的Next数组为{-1,0,0,0,1,2,1,2,3,4,5}，如图

  

如何运用代码逻辑计算Next数组

• 显然，用肉眼看出一个字符串的Next数组是十分简单的，但计算机可是十分死板的，那我们怎么用计算机的思维（代码逻辑）来计算Next数组呢？
• 我们还是以字符串arr“abcababcabc”为例，分以下三种情况：

arr[j] == arr[k]

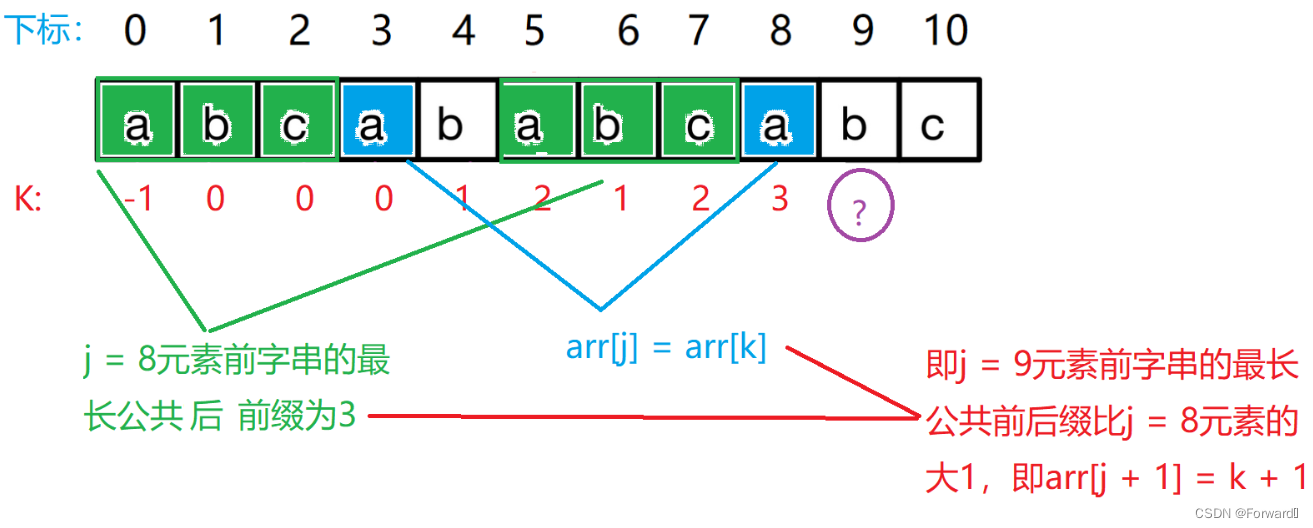
• 假设我们要计算Next[9]，其中我们已知Next[0]~Next[8] ：{-1,0,0,0,1,2,1,2,3}

• 我们可以发现当j = 8时，arr[j] = a， Next[j] = k = 3，arr[k] = a，即arr[j] = arr[k]，又因为我们已知arr[j]前子串的最长公共前后缀长度为k = 3，那么我们就可以分析出，当arr[j] == arr[k]时，Next[j + 1] = k + 1，如图：

  

arr[j] != arr[k]

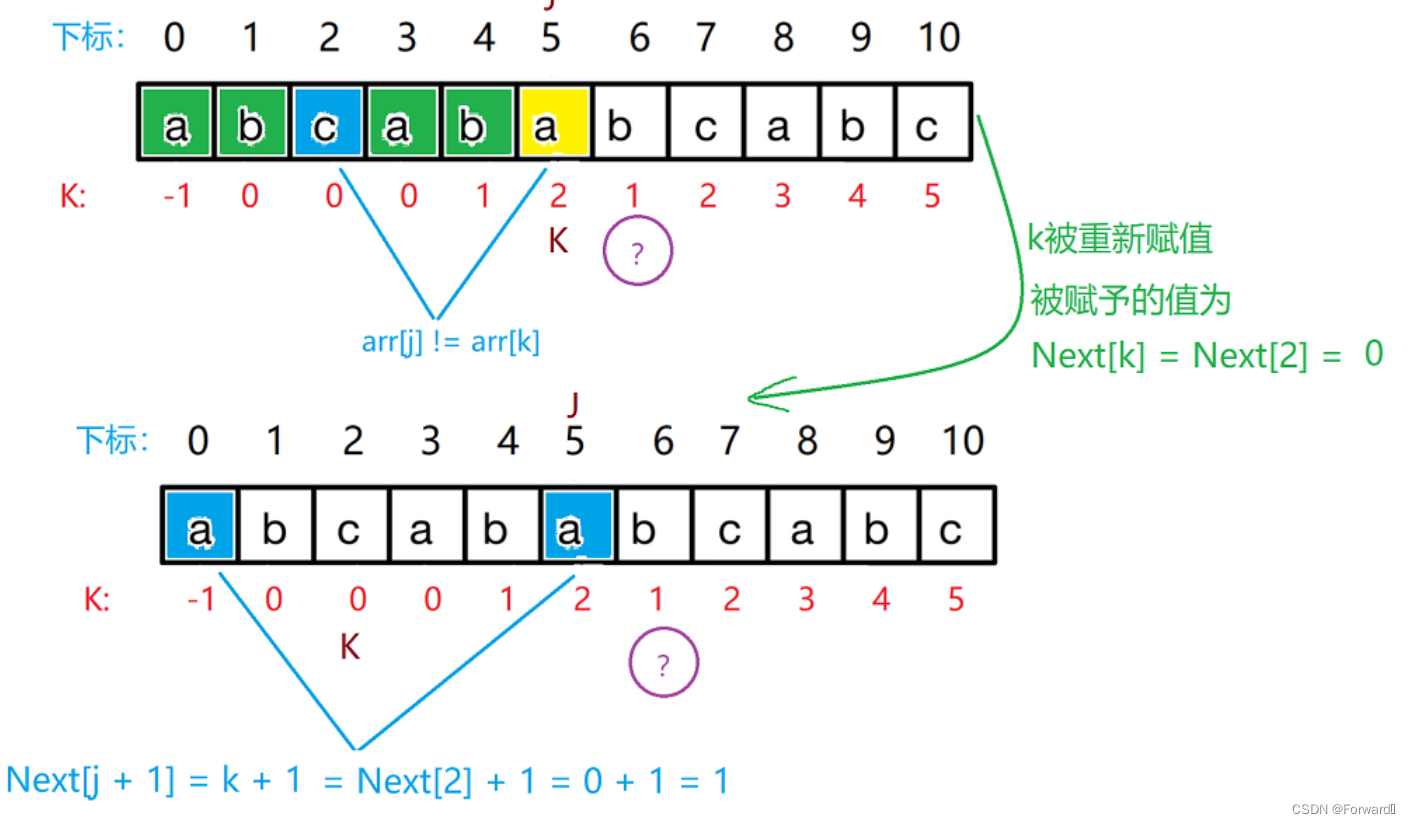
• 假设我们要计算Next[6]，其中我们知道Next[0]~Next[5] ：{-1,0,0,0,1,2}

• 当j = 5时，arr[j] = a，Next[j] = k = 2，arr[k] = c，即arr[j] != arr[k]

• 那么我们再令新的k = next[k] = 0（第一个k为新的k，第二个k还是旧的k，即Next[j]），此时arr[k] = arr[0] = a = arr[j]，这样又回到了上面arr[j] = arr[k]的条件，所以当arr[j] != arr[k]时，k就要不断回退，并被重新赋值（回退到位置就是arr[k]，被赋予的值就是Next[k]），直到出现arr[j] = arr[k]的情况

特殊情况（k == -1）

• 出现了k == -1这种情况，就意味着k走到字符串的第一个元素也没有遇到arr[j] == arr[k]的情况，那么此时k就不能继续回退了，也就是说下标为j + 1元素前子串的最长公共前后缀长度为0，即arr[j + 1] = k + 1 = -1 + 1 = 0。

得到Next数组的函数GetNext

void GetNext(int *Next, char *str)
{
    int len = strlen(str);	//从串长度
    int i = 1;		//第一个待求项Next[i]
    int k = -1;		//待求项前一个的k值
    Next[0] = -1;	//默认第一个值为-1
    while(i < len)
    {
        if(k == -1 || str[i - 1] == str[k])	//arr[j] == arr[k]和k == -1
        {
            Next[i] = k + 1;
            i++;	//待求项右移
            k++;	//待求项前一个的k值加一
            
		}
        else	//arr[j] != arr[k]
            k = Next[k];
	}
}

运用Next数组实现KMP算法

• 我们来看一道具体的题目实现strStr

  

• 直接上代码

  //得到Next数组的函数
  void GetNext(int *Next, char *str)
  {
      int len = strlen(str);	//从串长度
      int i = 1;		//第一个待求项Next[i]
      int k = -1;		//待求项前一个的k值
      Next[0] = -1;	//默认第一个值为-1
      while(i < len)
      {
          if(k == -1 || str[i - 1] == str[k])	//arr[j] == arr[k]和k == -1
          {
              Next[i] = k + 1;
              i++;	//待求项右移
              k++;	//待求项前一个的k值加一
  
  		}
          else	//arr[j] != arr[k]
              k = Next[k];
  	}
  }
  //实现字符串查找
  int strStr(char * haystack, char * needle){
      int len_hay = strlen(haystack);
      int len_need = strlen(needle);
      int i = 0, j = 0;
      //如果从串长度大于主串长度，直接返回-1
      if(len_need > len_hay)
          return -1;
      //如果主串从串长度都为0，直接返回0
      if(len_hay == 0 && len_need == 0)
          return 0;
      int *Next = (int *)malloc(sizeof(int) * len_need);	//为Next数组申请内存
      GetNext(Next,needle);	//得到Next数组
      while(i < len_hay && j < len_need)
      {
          if(haystack[i] == needle[j])
          {
              i++;
              j++;
          }
          //当j还未回溯到第一个字符
          //且从串与主串开始不匹配时，j开始回溯
          else if(j != 0)
              j = Next[j];
          //如果j已经回溯到第一个字符，那么就让主串i向右走一个字符，继续匹配
          else
              i++;
      }
      //如果j大于等于从串长度，说明j已经走到了从串为，说明匹配完成，返回主串开始匹配的位置
      if(j >= len_need)
          return i - j;
      return -1;
  }
  

对KMP算法的改进

引例：

• 我们先来看一个例子：

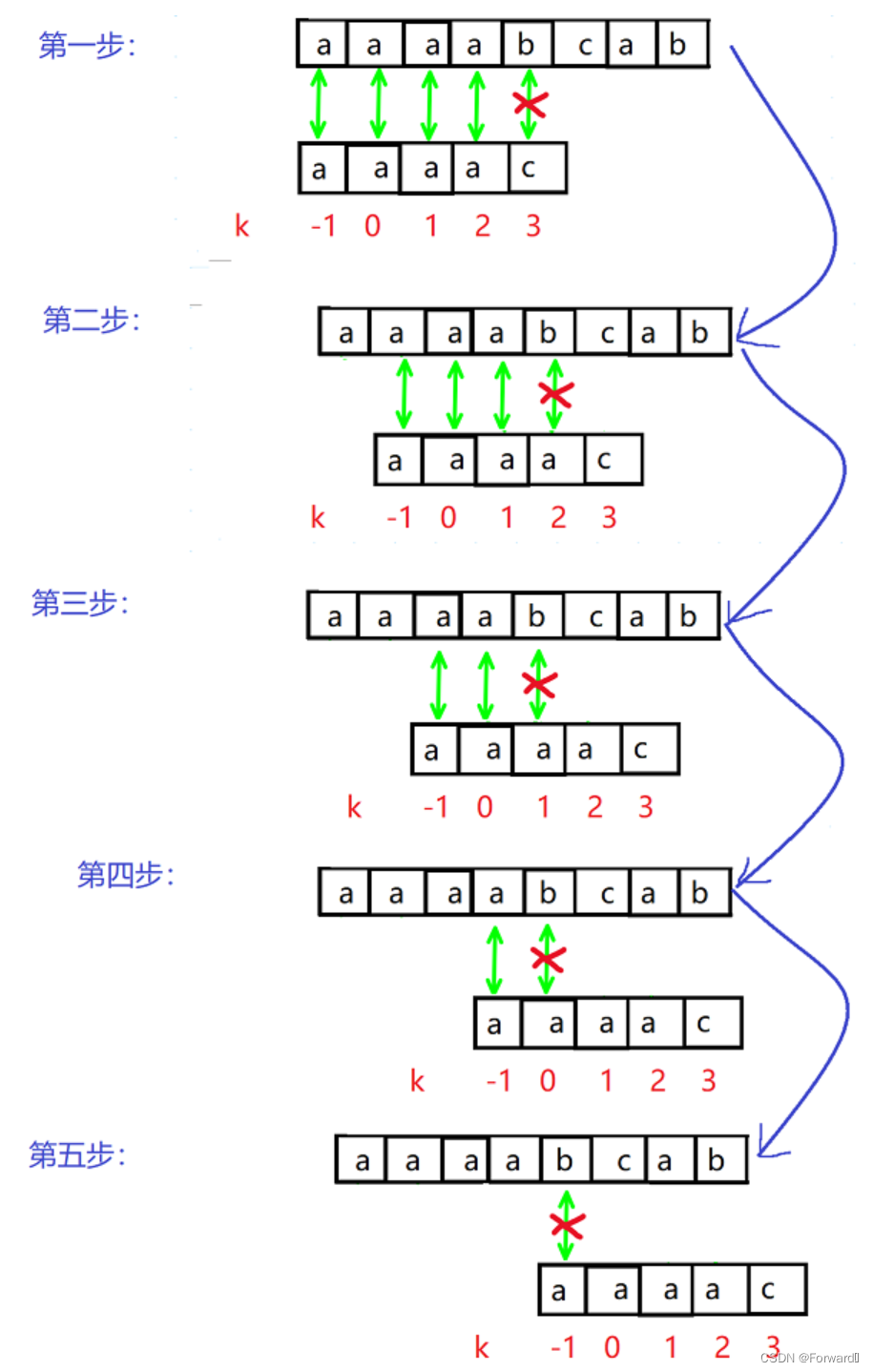
  • 主串为“aaaabcab”，从串为“aaaac”，匹配过程如图：

    

  • 我们可以发现在这一个匹配过程中，第二步，第三步，第四步其实是多余的，为什么呢？我们可以看到第一步中字符b和字符c不匹配时，字符c回溯到字符a，显然字符a仍然不和字符b匹配，但字符a回溯后的字符还是a，自然不能和字符b匹配，这样就造成了许多重复比较的情况，因此我们就是要减少这种重复比较来改善KMP算法。

改善方法

• 通过上述例子，我们知道了，出现重复比较的原因是当主串字符和从串字符出现不匹配时，从串字符的回溯字符仍等于原来的字符（arr[j] = arr[k]）
• 因此我们就要阻止这种情况的出现，若从串字符的回溯字符仍等于从串字符，那么就要继续回溯（next[i] = next[k]），直到出现不相等的情况或回溯到了从串头
• 自然，我们对next数组的求法也要做出改变。
  • 例如字符串“ababaaab”的next数组为{-1,0,-1,0,-1,3,1,0}
    

实现代码

//得到新的Next数组Nextval
void GetNextVal(int* nextval, char *str)
{
	int len = strlen(str);
	int k = -1;
	int i = 0;
	nextval[0] = -1;	//第一个k值默认为-1
    //由于操作是先++后赋值，因此为了不会数组越界，i < len - 1
	while (i < len - 1)
	{
		if (k == -1 || str[i] == str[k])
		{
			i++;
			k++;
            //相比于最开始的KMP算法，多出来的就是这个if判断
            //如果回溯字符等于原字符，那么就要继续回溯，避免重复比较
			if (str[i] == str[k])
				nextval[i] = nextval[k];
            //如果回溯字符不等于原字符，那么就和原来的操作一样
			else
				nextval[i] = k;
		}
		else
			k = nextval[k];
	}
}

int strStr(char* hayStack, char* needle)
{
	int len_h = strlen(hayStack);
	int len_n = strlen(needle);
	int i = 0, j = 0;
	int *NextVal = (int*)malloc(sizeof(int) * len_n);
	GetNextVal(NextVal, needle);
	while (i < len_h && j < len_n)
	{
		if (hayStack[i] == needle[j])
		{
			i++;
			j++;
		}
		else if (j != 0)
		{
			j = NextVal[j];
            //相比于原来的KMP算法，多出了这一句if判断
            //这是由于新的NextVal数组由于k的多次回溯，会出现不止第一个字符的k为-1的情况，因此为防止数组越界，当j为-1时要将其置为零
			if (j == -1)
				j = 0;
		}
		else
			i++;
	}
	if (j >= len_n)
		return i - j;
	else
		return -1;
}