记录常规的完全背包问题模型
- 1.暴力dfs
- 2.优化dfs,记忆化dfs
- 3.动态规划
- 4.bfs
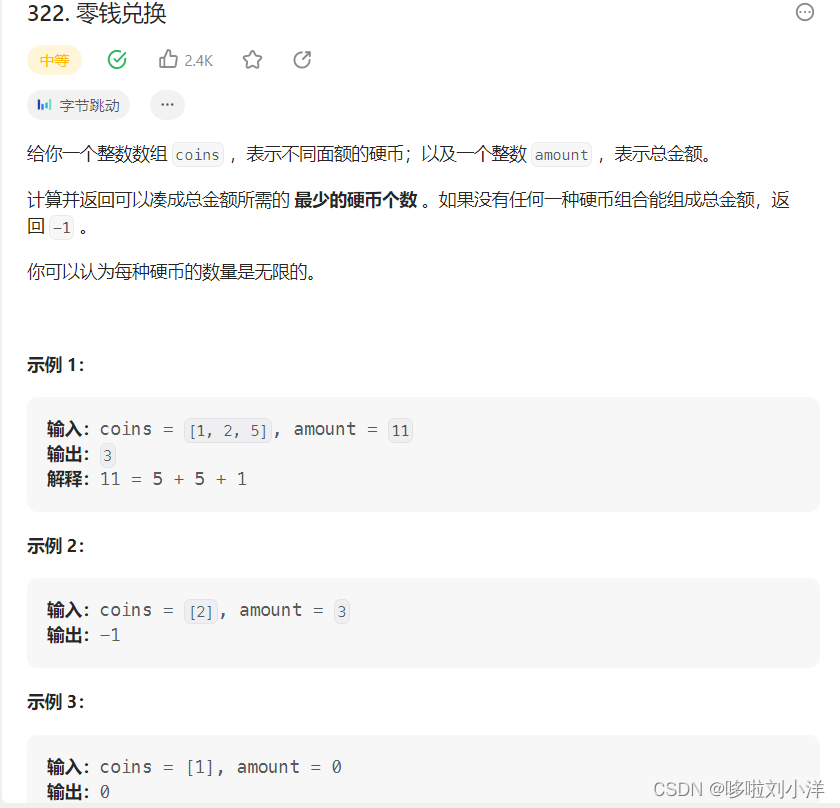
1.由于每件物品可以无限取,那么可以发现这是一个完全背包问题模型。
1.暴力dfs
最后要求的是:n种硬币,凑成总金额为amount。每种硬币无限取,最少需要多少枚硬币?
那么根据问题来写递归:
class Solution
{
public:
int coinChange(vector<int>& coins, int amount)
{
int n=coins.size();
//dfs(i)表示剩余价值为i使用硬币的最少数量
function<int(int)>dfs=[&](int amount)->int
{
if(amount<0)return -1;
if(amount==0)return 0;
int Min=0x3f3f3f3f;
for(int i=0;i<n;i++)
{
int t=dfs(amount-coins[i]);
if(t>=0&&Min>t)Min=t+1;
}
return Min;
};
int ans=dfs(amount);
return ans==0x3f3f3f3f?-1:ans;
}
};
2.优化dfs,记忆化dfs
因为递归存在大量重复,所以使用记忆化优化
class Solution
{
public:
int coinChange(vector<int>& coins, int amount)
{
int n=coins.size();
int memo[10010];
memset(memo,0,sizeof memo);
function<int(int)>dfs=[&](int amount)->int //剩余价值为amount时最少需要的硬币数量
{
if(amount<0)return -1;
if(amount==0) return 0;
if(memo[amount]!=0)return memo[amount];
int Min=0x3f3f3f3f;
for(int i=0;i<n;i++)
{
int t=dfs(amount-coins[i]);
if(t>=0&&t<Min)Min=t+1;
}
memo[amount]=Min;
return Min;
};
int ans=dfs(amount);
return ans==0x3f3f3f3f?-1:ans;
}
};
3.动态规划
动态规划是这道题最常规的做法。那么直接拿出模板
class Solution
{
public:
int coinChange(vector<int>& coins, int amount)
{
int n=coins.size();
int dp[13][10010]; //dp[i][j]表示前i种硬币,组成价值为amount的最少硬币数量
memset(dp,0x3f,sizeof dp);
for(int i=0;i<=n;i++)
dp[i][0]=0;
for(int i=1;i<=n;i++) //枚举物品
{
int v=coins[i-1];
for(int j=0;j<=amount;j++) //枚举体积
{
for(int k=0;k*v<=j;k++) //枚举当前物品的数量
{
dp[i][j]=min(dp[i][j],dp[i-1][j-k*v]+k);
}
}
}
return dp[n][amount]==0x3f3f3f3f?-1:dp[n][amount];
}
};
优化很简单,看下面:

class Solution
{
public:
int coinChange(vector<int>& coins, int amount)
{
int n=coins.size();
int dp[13][10010]; //dp[i][j]表示前i种硬币,组成价值为amount的最少硬币数量
memset(dp,0x3f,sizeof dp);
for(int i=0;i<=n;i++)
dp[i][0]=0;
for(int i=1;i<=n;i++) //枚举物品
{
for(int j=0;j<=amount;j++)
{
dp[i][j]=dp[i-1][j];
if(j-coins[i-1]>=0)
dp[i][j]=min(dp[i][j],dp[i][j-coins[i-1]]+1);
}
}
return dp[n][amount]==0x3f3f3f3f?-1:dp[n][amount];
}
};
实际上到这一步已经很完善了,但是空间上可以继续优化一下,二维优化为一维
class Solution
{
public:
int coinChange(vector<int>& coins, int amount)
{
int n=coins.size();
int dp[10010]; //dp[i][j]表示前i种硬币,组成价值为amount的最少硬币数量
memset(dp,0x3f,sizeof dp);
dp[0]=0; //dp[i][0]
for(int i=1;i<=n;i++) //枚举物品
{
for(int j=coins[i-1];j<=amount;j++)
{
//dp[i][j]=dp[i-1][j];
dp[j]=min(dp[j],dp[j-coins[i-1]]+1);
}
}
return dp[amount]==0x3f3f3f3f?-1:dp[amount];
}
};
这里一维版本为什么第二个for循环不需要逆序呢?看公式:
d
p
[
i
]
[
j
]
=
m
i
n
(
d
p
[
i
]
[
j
]
,
d
p
[
i
]
[
j
−
c
o
i
n
s
[
i
−
1
]
]
+
1
)
;
dp[i][j]=min(dp[i][j],dp[i][j-coins[i-1]]+1);
dp[i][j]=min(dp[i][j],dp[i][j−coins[i−1]]+1);没有数据污染,更新的dp不会造成影响后续更新。
4.bfs
由于是求最少,那么可以抽象成最短路问题。先对硬币排序,然后一步步向四周扩散。3
class Solution
{
public:
int coinChange(vector<int>& coins, int amount)
{
sort(coins.begin(), coins.end(), greater<int>());// 剪枝,首先减去大数再减去小数
queue<int> q;
q.push(amount);
unordered_set<int> vis;
vis.insert(amount);
int ans = 0;
while (!q.empty()) {
int size = q.size();
while (size --) {
int top = q.front();
q.pop();
if (top == 0) return ans;// 当amount已经减到0就返回广搜的层数
for (int i = 0; i < coins.size(); i ++) {
int num = top - coins[i];
if (!vis.count(num) && num >= 0) {
vis.insert(num);
q.push(num);
}
}
}
ans ++;
}
return -1;
}
};

![[NodeJS] 优缺点及适用场景讨论](https://img-blog.csdnimg.cn/img_convert/fa16e0aff372bfee5239b1863c1ec8cc.png)