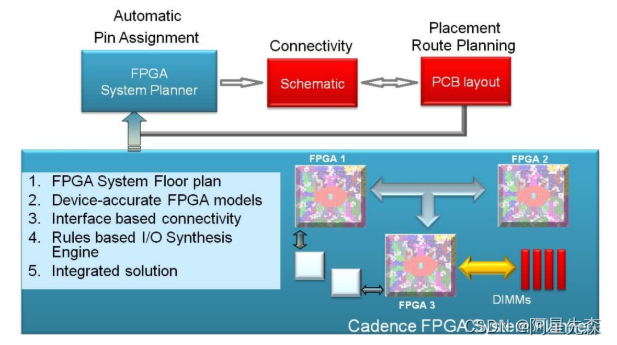
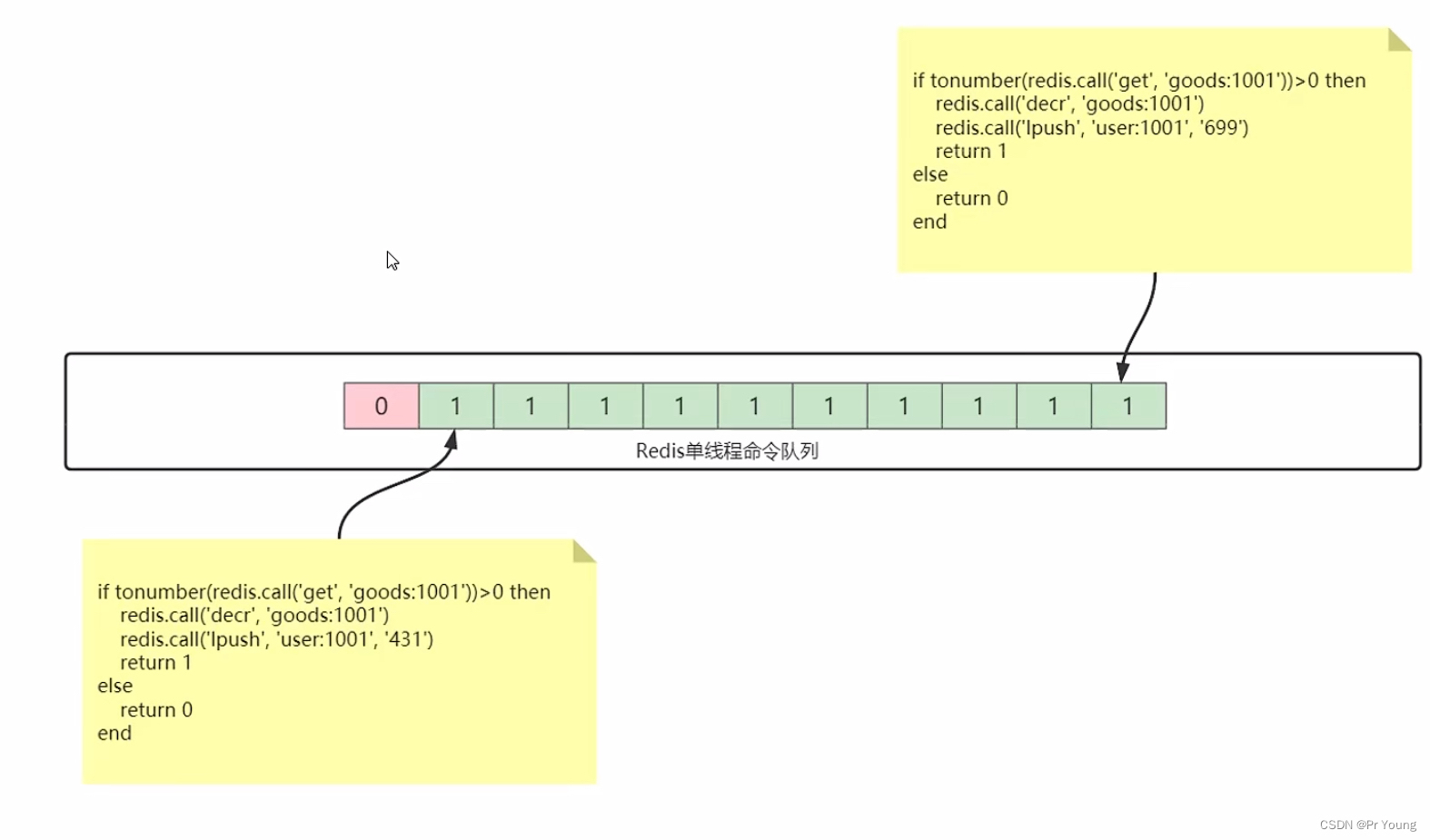
浅过二次型

理解二次型可以从二次型的多项式入手：

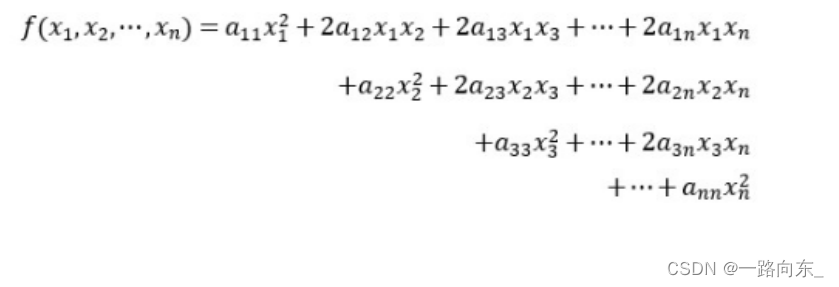
 显然，在系数都为实数的情况下，二次型矩阵即为一个实对称矩阵。

取一个代入值的例子就是：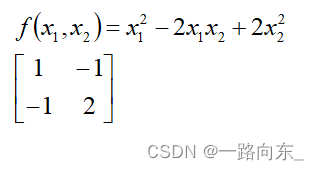

二次型的标准型

OK，再从二次型的标准型的多项式入手，如下，可以看出，标准型就是把未知数都变成平方的样子。

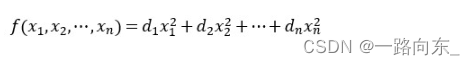
显然，此时的二次型矩阵变为对角矩阵：

求得的方法非常简单——特征根法，

所求的特征根就是对角元素值。

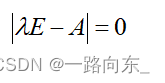
二次型的规范型

其实就是在二次型的标准型基础上，做非奇异变换，把系数换为1或-1（符号依赖于原先是否为正负，即原先为正那么最后系数为1，原先为负，那么最后系数为-1）。

相当于变成：

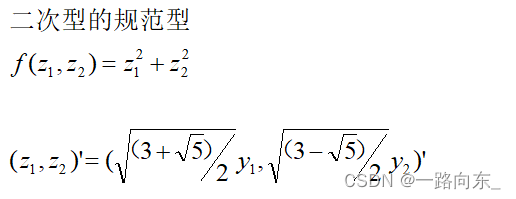
 速通

（1）知二次型，设二次型对称矩阵A，求A。

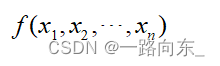
（2）特征根法，|λE - A| = 0得二次型标准型

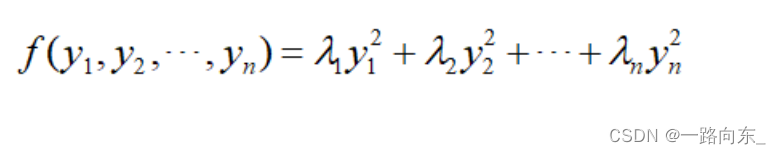
 （3）非奇异变换，简单理解为将标准型系数化为±1 => 规范型

如下，假设λ1为负数，其他λ都为正数。

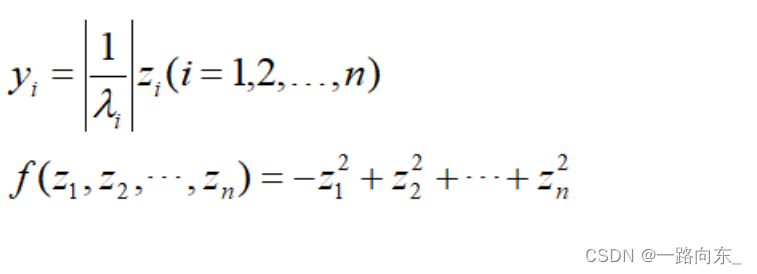
 篇幅限制，关于二次型矩阵合同与秩的性质待描述。