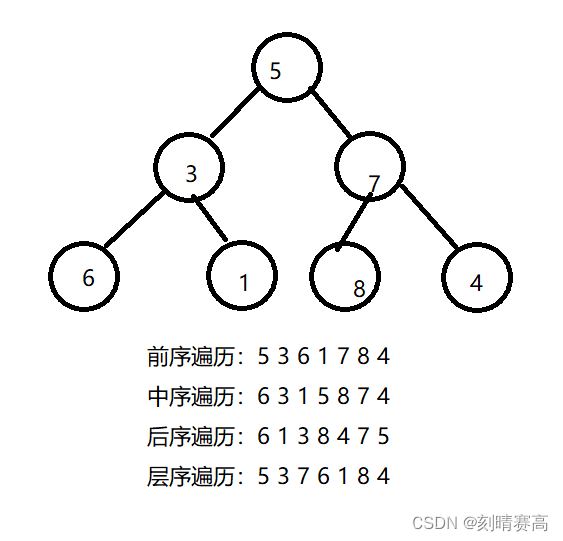
既然要认识二叉树,自然要知道二叉树的基本操作。首先最基本的是要知道二叉树的遍历,所谓遍历(Traversal)是指沿着某条搜索路线,依次对树中每个结点均做一次且仅做一次访问。访问结点所做的操作依赖于具体的应用问题(比如:打印节点内容、节点内容加1)。 遍历是二叉树上最重要的操作之一,是二叉树上进行其它运算之基础。在遍历二叉树时,如果没有进行某种约定,每个人都按照自己的方式遍历,得出的结果就比较混乱,如果按照某种规则进行约定,则每个人对于同一棵树的遍历结果肯定是相同的。如果N代表根节点,L代表根节点的左子树,R代表根节点的右子树,则根据遍历根节点的先后次序有以下遍历方式:
我们虽然已经知道了二叉树的遍历,但是我们还是不知道它是如何实现遍历的,别急,现在我们就开始学习如何遍历二叉树。
前序遍历:
既然要前序遍历。那么我们得从根节点开始,先进行打印,然后向它的左树开始前进,而到了它的左树后,则该节点又可以认为是一个根节点(毕竟它下面还有节点,也可以当成是一颗树的根),然后则开始重复上述操作,当我们遍历到null怎么办?当我们遍历到null然后就返回它的父节点,然后往它的父节点的右树继续走,再重复就行。听起来是不是要使用循环或是递归,对,你猜的没错,不过相比循环,递归更简单,所以我们先写递归版。
public void preOrder(TreeNode root) {
if (root == null){
return;
}
System.out.print(root.val + " ");
preOrder(root.left);
preOrder(root.right);
}//根据代码画图会更好理解。
中序遍历:
中序遍历与前序遍历差不多,只不过它的访问顺序不同罢了,因此我们只需将打印的代码放在稍后面就行。
void inOrder(TreeNode root) {
if (root == null){
return;
}
inOrder(root.left);
System.out.print(root.val + " ");
inOrder(root.right);
}
后序遍历:
后序遍历也是如此。
void postOrder(TreeNode root) {
if (root == null){
return;
}
postOrder(root.left);
postOrder(root.right);
System.out.print(root.val + " ");
}
前中后遍历相差不大,那么层序遍历也是如此吗?不,与之相比,层序遍历较难,要想层序遍历,我们就得知道它的遍历方式,它是自上而下,从左往右的,因此我们可以创建一个队列,然后将根节点放进去,我们每次都删除一个,并且打印删除的,然后将它的左子树和右子树放进去就行,直到队列为空为止。
void levelOrder(TreeNode root) {
if (root == null){
return;
}
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
while(!queue.isEmpty()){
TreeNode tmp = queue.poll();
if (tmp != null){
System.out.print(tmp.val + " ");
queue.offer(tmp.left);
queue.offer(tmp.right);
}
}
}
写完前中后递归遍历后,我们该写非递归版,与递归相比,非递归的性能就差上不少,并且要用到栈,但是我们不能因为它的性能差就不学是吧?我们至少得知道它是如何做到的吧。当然,我们现在就开始它的非递归道路,首先前序遍历,我们需要遍历到它的最左那颗树上,这并不难,我们只需要运用循环一直往左子树走就行,直到左子树为null,难的是我们如何回到它的父节点和父节点的右子树去,而这就需要运用到栈,我们可以将前往最左子树的路径放到栈里面,当我们遍历到null,说明左子树到底了,然后我们就删除栈顶元素,而这个元素恰好是其父节点,然后我们将其转到右子树去,再重复上述操作,这样就能遍历到所有的元素了。
public void preOrderNol(TreeNode root){
Stack<TreeNode> stack = new Stack<>();
if (root == null){
return;
}
TreeNode cur = root;
while (!stack.isEmpty() || cur != null){
while (cur != null){
stack.push(cur);
System.out.print(cur.val + " ");
cur = cur.left;
}
TreeNode node = stack.pop();
cur = node.right;
}
}
而中序遍历与之相同,不过打印的位置不同罢了,就如递归版一样。
void inOrderNo(TreeNode root){
Stack<TreeNode> stack = new Stack<>();
if (root == null){
return;
}
TreeNode cur = root;
while (!stack.isEmpty() || cur != null){
while (cur != null){
stack.push(cur);
cur = cur.left;
}
TreeNode node = stack.pop();
System.out.print(cur.val + " ");
cur = node.right;
}
}
但后序遍历则不同,它考虑的要更多,但是方法与前序和中序遍历一样,感兴趣的可以自己去实现。