1049.最后一块石头的重量 II
讲解链接:代码随想录-1049.最后一块石头的重量 II
- 确定 dp 数组以及下标的含义:dp[j]表示容量(这里说容量更形象,其实就是重量)为 j 的背包,最多可以背最大重量为 dp[j]。
石头的重量是 stones[i],石头的价值也是 stones[i] ,可以 “最多可以装的价值为 dp[j]” == “最多可以背的重量为 dp[j]” - 确定递推公式:dp[j] = max(dp[j], dp[j - stones[i]] + stones[i]);
- dp 数组如何初始化:既然 dp[j]中的 j 表示容量,那么最大容量(重量)是多少呢,就是所有石头的重量和。而我们要求的 target 其实只是最大重量的一半。计算出石头总重量 然后除 2,得到 dp 数组的大小。
- 确定遍历顺序:物品遍历的 for 循环放在外层,遍历背包的 for 循环放在内层,且内层 for 循环倒序遍历!
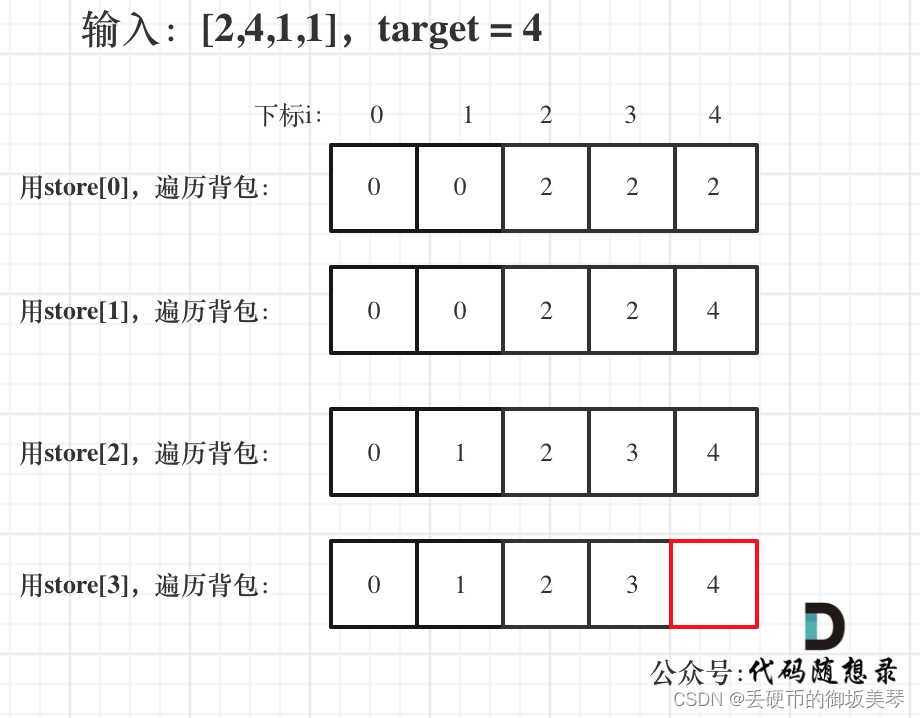
- 举例推导 dp 数组:举例,输入:[2,4,1,1],此时 target = (2 + 4 + 1 + 1)/2 = 4 ,dp 数组状态图如下:
public int lastStoneWeightII(int[] stones) {
int sum = Arrays.stream(stones).sum();
int target = sum / 2;
int[] dp = new int[target + 1];
for (int i = 0; i < stones.length; i++) {
for (int j = target; j >= stones[i]; j--) {
dp[j] = Math.max(dp[j], dp[j - stones[i]] + stones[i]);
}
}
return sum - dp[target] - dp[target];
}
494.目标和
讲解链接:代码随想录-494.目标和
动态规划-01 背包
我们可以把集合分成两个,一个用来存放正数的,一个用来存放负数的。
正数集合和 减去 负数集合和 = 目标值。那么 正数集合和 = (目标值 + 总集合和) / 2; 推导过程就不放在这里了。
此时我们只需要让集合中的数可以凑出正数集合和,就说明是一种方法。
-
确定 dp 数组以及下标的含义:dp[j] 表示:填满 j(包括 j)这么大容积的包,有 dp[j]种方法
-
确定递推公式: 只要搞到 nums[i],凑成 dp[j]就有 dp[j - nums[i]] 种方法。
- 举例:nums : [1, 2, 3, 4, 5] ; target : 5 。
- 解释:这里 dp 的数组长度为 11,下标到 10,说明只有正数集合和为 10 的时候,才能满足目标值。所以 dp[10] 的值就是集合中的数能组成和为 10 的组合数量。
- 打印 :
-
dp下标 0,1,2,3,4,5,6,7,8,9,10 i : 0, nums[i] : 1, dp : [1,1,0,0,0,0,0,0,0,0,0] 因为nums[0] = 1,所以这个集合和等于 1 的组合只有 1 种,所以 dp[1] = 1; i : 1, nums[i] : 2, dp : [1,1,1,1,0,0,0,0,0,0,0] nums[1] = 2,此时能组成 2 的组合有 1 种,和为 3 的集合有 1 种[1,2]。所以 dp[2] = 1, dp[3] = 1。 i : 2, nums[i] : 3, dp : [1,1,1,2,1,1,1,0,0,0,0] nums[2] = 3,此时组成 3 的组合多了 1 种,最大能组成的和到 6。 i : 3, nums[i] : 4, dp : [1,1,1,2,2,2,2,2,1,1,1] 下面依次类推。 i : 4, nums[i] : 5, dp : [1,1,1,2,2,3,3,3,3,3,3] - 上面的举例主要验证了公式和的正确性,那么为什么递推公式是:
dp[j] += dp[j - nums[i]]; - 当背包容量(集合和)为 10 的时候,当前物品的价值为 4 时,我们有的组合就是:背包容量为 6 的组合数。
当背包容量(集合和)为 10 的时候,当前物品的价值为 5 时,我们有的组合就是:背包容量为 5 的组合数 加上 之前已经得到的组合数。
public int findTargetSumWays(int[] nums, int target) {
int sum = Arrays.stream(nums).sum();
if ((target + sum) % 2 == 1 || Math.abs(target) > sum) {
return 0; // 此时没有方案
}
int bagSize = (target + sum) / 2;
int[] dp = new int[bagSize + 1];
dp[0] = 1;
for (int i = 0; i < nums.length; i++) {
for (int j = bagSize; j >= nums[i]; j--) {
dp[j] += dp[j - nums[i]];
}
}
return dp[bagSize];
}
回溯算法(会超时)
提示回溯,但是用回溯会超时,这个回溯方法可以只求正数集合和来简化一下。
class FindTargetSumWays {
public static void main(String[] args) {
int[] num = ArrayUtils.initArray(0, 0, 0, 0, 0, 0, 0, 0, 1);
int target = 1;
int targetSumWays = new FindTargetSumWays().findTargetSumWays(num, target);
System.out.println(targetSumWays);
}
Integer count = 0;
public int findTargetSumWays(int[] nums, int target) {
backtracking(nums, target, 0, new ArrayList<>());
return count;
}
void backtracking(int[] nums, int target, int start, List<Integer> paths) {
if (paths.size() == nums.length) {
if (paths.stream().reduce(Integer::sum).get() == target) {
count++;
}
return;
}
for (int i = start; i < nums.length; i++) {
paths.add(nums[i]);
backtracking(nums, target, i + 1, paths);
paths.remove(paths.size() - 1);
paths.add(-nums[i]);
backtracking(nums, target, i + 1, paths);
paths.remove(paths.size() - 1);
}
}
}
474.一和零
讲解链接:代码随想录-474.一和零
- 确定 dp 数组以及下标的含义:dp[i][j]:最多有 i 个 0 和 j 个 1 的 strs 的最大子集的大小为 dp[i][j]。
- 确定递推公式:dp[i][j] 可以由前一个 strs 里的字符串推导出来,strs 里的字符串有 zeroNum 个 0,oneNum 个 1。dp[i][j] 就可以是
dp[i - zeroNum][j - oneNum] + 1。然后我们在遍历的过程中,取 dp[i][j] 的最大值。
所以递推公式:dp[i][j] = max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1);
public int findMaxForm(String[] strs, int m, int n) {
int[][] dp = new int[m + 1][n + 1];
for (String str : strs) {
int zeroNum = 0;
int oneNum = 0;
for (char c : str.toCharArray()) {
if (c == '0') zeroNum++;
else oneNum++;
}
for (int i = m; i >= zeroNum; i--) {
for (int j = n; j >= oneNum; j--) {
dp[i][j] = Math.max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1);
}
}
}
return dp[m][n];
}