在统计学中，假设检验是评估某种特定情况下观察到的数据是否符合假设的一种方法。t检验和Z检验是两种常用的假设检验方法，分别用于比较均值差异以及比例差异。在医学统计中，t检验和Z检验经常被用于研究和比较不同治疗方法的效果，例如药物疗效、手术效果等。t检验和Z检验应用起来容易混淆，下面介绍下它们的区别。

一、t检验

t检验是用于比较两个总体的均值之间是否存在显著差异。在进行t检验时，不知道总体的标准差，而是使用样本标准差代替。t检验基于t分布，其形状与正态分布相似，但是在尾部较厚。随着样本量的增加，t分布逐渐接近正态分布。

t检验通常用于以下场景：1.比较两个独立样本的均值；2.比较两个配对样本的均值差异；3.验证样本均值与已知的总体均值之间是否存在显著差异；4.分析某一变量的变化是否显著。

实例1

以往通过大规模调查已知某地新生儿平均出生体重为3.30kg，从该地难产儿中随机抽取35名新生儿作为研究样本，平均出生体重为3.42kg，标准差为0.40kg，问该地难产儿出生体重与一般新生儿体重有无差异？

二、Z检验

Z检验又叫U检验，通常用于检验两个总体的均值或比例之间是否存在显著差异。在进行Z检验时，假设观察到的数据是正态分布的，并且已知总体的标准差。当已知总体标准差时，我们可以利用Z统计量进行假设检验。

Z检验通常用于以下场景：1.比较两个总体的均值或比例；2.验证样本均值或比例与已知的总体均值或比例之间是否存在显著差异；3.分析某一变量的变化是否显著。

实例2：

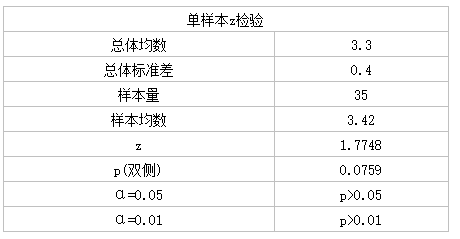
以往通过大规模调查已知某地新生儿平均出生体重为3.30kg，标准差为0.40kg，从该地难产儿中随机抽取35名新生儿作为研究样本，平均出生体重为3.42kg，问该地难产儿出生体重与一般新生儿体重有无差异？

三、关键区别

1.在已知总体标准差的情况下，使用Z检验；在未知总体标准差的情况下，使用t检验。

2.t检验基于t分布，而Z检验基于正态分布。随着样本量的增加，t分布逐渐接近正态分布。

3.在样本量较小（通常小于30）且总体分布近似正态时，t检验比Z检验更为适用。

4.在样本量较大时，t检验和Z检验的结果通常是非常接近的。

(t检验与Z检验的区别 - 天兰统计-医学统计助手★卡方检验,t检验,F检验,秩和检验,方差分析)