1. 位操作符综述

位操作有逻辑运算和移位运算，如位与、位或、位取反、按位异或、移位等操作。位运算通常会和底层代码寄存器的操作结合在一起使用，比如想要让寄存器中的任意1位或者任意几位位设置为1，或者设置为0，从而实现对寄存器位的控制。

1.1 位与 &

真值表：Y = A + B

A	B	Y
0	0	0
0	1	0
1	0	0
1	1	1

特点：同一二进制位上，只有1和1进行与运算，其结果才为1，其余全是0。

该特点可以对特定的二进制位清0，或者只取所需要的某几个 bit 位。比如，清除 1111 0000 的 bit4 和 bit5 ：

1111 0000 & 1100 0000 = 1100 0000    // 对 1111 0000 的 bit4/bit5 清0

1111 1001 & 0000 1111 = 0000 1001    // 只取 1111 1001 的低4位。与0位与可去除不需要的位，与1位与，保留所需的位

对特定位 & 1 进行运算，其实就是保留原来的值。

1.2 位或 |

真值表：Y = A + B

A	B	Y
0	0	0
0	1	1
1	0	1
1	1	1

特点：同一二进制位上，只有0和0进行或运算，其结果才为0，其余全是1。

该特点可以对某个特定位置1，比如：

0011 0000 | 0000 1111 = 0011 1111;  // 即对 0011 0011 操作数的低4位置1了

对特定位进行 | 0，则保留原值。

1.3 位取反 ~

位取反就是对操作数的二进制位按位进行取反操作，0 取反则为1，1取反则为0，如下：

~0 = 1;
~1 = 0;

~1100 = 0011;

按位取反，和非运算（!）是不一样的，非运算只有0或者1的结果。

1.4 按位异或 ^

真值表：Y = A + B

A	B	Y
0	0	0
0	1	1
1	0	1
1	1	0

特点：同一二进制位上，两个位相等则为0，否则为1。

该特点，可以对操作数的特定位进行反转操作。

1100 1111 | 1111 0000 = 0011 1111;     // 即把 1100 1111 操作数的高4位进行了反转

对特定为进行 ^ 0，则保留原值。

1.5 左移 <<

对一个操作数的二进制位进行左移 n 位操作。其中左边移出去的二进制位进行丢弃，右边空出的二进制位补0。

如对 0x05 左移 3 位：

0000 0101 << 3 = 0010 1000 = 40

左移1位相当于该操作数乘以2，左移n位，则是乘以 2 的 n 次方， (x<<n) = x*2^n。5 * (2^3 ) = 40。所以 5 左移 3 位，即 5 * (2^3 ) = 40.

1.6 右移 >>

对一个操作数的二进制位进行右移 n 位操作。其中右边移出去的丢弃，左边空出的高位是补0还是补1则要看操作数是有符号数还是无符号数。

• 无符号数右移：空出的高位补0，这种情况称为逻辑右移。
• 有符号数右移：空出的高位全部以符号位进行填充，即正数补0，负数补1。这种情况称为算数右移。

如对 5 和 -5 右移 2 位：

// 5 和 -5 的二进制展开形式分别是：
// 00000101(5) 11111101(-5)    
00000101 >> 2 = 00000001;  // 十进制就是1
11111101 >> 2 = 11111110;  // 十进制就是0

右移1位相当于该操作数除以2，右移n位，则是除以 2 的 n 次方，(x>>n) = x/2^n

2. 如何操作寄存器位

SOC中的每个寄存器基本占32bit，每个寄存器位可能占1个bit或多个bit，我们如何操作寄存器特定的1个或几个bit位，但又不能影响寄存器的其他bit呢？

可以遵循读-改-写的策略。先把整个寄存器值读出来，然后修改特定的bit位，然后再整体写回寄存器中。

2.1 对寄存器特定位清0 &

我们想要对寄存器特定的一位或几位进行清0操作，但不能影响其他bit位，可以先构造出一个合适的数（想要对哪个位清0，那么该位构造为0，其他位保持为1），然后使用这个数和寄存器原来的值进行位与操作。

比如：对一个32位的寄存器的 2~5 这几个位清0，那么就构造一个 2~5 bit都是0，其余位均为1，那么这个数就是（可以使用计算器工具去获得这个数，下文会介绍构造这个数的技巧）：0xFFFFFFC3

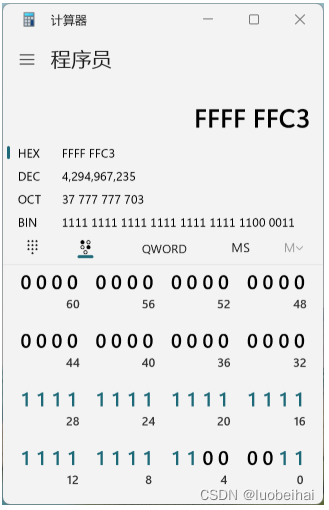
那么对寄存器 bit2~5 清0操作就是：

reg &= 0xFFFFFFC3;

2.2 对寄存器位置1 |

对特定的寄存器位置1操作而不影响其他bit，使用位或运算。同样的，我们可以构造一个合适的数，然后和这个寄存器原来的值进行位或操作。而这个合适的数构造原则就是：需要置1的位构造为1，其余为保持为0.

比如，对一个32位的寄存器的 2~5 这几个位置1，那么构造出来的数就是：0x00000060

那么对寄存器 bit2~5 清0操作就是：

reg |= 0x00000060;

2.3 对寄存器特定位取反 ^

如果我们想要吧寄存器的某些特定位，从1变为0，0变为1，也就是取反的操作，但不能影响其他bit位。同样也是可以构造一个合适的数的，然后这个数和寄存器值进行异或操作。异或要构造的数的规则，与置1的操作是一样的。

比如，一个寄存器原来的值是 0xAAAAAA0F，我想要对 bit0-bit7 进行取反操作，那么构造的这个数就是：0x000000FF

reg ^= 0x000000FF;   

最终结果是：0xAAAAAAF0，这样就可以把寄存器的bit0~bit7进行取反操作了。

3. 使用位操作构造任意二进制数

从上面的操作来看，想要对寄存器某个或某些特定位进行清0、置1、取反操作，其最重要的就是要构造一个数。根据不同的操作，构造这个数也会不同，比如清0，那么构造的数某个位为0。置1，则构造的数某个位为1，取反构造数的规则与置1是一样的。然后我们根据这个规则，通过计算器计算出来的，或者你也可以想象出来。

但是我们其实可以提供位操作，可以去构造出任意的二进制数，这比计算器或者自己想出来好得多了。

3.1 构造特定bit位为1的二进制数

我们可以使用移位操作，来获取任意bit位为1的二进制数。

比如上面的介绍的，为了让 bit2~5 位置1，我们需要构造 bit2~5 为1（其他位为0，下面不在说明）的一个二进制数，可以先这样做：

• bit2~5 一共有 5-2+1=4个bit，4个bit就是0xf

• 那么获得构造的数就是 0x0f << 2

通过上面两步，我们就可以获得任意bit位为1的二进制数了。

但是我们想要构造 bit2~5 和 bit19~20 为1的二进制数呢？这时可以先构造bit2_{5的数，以及bit19}20的数，然后使用位或操作。如下：

• bit2~5：构造的基准数为0x0f

• bit19~20：构造的基准数为 0x03

• 移位加上位或运算：(0x0f<<2) | (0x03<<19)

上面三步就可以构造这种需要叠加bit位的情况了。而且可读性比你使用计算器算出来一个最终的结果好多了。

3.2 结合位取反构造特定bit位为0的二进制数

构造一个 bit3~11 的位为0，其余均为1的数，如何操作？我们根据上面的步骤，然后加入位取反的操作即可构造出特定bit位为0的数。

比如说我们要构造bit3~9为0，其余位均为1的二进制数：

• bit3~9 一共 9-3+1=7个bit。bit3_{9为0，那么反码bit3}9为1，即这个基准数就是：0x7f
• 然后进行移位操作，0x7f<<3
• 然后进行取反操作 ，~(0x7f<<3)

这样构造出来的数，可读性好多了。

总结：

1. 如果你要构造的数大部分bit位为0，少部分是1，那么可以连续多个1左移n位得到；
2. 如果你要构造的数大部分bit位为1，少部分是0，那么在先构造该数的反码，然后再进行位取反即可；
3. 如果要构造的数，连续 1（或者0）是由多个部分组成了，可以先构造各个部分的数，然后再使用位或操作即可。

4. 寄存器操作综合应用

1）对特定bit位清0或置1

比如说，对bit3置位，前面说过，置位使用 | 运算，我们先构造 bit3 为1的数，即 1<<3，然后进行位或操作：

reg |= (a<<3);

又比如对bit20清0，那么使用 & 运算，我们先构造 bit20 为0的数，即 ~(1<<20) ，然后再进行位与操作：

reg &= ~(1<<20);

使用下面宏定义封装起来：

#define CLR_BIT(reg, n) ((reg) &= ~(1 << (n)))
#define SET_BIT(reg, n) ((reg) |= (1 << (n)))

2）对连续几个bit位清0或者置1

这是对连续的几个bit进行置位或者清零，其实和上面对一个bit置位或清零一样的。比如：

bit11~14位置1：

// 1. 先构造bit11~16位为1的数：0x3f<<11
// 2. 然后进行位或操作：reg |= (0x3f<<11)
reg |= (0x3f<<11)

bit17~23位清0：

// 1. 先构造bit17~23位为0的数，23-17+1=7个bit，那么这个数就是：~(0x7f<<17)
// 2. 然后进行位与操作：reg &= ~(0x7f<<17)
reg &= ~(0x7f<<17);

// 对连续 n~m bit为进行清0操作，使用宏定义进行封装
#define  CLR_BIT_N_TO_M(reg, n, m)     (reg &= ~((~(0U) << (m-n+1)) << n))

3）取出寄存器bit5~9的值

取出bit5_{9的值，那么就是bit5}9的值保持不变，其余位则为0，然后再右移5位，即可把bit5~9取出来。

在前面的位运算综述就介绍过，要取出特定的bit位，使用位与 & 运算。那取出 bit5~9 位的值思路如下：

• 先构造 bit5~9 为1的数：0x1f << 5
• 把 bit5~9 位保留，其余位全部清0，即位与运算：reg &= (0x1f << 5)
• 最后把得到的值，在右移 5bit，即可取出bit5~9位的值：reg >>= 5

4）对某个或连续几个特定bit位取反

前面就介绍过，对寄存器特定位取反操作，可以使用按位异或。

• 对第 n 位进行取反：

  // 1. 先构造一个第 n 位为1的数，即： 1<<n
  // 2. 然后再进行异或操作：reg ^= (1<<n)
  reg ^= (1<<n);
  
  // 使用宏定义进行封装
  #define  REVERSE_BIT(reg, n)     ((reg) ^= (1<<(n)))
  

• 对连续几个特定bit位取反

  比如说，对bit4~10取反。思路也是一样的，先构造 bit4~10 为 1 的数，然后再进行异或操作。

  // 1. 先构造一个 bit4~10 位为1的数，10-4+1=7，即一共7个bit位为1。那么这个数就是 0x7f<<4
  // 2. 然后再进行异或操作：reg ^= (0x7f<<4); 这样就可以对 bit4~10 进行取反
  reg ^= (0x7f<<4);
  
  // 对连续 n~m bit为进行按位取反操作，使用宏定义进行封装
  #define  REVERSE_BIT_N_TO_M(reg, n, m)     (reg ^= ((32U - (m-n+1)) << n))
  

5）对寄存器 bit9~17 赋值0xaa

思路（注意：整个操作过程中是不能影响到其他寄存器位的。）：

• 先将 bit9~17 位清0
• 然后再把0xaa设置到 bit9~17。

那么具体操作如下：

// 1. 构造bit9~17位为0的数，17-9+1=9，即一共9个bit位为1,。那么这个数就是：~(0x1ff<<9)
// 2. bit9~17位清0， reg &= ~(0x1ff<<9)
// 3. 构造 bit9~17位的数为 0xaa，即：0xaa<<9
// 4. 最后再进行位或操作：reg |= (0xaa<<9); 即可把 0xaa 写入到 bit9~17

// C语言表示就是：
reg &= ~(0x1ff<<9);   // 先对bit9~17清0
reg |= (0xaa<<9);     // 再对bit9~17设置为0xaa