目录
第 4 章 频率域(The Frequency Domain)
4.1 频谱分析(Spectral Analysis)
4.2 物理单位(Physics units)
4.3 笛卡尔坐标形式与极坐标形式对比
4.4 频谱分析的复数形式
4.5 复数值Fourier系数
4.6 复数值的和三角的Fourier系数之间的关系
4.7 2维或多维离散Fourier变换
4.8 DFT的Matlab实现
4.9 重新审视Parseval定理
第 4 章 频率域(The Frequency Domain)
4.1 频谱分析(Spectral Analysis)
上一章介绍了如何对离散数据进行Fourier分析。 为了推导出三角函数Fourier级数模型的各种Fourier系数的公式,我们采用了“向量化”过程,其中要建模的离散函数的值被视为 D 维向量的坐标。在从图 4.1 A 到 4.1 B 的过渡中,针对 D =3 的情况说明了此向量化过程的具体示例(来自练习 4.1)。信息论创始人Claude Shannon将此过程描述为,将定义在简单空间(二维平面)中的复杂对象(波形)转换为极其复杂的 N维空间中的简单对象(点)。在第 3 章中,我们了解到这个空间也由一组三角向量构成,这些三角向量是通过对正弦波和余弦波的谐波级数进行采样而形成的。这些新的基向量相互正交,它们形成一个新的参考坐标系,如图 4.1. C 所示,它相对于用于绘制图 4.1 B 中的数据向量的原始参考系旋转。Fourier分析随后被认为是将数据向量投影到三角基向量上以生成模型的Fourier系数的行为。因此,整个过程是从不同的角度制定问题的示例,以便深入了解问题的本质并简化解决方案的计算。
为了显示和解释Fourier分析的结果,常对Fourier系数的D维向量“去向量化(e-vectorized)”处理,以便显示为新的离散函数,如图 4.1 C 到 4.1 D 的过渡所示。注意图 4.1 D 中的一对图有一个共同的 𝖷 轴,它是谐波数,𝖸 轴显示余弦(包括常数项)和正弦Fourier系数的大小。 由于谐波数(harmonic number)与模型中各种三角函数的振荡频率(frequency)成正比,图 4.1 D 显然是模型中存在的频率分量的数量的图形显示。类比玻璃棱镜(prism)对光产生的效果,这样的图形称为原始离散数据函数的频谱(frequency spectrum)。
虽然Fourier分析的计算过程遵循图4 A→B→C→D所示的阶段序列,但中间阶段(B,C)对于理解空间/时间域之间的关系不是必需的(图4A) 和频域(图 4D)。前向离散Fourier变换(DFT)将离散函数 𝗒(𝗍) 转换到频域/谱域(4A→4D),逆DFT将谱转换回时域/空间域(4 D→4 A)。这两个域(即时域和频域)是查看相同数据的互补方式,因此,Fourier分析不会获得新信息,只会获得新视角。

-----------------------------图 4.1 两种域——时域和频域-----------------------
4.2 物理单位(Physics units)
如果离散函数 𝗒(𝗑) 所地的定义的区间的长度为L ,且这个区间被均分成 D 个子区间,则在空间/时间域中水平间隔大小Δx 是
“=空间域/时间域中的分辨率”-------------------------------------------------[4.1]
样本间距离的倒数(inverse)称为采样频率或采样率 R ,因此, 。此外,相应Fourier级数的第一次(基础的)谐波分量对应频率
(译注:即长度看成一个周期)。例如,假如 L = 2米,则基础分量( k = 1)对应频率为 1/2 个周期/米(译注:基频率,一个周期对应2米,1米即0.5个周期)。则第二次谐波( k = 2) 应当是2/2 个周期/米(译注:第二次谐波频率为基波的2倍,快了一倍,相同时间跑完1个周期),第三次谐波( k = 3) 应当是3/2 个周期/米(译注:频率变为基频率的1.5倍了,相同时间跑完1.5个周期了),因此,第 k 次谐波应当具有频率
周期/米。因此,频率域中各点之间的水平间隔 Δf 是
“=频率域中的分辨率”----------------------------------------------------------[4.2]
因为Fourier系数的总数等于 D (数据点数),且因为这些系数成对出现(正弦系数项和余弦系数项),所以,所求的离散谐波数是 N = D/2(当D是偶数)或 N = (D - 1)/2(当D是奇数)。因此,最高次谐波具有频率 。因为频谱在频率区间 0 到
之间延伸,值
称为函数 𝗒(𝗑) 的带宽(bandwidth),
“=频谱带宽”------------------------------------------------------------------------[4.3]
这些结论可以组合起来(对于D为偶数的情况)以产生另外的有用公式:
“采样率 = 2×带宽”-----------------------------------[4.4]
D = 2WL “数据点数 = 2×带宽×区间长度”---------------------------[4.5]
在为实验数据指定傅立叶级数模型时,频率的物理单位通常优先于谐波数。 回想一下,一般的Fourier级数之前给出为
-------------[3.34],
当我们使用物理频率 作为k阶谐波频率,则模型成了
------[4.6]
鉴于上述定义,我们有必要的词汇来构建这样的问题:“如果我们以相同的速率采集更多样本会怎样?” 这种情况如图 4.2 所示。等式 [4.4] 表明,由于在这种情况下速率 R 是固定的,因此频谱的带宽 W 也将是固定的。

-----------------------------图 4.2 改变观察区间长度的效果---------------------
因为 W 是固定的,等式 [4.5] 表明增加数据点数量的唯一方法是延长观察区间 L 。这意味着,根据等式 [4.2],频域中各点之间的间隔 1/L 必须减小。换句话说,在固定采样率下增加样本数量的效果是在不改变其带宽的情况下增加被测频谱的频率分辨率。
相反,我们应该问:“如果我们以更快的速率采样相同的间隔会发生什么?” 如图 4.3 所示。从上面的方程组中,我们可以得出结论,在固定时间内提高采样率的效果是在不改变其频率分辨率的情况下增加被测频谱的带宽。

-----------------------------图 4.3 改变采样频率的效果-----------------------
4.3 笛卡尔坐标形式与极坐标形式对比
在第 2 章中,我们观察到余弦波与同频正弦波之和等于同频移相余弦波。也就是说,如果函数以笛卡尔形式写为 v(t) = A cos( t ) + B sin( t ),那么它也可以以极坐标形式写为 v(t) = C cos (t - Φ)。将此结果应用于当前情况,我们可以写出方程 [4.6] 的极坐标形式为
---------[4.7]
其中,
...........幅度(magnitude)
...............相位(phase) --------------------------------------------------[4.8]
在Fourier级数的这种极坐标形式中,通过分别绘制各种频率分量的幅度 m 和这些分量的相位Φ 以图形方式显示频谱。一个例子如图 4.4 所示,在电气工程中,这样的图形通常被称为波德图(Bode plot)。请注意,幅度始终为正,相位被限制在区间 (0 - 2π)内。

-----------------------------图 4.4 频率的两种形式:笛卡尔和极坐标---------------------------------
4.4 频谱分析的复数形式
等式[4.6]中Fourier级数的形式,促使我们使用复数来表示频谱,因为级数中三角函数项成对出现,每个谐波显示为余弦波和正弦波的加权和。在第 2 章中,我们学习了如何将这种组合有效地描述为绘制在复平面上的相量。在代数上,这些相量等同于复数,其中数的“实”部分是余弦函数的权重,数的“虚”部分是正弦函数的权重(译重,权重(weight),我们姑且把它当成一个衡量其级数项相对重要性的乘法因子)。 为了采用这种方法,我们使用练习 2.3 中证明的Euler公式(译注:即反映指数函数与三角函数关系的公式 , 因为此函数为周期函数,只写 θ 即可,也可写成 nθ)。
---------------------------------------------[4.9]
[译注,在 Euler公式中,令解度为 -θ,则有 ,将两式分别相加相减即可求出cos(θ)和sin(θ)的表达式。]
在开区间(0,2π)上重写离散函数的Fourier级数为
---------------------------------------------------------------------------------------------------------[4.10]
假如我们收集具有公共指数因子的项,则等式成为
---------------------------------------------------------------------------------------------------------[4.11]
现在,我们定义通用的Fourier系数的复数形式 为
----------------------------------------------------------------------------------------[4.12]
则等式[4.7]的Fourier级数就转化成了
--------------------------------------------------------------[4.13]
Fourier级数的这种极其紧凑的形式在该主题的教科书作者中非常流行。请注意,用复数指数代替三角函数需要负谐波。 其原因在Euler方程 [4.9] 中很明显:即使是简单的余弦函数也是两个复数指数的和,一个具有正角,另一个具有负角。 图 4.5 显示了笛卡尔和极坐标形式的余弦波形的复值Fourier频谱的图形表示。

-----------------------------图 4.5 余弦波的复值Fourier频谱-----------------------------------------------------
负频率的含义最容易理解为反向旋转相量(参见练习 2.3),其中实部指向相同方向(因此增强)但虚部指向相反方向(因此抵消)。 这些成对相量的旋转速率是余弦函数的频率。 当两个相量反向旋转时,它们之和的长度扫出一个余弦波形。
一个潜在的混淆来源是用于显示实值Fourier频谱的频率轴(图 4.4)与用于显示复值频谱的频率轴(图 4.5)具有不同的含义。前者是指三角基函数的频率,而后者是指复指数函数的频率。 如果作者未能明确地说明使用哪种类型的基函数来计算Fourier频谱,则读者需根据上下文背景来自行决定。 如果频率轴包含负值,这很容易做到,因为只有复指数使用负频率;按照惯例,三角频率总是正的。 然而,如果只显示复值频谱的正半部分,就会出现潜在的混淆。当光谱以极坐标形式显示时,这种情况并不少见,因为对于实值数据,幅度谱总是关于 𝗒 轴对称,因此光谱的负半部分是多余的,并且经常被作者或出版商压制。
4.5 复数值Fourier系数
根据具有复系数的复数指数重写Fourier级数模型后,应该可以重复第 3 章中使用的三角模型分析路线,从而验证等式中的公式。[4.12] 将产生这些复数值Fourier系数的数值。 在这里验证 D = 3 的情况然后将结果推广到任何 D 就足够了。因此,我们采用与第 3.F(译注:3.6节) 节中相同的方法,并在每个 𝖷 值处我们有可用采样点时计算Fourier级数[4.13]。(译注:以下假设在开区间(0,2π)上采样)
.............@ X = 0
.............@ X = L/3
.............@ X = 2L/3
为了解这个方程组,我们首先写成矩阵形式 v = Q.h 如下
--------------------[4.16]
当按这种方式书写时,矩阵Q的列应当考虑成列向量 ,
,和
,这是由采样的指数函数创造的,采样指数函数组成了我们的Fourier模型的基。用h 表示复数的Fourier系数,我们也可以使用先前创立的对采样的三角向量使用的紧凑记法,写为(用向下的箭头表示列向量)
-------------------------------------------------------------[4.17]
此等式意味着,向量 v 是基向量的加权和
。--------------------------------------------------[4.18]
对于在区间 2π上 D 采样的通用情况,其逆DFT关系 v = Q.h 是
(IDFT)--------------------------------------------------------------------[4.19]
其中,通用基向量由
,其中,
给出。------------------------------------------------------------------- [4.20]
注意,当k是负数时,也适用复数基向量的描述,因为的k符号也包含在指数函数的指数中。
这一发展表明,如果我们遵循第 3 章中基函数是采样三角函数时使用的相同推理路线,那么对于由采样复数指数构成的基函数,也会出现类似的情况。这种发展是可能的,因为当矩阵和向量的元素是复数或只是实数时,矩阵代数定律同样适用。 因此,从代数的角度来看,即使很难在几何上可视化这些新的复数值基函数,方程 [4.18] 也是有意义的。
为了确定这种模型的Fourier系数,我们需要前向DFT关系 。我们之前使用的求逆矩阵的方法是将数据向量 v 依次投影到每个基向量上,形成一个内积。这是可行的,因为基向量是正交的。留作练习来验证基向量集 Q 是否相互正交,并且都具有相同的长度,并且都等于
。 这些观察结果表明重新排序和缩放等式 [4.17] 中的项。得到反DFT公式
----------------------------------------------[4.21]
通过用逆矩阵(通过转置和共轭变换矩阵获得)在两边预乘来求解 f 的等式 [4.21] 得到直接 DFT公式
---------------------------------------------------[4.22]
星号表示向量的复数共轭,它是通过取每个单独分量的共轭而获到的。这最后两个等式程是三角基函数[3.38]和[3.39]的类比。 类比于等式[3.30, 3.31]的复数值Fourier系数的显式公式是
------------------------------------------------------------------------------------------------------------------------[4.23]
学生此时可能想知道,为什么Fourier分析这个主题已经足够复杂了,因为引入了复数值基函数和复数值Fourier系数而变得更加复杂。主要动机在于 DFT 等式 [4.22] 无论数据向量中的测量值是复数值还是实数值,都同样适用。换句话说,通过允许复数值数据,Fourier分析的范围通过承认那些具有两个属性而不是只有一个属性的物理变量而大大扩展。 例如,力、速度(velocity)、动量(momentum)、电磁波(electromagnetic waves)和无数其他本质上是二维的物理参数(即大小和方向),可以使用与分析本质上是1维的(例如电压、光强度、质量等)“实”函数完全相同的程序来进行分析。由于Fourier分析的整个主题可以像复数值函数一样容易地展开,实数值函数被视为一般结果涵盖的特例,这是大多数教科书作者和计算机程序员所青睐的方法。
4.6 复数值的和三角的Fourier系数之间的关系
考虑到许多作者倾向于使用复数形式的Fourier叶分析,以及初学者希望更接近三角基函数的“现实(reality)”,能够轻松地将这两种方法联系起来就变得很重要。为此,我们首先用三角函数展开基向量 Q。 例如,对于 D = 3 的情况
------------------------------------------------------------------------------[4.24]
也就是说,新的基向量Q是采样余弦向量C和i乘以采样正弦向量S的和。换句话说,Q的实部等于C,Q的虚部等于S。 实际上,我们已经概括了第 2 章的思想(其中复数被视为相量以探索它们的几何性质),因此复向量被视为实向量和虚向量之和。另请注意,负频率的基向量是
-----------------------------------------------------------------------------------------------[4.25]
换句话说,正负频率的基向量是互为复数共轭的。
将这些表达式代入等式[4.22]将根据三角系数产生复数Fourier系数的向量
-------------------------[4.26]
这些矩阵乘法所隐含的各种内积可从等式 [3.21] 和 [3.22]中所知。 因此,利用这些信息,我们拥有
------------------------------------------------[4.27]
将这个结论推广以包括任何三角Fourier系数,复数系数是
-----------------------------------------------------------------------------------[4.28]
该结果与等式[4.12]中Fourier系数的原始定义相匹配。这是对前面的开发是否正确的有用验证。注意, 和
互为复数共轭。这意味着实数值离散函数的频谱具有一种特别对称性——Hermite对称或共轭对称,按下列关系定义
(偶对称)
(奇对称) ---------------------------------------------------------[4.29]
已知复系数,则三角系数是
-----------------------------------------------------------------------------------------------------------------------[4.30]
这与等式[4.12]中定义的原始定义一致。
上面以笛卡尔形式描述了三角函数和复数Fourier系数,但它们也可以用极坐标形式(即幅度、相位)表示。根据等式 [4.28] 复系数的大小是
------------------------------------------------------------------[4.31]
请注意,两个模型中的常数项相同,但是将此结果与等式[4.8]进行比较,我们看到其他复数系数的大小恰好是三角系数极坐标大小的一半。即,
----------------------------------------------------------------------------[4.32]
考察这个结论的一种方法是,当余弦函数用一对复指数表示时,它的振幅被分成两半。幅度的一半出现在频谱的正频率部分,另一半出现在频谱的负频率部分。至于相位,两种Fourier系数的相位角由下式给出
--------------------------------------------------------------------------------[4.33]
图 4.6 以笛卡尔(矩形)形式和极坐标形式显示了比较三角和复数Fourier频谱的假设(hypothetical)示例。注意左下方面板中的Hermite对称性。右下面板也存在类似的对称性,因为频谱的幅度部分具有偶对称性,而相位谱具有奇对称性。
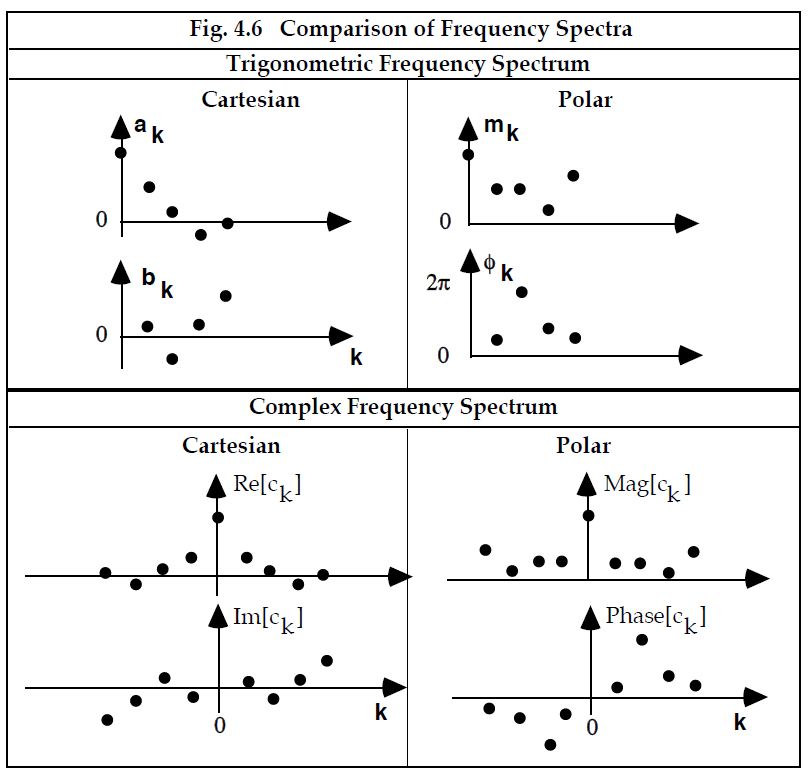
-------------------------------------------------图4.6 频率谱对比----------------------------------------------------
4.7 2维或多维离散Fourier变换
将等式[4.14]中给出的一维Fourier级数推广到在 L×L 平方上采样的2维函数世界得到
------------------[4.34]
请注意,括号内的表达式是一维Fourier级数,其系数 是通过在数据矩阵的行上计算的一系列一维 DFT 得到的。结果是Fourier系数的二维矩阵,现在成为要对列进行一系列 DFT 计算的“数据”。因此,二维 DFT归结为一系列两个一维 DFT,其中第一个是为原始计算的数据,第二个根据第一个的结果计算。这种方法可以很容易地推广到 3 维体积数据等等到 N 维空间。
4.8 DFT的Matlab实现
根据Matlab文档,FFX(𝗑)返回向量 𝗑 的离散Fourier变换。对于长度为D的输入向量 𝗑 ,DFT 是一个长度为N的向量f , 其元素为
-----------------[4.35]
(译注:exp记法以Euler数e为底的指数表达式,扩号中的部分为指数部分。)
请注意,此公式中使用 (n - 1) 意味着 MATLAB 假设采样时间从 0 开始,间隔长度为 2pi(译注:2π)。这意味着用户负责跟踪与实际采样时间相关的相移和物理频率。(我们将在第 6 章处理相移(phase shifts))。家庭作业练习中使用的另一种方法是使用真实采样时间来计算采样基函数。还要注意等式[4.35]的定义。不包括使变换矩阵正交所需的归一化常数 1/D。此外,根据文档,Fourier级数中DFT与Fourier系数a和b之间的关系
----------------------------------------------------------------------------------------------------------[4.36]
是
------------------------------------------[4.37]
其中,𝗑 是一个长度为 D 的向量,其包含连续函数在时刻t以跨度Δt = L/D间隔采样的离散值。等式 [4.36] 和我们的 [3.34] 之间的差异表明定义Fourier级数的不同约定。 我们选择在变换矩阵中包含样本点数 D 以获得正交矩阵,因此因子 D 包含在我们的Fourier系数中。然而,Matlab 将D 从变换矩阵中排除,因此该因子必须明确包含在等式[4.36]的Fourier级数中。这些差异对使用 Parseval 定理的方差统计(bookkeeping)有影响。
另请注意,FFT 返回的Fourier系数的排序对应于谐波数 0 到 D - 1,而不是 - D /2 到 D /2。 这里有两个问题需要解决。首先,似乎 Matlab 使用的谐波数都是正的,而不是一半正一半负。事实上,采样基函数的周期性导致大于 D/2 的正谐波数(逆时针旋转)等于负谐波数(顺时针旋转)。 图 4.7 以图形方式显示了这一事实。 其次,Matlab 首先报告频率轴正半部分的傅里叶系数,然后是负半部分。 为了颠倒这个顺序,Matlab 提供了一个函数 FFTSHIFT(FFT(x))来交换Fourier向量的两半。 这将零频率放在Fourier矢量的中间,便于绘制频谱。但是,在使用Matlab函数IFFT执行逆 DFT 之前,使用 IFFTSHIFT 将Fourier向量返回到标准格式非常重要。

------------------------------------------------图4.7 复数基函数---------------------------------------------------
4.9 重新审视Parseval定理
Parseval 定理在第 3 章中被表述为
------------[3.45]
用等式中给出的复值Fourier系数替换 [3.45] 中的三角系数。 [4.30] 结果是
-----------------------------------------------------------------------------------------[4.38]
在Matlab中,这个结果写为v*v’/D = h*h’ ,其中,v是数据向量,h是对复指数基函数取得的Fourier系数向量。
内容来源:
<< Fourier Analysis for Beginners>> Larry N. Thibos