博主主页:Yu·仙笙
专栏地址:洛谷千题详解
目录
题目描述
输入格式
输出格式
输入输出样例
解析:
C++源码:
Java源码:
--------------------------------------------------------------------------------------------------------------------------------
 --------------------------------------------------------------------------------------------------------------------------------
--------------------------------------------------------------------------------------------------------------------------------
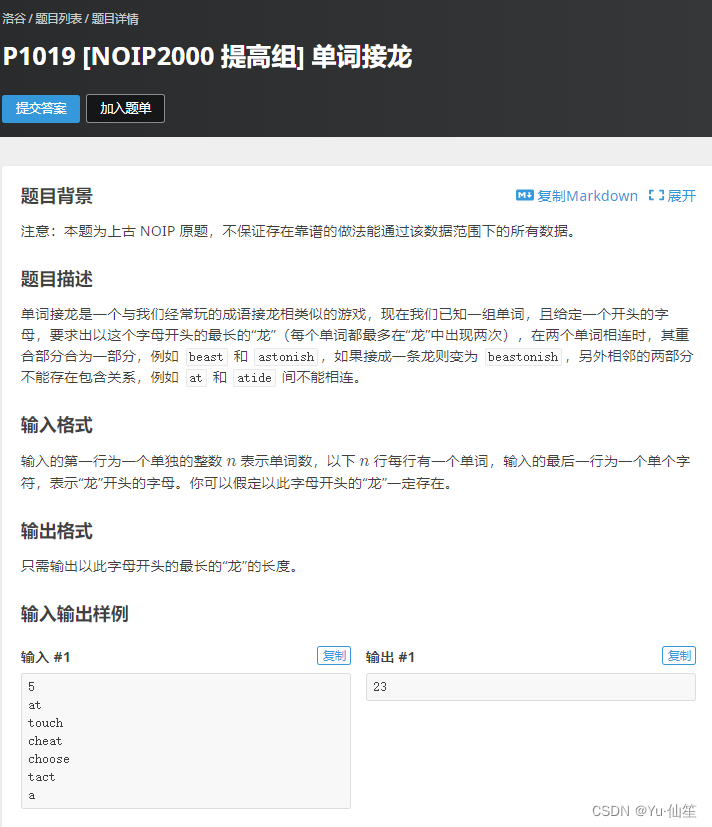
题目描述
单词接龙是一个与我们经常玩的成语接龙相类似的游戏,现在我们已知一组单词,且给定一个开头的字母,要求出以这个字母开头的最长的“龙”(每个单词都最多在“龙”中出现两次),在两个单词相连时,其重合部分合为一部分,例如
beast和astonish,如果接成一条龙则变为beastonish,另外相邻的两部分不能存在包含关系,例如at和atide间不能相连。
--------------------------------------------------------------------------------------------------------------------------------
输入格式
输入的第一行为一个单独的整数 n 表示单词数,以下 n 行每行有一个单词,输入的最后一行为一个单个字符,表示“龙”开头的字母。你可以假定以此字母开头的“龙”一定存在。
--------------------------------------------------------------------------------------------------------------------------------
输出格式
只需输出以此字母开头的最长的“龙”的长度。
--------------------------------------------------------------------------------------------------------------------------------
输入输出样例
输入 #1
5 at touch cheat choose tact a输出 #1
--------------------------------------------------------------------------------------------------------------------------------
解析:
谨以此题解纪念我的洛谷橙名,我会继续努力。
基本思路是搜索。
处理的难点在于对重叠部分的处理。
单词的使用次数很好判断,开一个数组即可,和正常向dfs的vis数组差不多。
但对于重叠部分的处理,我想细说一下。
因为连接起来的单词要最长,所以对比是选择从上一个单词的末尾与当前单词的开头进行比对,如果发现不符那就不能匹配。
这里我借鉴了一位大神的思路,使用一个check函数,用来比较两个串s和m的长度为k的接口能不能匹配。
判断方式有两种,第一种就是我用的这样按字符比较,如果发现某处不匹配立即返回false。还有一个方法是用string里面的substr,我就不展开了,有兴趣的同学可以试一下。
我们假设接口长度为k,串s的长度为lens,然后我们从0到k枚举,判断s[lens-k+i]是不是等于m[i]。
这个式子怎么来的呢?接口前面的串是s,后面的串是m,那么很显然,s串的接口最开始应该是lens-k处,然后在后面加上一个枚举的i就可以保证扫描到所有接口字符(我们的i是从0开始枚举的)。
还有一些细节问题。 如果我们在接龙的时候发现我们现在要接的龙还不如之前某一次接过的长,那么这个接龙方案肯定不是最优的,所以要舍去,这个正确性是显然的。
(想一下深搜时的遍历过程,这句话便不难理解)
使用我这个方法,可能有一个奇怪的想法有同学没想到,那就是在进行拼接操作时,要注意使用给定的串的副本(即复制一份原来的串)进行拼接处理。
这是因为,如果你把原串改变了,而且这个串还不是最优的,那就完了,回溯不回去了。
具体到操作上,首先,我们从1到n枚举每个短字符串,如果它已经被用了两次则continue,然后我们求出当前短串的长度,从1到这个长度枚举,枚举的是接口的长度(自然是接口越短融合串越长嘛) 然后执行拼接操作,记录一下最大长度,再加上回溯就好了。
拼接操作和check函数很像,具体到代码上大家就能看明白了。
--------------------------------------------------------------------------------------------------------------------------------
C++源码:
#include<cstdio>
#include<iostream>
#include<string>
#include<cmath>
using namespace std;
int n;//单词数
string tr[30];//存储字符串
int yc[30][30];//两个字母的最小重叠部分
int vis[30];//判断单词使用频率.
int mt(int x, int y){//mt函数,返回x单词后连接一个y单词的最小重叠部分
bool pp=true;
int ky=0;
for(int k=tr[x].size()-1;k>=0;k--){//从x单词尾部向前看看最小重叠部分是从哪里开始的,以为因为是倒着来,所以保证是最小的
for(int kx=k;kx<tr[x].size();kx++){/
if(tr[x][kx]!=tr[y][ky++]){
pp=false;
break;
}
}
if(pp==true){//如果说当前以k为开头的前一个单词后缀 ,是后面单词的前缀,就马上返回重叠部分。(tr[x].size()-k是找出来的规律)
return tr[x].size()-k; }
ky=0;
pp=true;//不行就继续
}
return 0;
}//可能这里有点难理解。可以手动模拟一下
char ch;//开头字母
int ans=-1;//答案
int an=0;//每次搜到的当前最长串
void dfs(int p){//p为尾部单词编号(p的后缀就是“龙”的后缀,因为p已经连接到”龙“后面了)
bool jx=false;
for(int j=1;j<=n;j++){
if(vis[j]>=2) continue;//使用了两次就跳过
if(yc[p][j]==0) continue;//两单词之间没有重合部分就跳过
if(yc[p][j]==tr[p].size() || yc[p][j]==tr[j].size()) continue;//两者存在包含关系就跳过
an+=tr[j].size()-yc[p][j];//两单词合并再减去最小重合部分
vis[j]++;//使用了一次
jx=true;//标记一下当前已经成功匹配到一个可以连接的部分
dfs(j); //接上去
an-=tr[j].size()-yc[p][j];//回溯,就要再减回去那一部分长度
vis[j]--;//回溯,使用--
}
if(jx==false){//jx==false说明不能再找到任何一个单词可以相连了
ans=max(ans,an);//更新ans
}
return;
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++)
cin>>tr[i];
cin>>ch;
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
yc[i][j]=mt(i,j);
}
}//预处理yc数组。yc[i][j]就表示,i单词后连接一个j单词的最小重叠部分
//比如 i表示at,j表示att. yc[i][j]就为2 但是yc[j][i]就为0.
//预处理是一个关键
for(int i=1;i<=n;i++){//从头到尾看一下有没有以指定开头字母为开头的单词
if(tr[i][0]==ch){//如果有,就以当前单词为基准进行搜索。
vis[i]++;//使用过一次
an=tr[i].size();//更新当前串长度
dfs(i);//接上
vis[i]=0;//消除影响
}
}
printf("%d",ans);
return 0;
}#include <iostream>
#include <cstdio>
#include <cstring>
#include <string>
#define maxn 100
using namespace std;
int n;
int ans = 0;
string word[maxn];//字符串数组,用来存储单词
string beginn;//用来存储开头字符
int used[maxn];//这个就是用来记录dfs时候每一个单词被使用了几次的数组
bool check(string s,string m,int k){//重点一,check函数判断接口可行性,k代表接口长度,以下同
int lens = s.length();
for (int i=0;i<k;i++){
if(s[lens-k+i]!=m[i])//我讲过了
return false;
}
return true;
}
void add(string &s,string m,int k){//拼接操作,因为要把m接到s上,所以对于s串不可以传参,因为我们要试图改变这个串
int lenm = m.length();
for (int i=k;i<lenm;i++)
s+=m[i];//C++字符串类型特性操作,支持+=符号直接拼接
}
void dfs(string now){//这只是一个看似平淡无奇的dfs
int x = now.length();
ans = max(ans,x);//每次拼接之后更新一下答案
for (int i=1;i<=n;i++){
if (used[i]>=2)//如果有一个单词用完了,那这个单词就不能选了
continue;
int maxk = word[i].length();
for (int j=1;j<=maxk;j++){//枚举接口长度
if (check(now,word[i],j)){
string temp = now;//重点二,使用字符串副本进行拼接
add(temp,word[i],j);
if (temp==now)//拼完之后如果发现长度没增加,也就是和原串一样,那这次拼接没有意义,剪掉
continue;
used[i]++;
dfs(temp);
used[i]--;//这只是一个看似平淡无奇的回溯
}
}
}
}
int main(){
cin >> n;
for (int i=1;i<=n;i++)
cin >> word[i];
cin >> beginn;
dfs(beginn);
cout << ans << endl;
return 0;
}--------------------------------------------------------------------------------------------------------------------------------
Java源码:
import java.util.Scanner;
public class P1019 {
// 要点:
// 1.单词拼接一定要相同的部分:能连接
// 2.在保证能连接的情况下,保证连接长度最长
// 3.不能存在包含关系
static String []a=new String[30];//存储单词
static int []use_times=new int[30];//使用次数
static int p=0;
static int n=0,ans=0;//N为单词数,ans是长度
//用于查找两字符串是否是包含关系,或者相同的有多少个单词
public static int find(int index,int y) {//y为当前匹配的单词,index为龙当前的最后一个单词
for(int i=a[index].length()-1;i>=1;i--) {//查找龙的最后一个单词从尾部向前搜索和匹配单词的开头相同的位置
if(a[index].substring(i, i+1).equals(a[y].substring(0,1))) {
int k=0;//设立临时值,用于单词匹配数
for(int j=i+1;j<a[index].length();j++) {//如果龙的最后一个匹配,则直接退出,保证单词连接最长。
k++;
if(!a[index].substring(j,j+1).equals(a[y].substring(k,k+1))) {
//如果某个字母不相同,表示两个字符串没有公共部分。无法连接在一起
return 0;
}
}
return a[y].length()-k-1;//能到这,最起码都是第一个匹配成功
}
}
return 0;
}
public static void dfs(int x) {//x为当前位置
for(int i=1;i<=n;i++) {
if(use_times[i]<2&&find(x,i)>0) {//单词不能用两次,并且不能包含:表示连接
use_times[i]++;//使用次数加一
ans+=find(x,i);//加上新单词长度
dfs(i);//接着这个单词搜索
use_times[i]--;//回溯
ans-=find(x,i);
}
}
if(ans>p)
p=ans;
}
public static void main(String[] args) {
Scanner cin =new Scanner(System.in);
n=cin.nextInt();//单词数
int maxn=0;
for(int i=1;i<=n;i++) {//存储单词
a[i]=cin.next();
}
String b=cin.next();//龙的开头
for(int i = 1; i <= n; i++)
{
if(a[i].substring(0,1).equals(b))//查找首字母为龙的开头的单词
{
ans = a[i].length();//先加上首单词的长度
use_times[i]++;//首单词用过了
dfs(i);//以第i个单词为开头,尝试计算长度
use_times[i]--;//回溯
if(p > maxn)//求最大
{
maxn = p;
}
}
}
System.out.println(maxn);
cin.close();
}
}
--------------------------------------------------------------------------------------------------------------------------------





![[附源码]JAVA毕业设计货币博物馆展品管理系统(系统+LW)](https://img-blog.csdnimg.cn/3c12480b2ac847488db944a0d8a989b2.png)