1. (简答题)

1.（教材3.4）（a）假设某一个算法的时间代价为

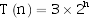
，对于输入规模n，在某台计算机上实现并完成该算法的时间为t秒。现在另有一台计算机，运行速度为第一台的64倍，那么t秒内新机器上能完成的输入规模为多大？

2.（教材3.12）

写出下列程序段平均情况下时间代价的Θ表示式。假设所有变量类型都为int：

(f)

   sum = 0;

    for (i = 1; i <= n; i*=2)

        for (j = 1; j <= n; j++)

            sum ++;

(g)假设数组A中含有n个元素，函数Random花的时间是常数值，sort需要执行nlogn步。

    for (i = 0; i < n; i++) {

        for (j = 0; j < n; j++)

            A[i] = Random(n);

        sort(A, n);

    }

(h)假设数组A中元素为从0到n-1的任意一个排列。

    sum3 = 0;

    for (i = 0; i < n; i++)

        for (j = 0; A[j] != i; j++)

            sum3 ++;

(i)

    sum = 0;

    if (EVEN(n))

        for (i = 0; i < n; i++)

            sum ++;

    else

        sum = sum +n;

3. 算法分析题，阅读以下代码：

int a[100];

Fun(int a[], int n)

{

    for(int i=1; i<=n; ++i)

    {

        cin>>a[i];

    }

    int K=1;

    for(int i=1; i<=n; ++i)

    {

        if(i > 1 && a[i] < a[i - 1])

        K = i;

        while (K < n && a[i] >= a[K +1])

            ++ K;

        cout<< K;

    }

}

若输入的a数组是一个严格单调递增的数列，分析此程序的时间复杂度。

注意：课后作业必须在作业本上完成，需要有完整的计算过程。在截止时间之前，在系统提交答案照片。

作业本统一交给课代表。