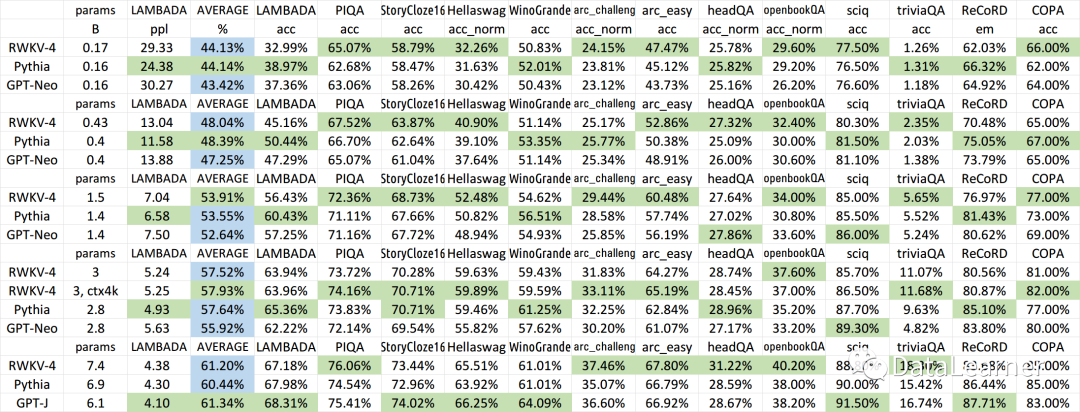
只是一个记录
8层12头512维度的 GPT 模型,使用它来记忆 10000 条 512长度 的无序序列,vocab_size 为100。
模型要自回归生成这些序列,不可能依赖局部推理,必须依赖全局视野,即记住前面的序列。
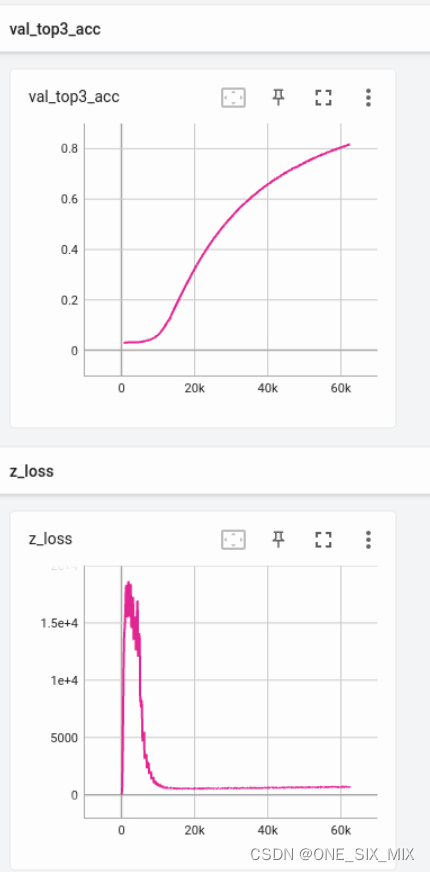
然后统计 最后一个norm层前的 latent 的 均方根值。然后发现,这个值会在训练初期迅速飙升到1e4 - 1e6 的域,非常巨大,如果使用半精度训练,会直接撑爆然后变成nan,只能使用float32值域训练。
一开始,我以为这模型又完蛋了,但后面让他继续训练,发现它居然在缓缓下降,当下降到 1e2 - 1e3 的以内的域时,模型基本记忆正确率已经 90%以上了。
在自然语言序列的训练中,这个值从来没有这么大过,最大也就500以内。
然后检查了这么巨大的值的来源,发现来源有两个,一个是注意力计算的第二个矩阵乘法。
out = v @ a
一个是 注意力计算的最后一个层。
但是神奇的是,这个注意层的各个权重是正常的,即权重的标准差均在1以内。(不过这也是能收敛的基础,权重不正常那基本不可能收敛)
下面的 z_loss 就是潜变量的 均方根
还是老问题,全局能力强的,局部能力就差。局部能力强的,全局能力就差。
写的在全局性能上很好的,在无序序列的模型收敛很快,在自然语言上被普通gpt秒成渣(指验证集分数提升慢,最终分数也差一点)
而普通的gpt模型,在自然语言上效果很好,但在记忆无序序列上,收敛速度极慢。
不知道有什么办法能结合他们优点,搞一个全局性能和局部性能兼优的模型