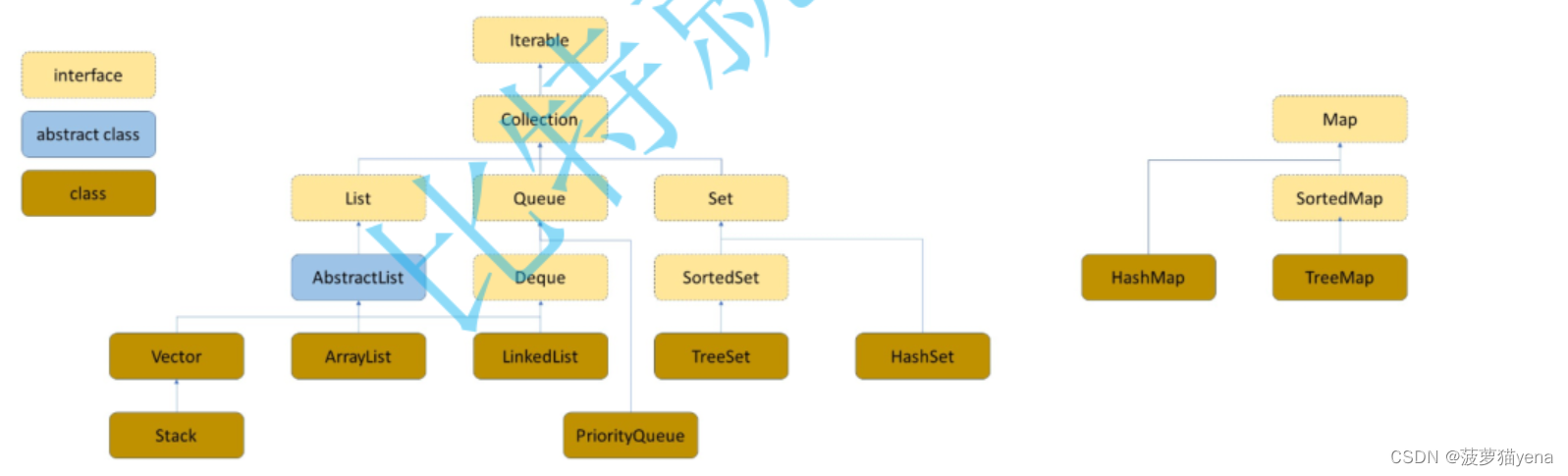
集合、列表和数组

1.集合：

集合一般被定义为由一个或多个确定的元素所构成的整体。通俗来讲，集合就是将一组事物组合在一起。你可以将商店里的所有物品当成一个集合。

特点：

1. 集合里的元素没有顺序
2. 集合里的元素类型不一定相同

2.列表（又称线性列表）：

列表是一种数据项构成的有限序列，即按照一定的线性顺序，排列而成的数据项的集合。列表的概念是在集合的特征上形成的，它具有顺序，且长度是可变的。列表可以是一张购物清单。

特点：

1. 列表的长度是可变的
2. 列表中不存在索引这个概念

3.数组 

数组是列表的实现方式之一，它具有列表的特征，同时也具有自己的一些特征，数组会用一些名为 索引 的数字来标识每项数据在数组中的位置，且在大多数编程语言中，索引是从 0 算起的

 特点：

1. 数组的长度是可变的
2. 数组中有索引这个概念

 

 数组的操作

 LeetCode算法题：

var pivotIndex = function(nums) {
    // 先循环求出数组总和当作数组右边的和
    let rightSum = 0
    for(let item of nums){
        rightSum += item
    }
    let leftSum = 0
    for([i,item] of nums.entries()){
        // 右边的和减去当前第i个元素成为新的右边的和
        rightSum = rightSum - item 
        // 左边的和 是否等于 右边的和
        if(leftSum == rightSum){
            // 返回当前下标
            return i
        }
        // 累加左边的和
        leftSum = leftSum +item
    }
    // 找不到返回 -1
    return -1
};

 不合格的算法 时间复杂度为 O(N) 

var searchInsert = function(nums, target) {
    for(let [i,item] of nums.entries()){
        if(target !== item){
          if(item>=target){
             return i
          }else{
            if(i==nums.length-1){
                return i+1
            }
          }
        }
    }
};

合格的算法 时间复杂度为  O(log N) 

二分查找

var searchInsert = function(nums, target) {
    let left = 0 ,right = nums.length-1
    while(left<=right){
       let mid = Math.floor((right+left)/2)
       if(nums[mid]===target){
           return mid
       }else if(nums[mid]<target){
           left = mid + 1
       }else{
           right = mid -1
       }
    }
    return left
};

var merge = function(intervals) {
   intervals.sort((a,b)=>a[0]-b[0]) //升序排序
   return intervals.reduce((prev,cur)=>{
        let peek = prev[prev.length-1] // 获取到 prev 中最后一项
        if(peek && peek[1]>=cur[0]){ // 如果当前项和 peek 存在交集
            let left = peek[0]
            let right = peek[1]>cur[1]?peek[1]:cur[1]
            prev[prev.length-1]=[left,right] // 合并 peek 和 当前项
        }else{
            prev.push(cur)
        }
        return prev
   },[])
};