要求用回溯法求解8-皇后问题,使放置在8*8棋盘上的8个皇后彼此不受攻击,即:任何两个皇后都不在同一行、同一列或同一斜线上。请输出8皇后问题的所有可行解。
用回溯法编写一个递归程序解决如下装载问题:有n个集装箱要装上2艘载重分别为c1和c2的轮船,其中集装箱i的重量为wi(1≤ i ≤ n),且Σ𝑤𝑖≤𝑐1_+_𝑐2_𝑛𝑖=_1_。问是否有一个合理的装载方案可以将这n个集装箱装上这2艘轮船?如果有,请给出装载方案。
提示:参考子集和数问题的求解方法。
举例:当n=3,c1=c2=50,且w=[10,40,40]时,可以将集装箱1和2装到第一艘轮船上,集装箱3装到第二艘轮船上;如果w=[20,40,40]时,无法将这3个集装箱都装上轮船。
实验内容:
用回溯法编写一个递归程序解决如下装载问题:有n个集装箱要装上2艘载重分别为c1和c2的轮船,其中集装箱i的重量为wi(1≤ i ≤ n),且Σ𝑤𝑖≤𝑐1_+_𝑐2_𝑛𝑖=_1_。问是否有一个合理的装载方案可以将这n个集装箱装上这2艘轮船?如果有,请给出装载方案。
提示:参考子集和数问题的求解方法。
举例:当n=3,c1=c2=50,且w=[10,40,40]时,可以将集装箱1和2装到第一艘轮船上,集装箱3装到第二艘轮船上;如果w=[20,40,40]时,无法将这3个集装箱都装上轮船。
实验内容:
Transliteration
Yāoqiú yòng huísù fǎ qiújiě 8-huánghòu wèntí, shǐ fàngzhì zài 8*8 qípán shàng de 8 gè huánghòu bǐcǐ bù shòu gōngjí, jí: Rènhé liǎng gè huánghòu dōu bùzài tóngyī xíng, tóngyī liè huò tóngyī xié xiàn shàng. Qǐng shūchū 8 huánghòu wèntí de suǒyǒu kěxíng jiě.
Yòng huísù fǎ biānxiě yīgè dìguī chéngxù jiějué rúxià zhuāngzǎi wèntí: Yǒu n gè jízhuāngxiāng yào zhuāng shàng 2 sōu zàizhòng fēnbié wèi c1 hé c2 de lúnchuán, qízhōng jízhuāngxiāng i de zhòngliàng wèi wi(1≤ i ≤ n), qiě S𝑤𝑖≤𝑐1_+_𝑐2_𝑛𝑖=_1_. Wèn shìfǒu yǒu yīgè hélǐ de zhuāngzǎi fāng'àn kěyǐ jiāng zhè n gè jízhuāngxiāng zhuāng shàng zhè 2 sōu lúnchuán? Rúguǒ yǒu, qǐng gěi chū zhuāngzǎi fāng'àn.
Tíshì: Cānkǎo zǐ jí hé shù wèntí de qiújiě fāngfǎ.
Jǔlì: Dāng n=3,c1=c2=50, qiě w=[10,40,40] shí, kěyǐ jiāng jízhuāngxiāng 1 hé 2 zhuāng dào dì yī sōu lúnchuán shàng, jízhuāngxiāng 3 zhuāng dào dì èr sōu lúnchuán shàng; rúguǒ w=[20,40,40] shí, wúfǎ jiāng zhè 3 gè jízhuāngxiāng dōu zhuāng shàng lúnchuán.
Shíyàn nèiróng:
Yòng huísù fǎ biānxiě yīgè dìguī chéngxù jiějué rúxià zhuāngzǎi wèntí: Yǒu n gè jízhuāngxiāng yào zhuāng shàng 2 sōu zàizhòng fēnbié wèi c1 hé c2 de lúnchuán, qízhōng jízhuāngxiāng i de zhòngliàng wèi wi(1≤ i ≤ n), qiě S𝑤𝑖≤𝑐1_+_𝑐2_𝑛𝑖=_1_. Wèn shìfǒu yǒu yīgè hélǐ de zhuāngzǎi fāng'àn kěyǐ jiāng zhè n gè jízhuāngxiāng zhuāng shàng zhè 2 sōu lúnchuán? Rúguǒ yǒu, qǐng gěi chū zhuāngzǎi fāng'àn.
Tíshì: Cānkǎo zǐ jí hé shù wèntí de qiújiě fāngfǎ.
Jǔlì: Dāng n=3,c1=c2=50, qiě w=[10,40,40] shí, kěyǐ jiāng jízhuāngxiāng 1 hé 2 zhuāng dào dì yī sōu lúnchuán shàng, jízhuāngxiāng 3 zhuāng dào dì èr sōu lúnchuán shàng; rúguǒ w=[20,40,40] shí, wúfǎ jiāng zhè 3 gè jízhuāngxiāng dōu zhuāng shàng lúnchuán.
Shíyàn nèiróng:
实验原理:
- 要求用回溯法求解8-皇后问题,使放置在8*8棋盘上的8个皇后彼此不受攻击,即:任何两个皇后都不在同一行、同一列或同一斜线上。请输出8皇后问题的所有可行解。
- 用回溯法编写一个递归程序解决如下装载问题:有n个集装箱要装上2艘载重分别为c1和c2的轮船,其中集装箱i的重量为wi(1≤ i ≤ n),且Σ𝑤𝑖≤𝑐1_+_𝑐2_𝑛𝑖=_1_。问是否有一个合理的装载方案可以将这n个集装箱装上这2艘轮船?如果有,请给出装载方案。
- 提示:参考子集和数问题的求解方法。
- 举例:当n=3,c1=c2=50,且w=[10,40,40]时,可以将集装箱1和2装到第一艘轮船上,集装箱3装到第二艘轮船上;如果w=[20,40,40]时,无法将这3个集装箱都装上轮船。
实验内容:
1、8皇后问题
通过求解n-皇后问题,体会回溯法深度优先遍历状态空间树,并利用约束函数进行剪枝的算法思想。 代码实现:
-
#include <iostream> #include <cmath> using namespace std; bool Place(int k,int i,int *x){ //判定两个皇后是否在同一列或在同一斜线上 for(int j=0;j<k;j++) if ((x[j]==i)||(abs(x[j]-i)==abs(j-k))) return false; return true; } void NQueens(int k,int n,int *x){ //递归函数(求解n皇后问题) for (int i=0;i<n;i++){ if(Place(k,i,x)){ x[k]=i; if (k==n-1){ for (i=0;i<n;i++) cout<<x[i]<<" "; cout<<endl; } else{ NQueens(k+1,n,x); } } } } void NQueens(int n,int *x){ NQueens(0,n,x); } int main() { int x[8]; for (int i=0;i<8;i++) x[i]=-1; NQueens(8,x); return 0; }实验结果:
-
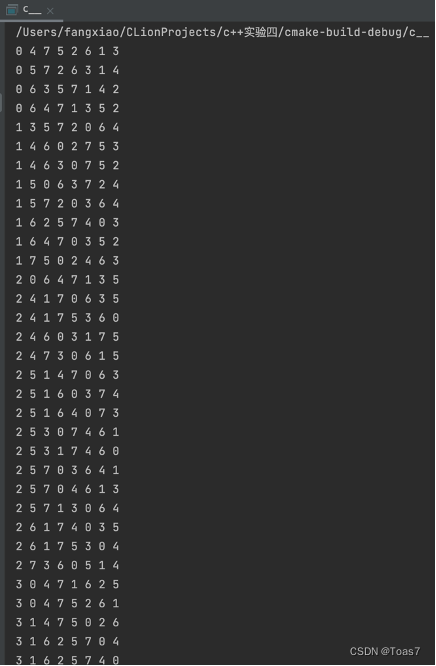
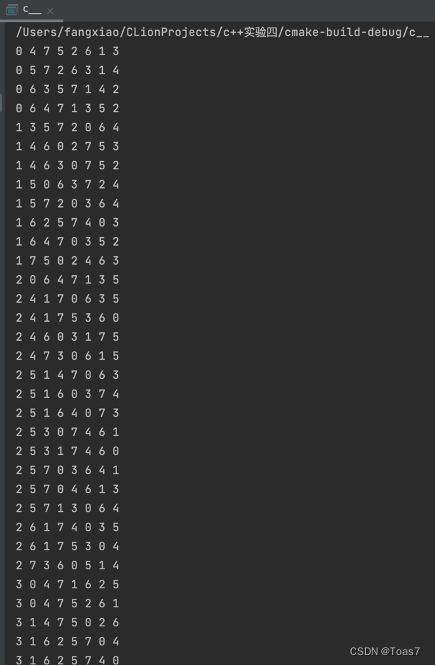
思考题1:请编程实现从n-皇后问题的所有92种可行解中筛选出12种独立解,而其余的解都可以由这些独立解利用对称性或旋转而得到。
#include <iostream> #include <cmath> #include <cstring> // 新增头文件用于调用 memcpy 函数 using namespace std; bool Place(int k,int i,int *x){ //判定两个皇后是否在同一列或在同一斜线上 for(int j=0;j<k;j++) if ((x[j]==i)||(abs(x[j]-i)==abs(j-k))) return false; return true; } bool IsEquivalent(int n, int *x, int *y) { // 判断两个解是否等价 for (int i =0; i < n; i++) { if (x[i] == n - y[i] - 1) return false; // 检查是否为旋转等价 false代表不相等 } for (int i = 0; i < n; i++) { // 检查是否为对称等价 if (x[i] == y[n - 1 - i]) return false; } return true; } void NQueens(int k,int n, int *x, int solutions[100][8], int &num){ //递归函数(求解n皇后问题) int i,j,h; for (i=0;i<n;i++){ if(Place(k,i,x)){ x[k]=i; if (k==n-1){ bool is_independent=true; for(j=0; j<num; j++){// 判断是否与已有解等价 if(IsEquivalent(n, x, solutions[j])){ is_independent = false; break; } } if(is_independent) { for (h = 0; h < n; h++){ solutions[num][h] = x[h]; } num++; } } else{ NQueens(k+1,n,x,solutions,num); } } } } void NQueens(int n,int *x,int solutions[100][8], int &num){ NQueens(0,n,x,solutions,num); } int main() { int x[8]; for (int i=0;i<8;i++) x[i]=-1; int solutions[100][8]; int num_solutions = 0; NQueens(0,8,x,solutions,num_solutions); //NQueens(8,x, solutions,num_solutions); cout << "共找到 " << num_solutions << " 种独立解:" << endl; for (int i = 0; i < num_solutions; i++) { cout << "解 " << i + 1 << ": "; for (int j = 0; j < 8; j++) { cout << solutions[i][j] << " "; } cout << endl; } return 0; }实验结果:
-
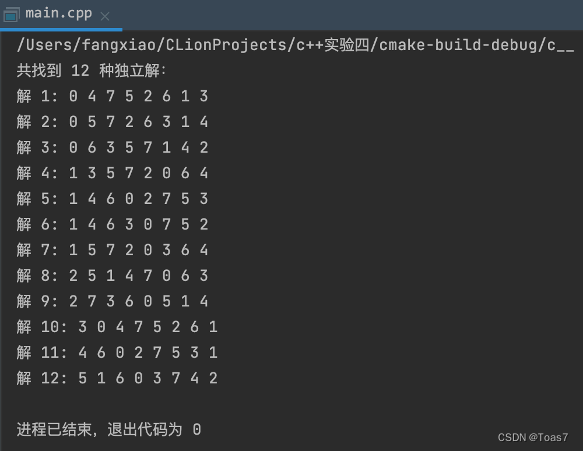
思考题2: 若n-皇后问题要求在求得第一个可行解之后算法即终止,请编程实现。
代码:
#include <iostream>
#include <cmath>
using namespace std;
bool Place(int k,int i,int *x){ //判定两个皇后是否在同一列或在同一斜线上
for(int j=0;j<k;j++)
if ((x[j]==i)||(abs(x[j]-i)==abs(j-k)))
return false;
return true;
}
bool NQueens(int k,int n,int *x){ //递归函数(求解n皇后问题)
for (int i=0;i<n;i++){
if(Place(k,i,x)){
x[k]=i;
if (k==n-1){
for (i=0;i<n;i++) cout<<x[i]<<" ";
cout<<endl;
return true;
}
if(NQueens(k+1,n,x))
return true;
}
}
return false;
}
void NQueens(int n,int *x){
NQueens(0,n,x);
}
int main()
{
int x[8];
for (int i=0;i<8;i++)
x[i]=-1;
NQueens(8,x);
return 0;
}
运行结果:
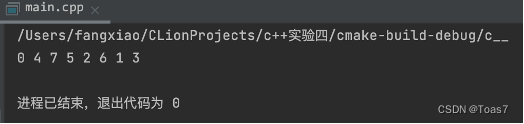
2、装载问题
算法实现主体部分已给出,请补充完整,并使用下面三个测试案例调试通过。
第一艘船载重60,第二艘船载重40,5个集装箱重量分别为:
(1)22 35 24 19 4
(2)22 35 24 15 4
(3)22 35 24 15 3
代码实现:运行结果:
#include <iostream>
#include <cmath>
#include <cstring> // 新增头文件用于调用 memcpy 函数
using namespace std;
class Loading {
private:
int n, //集装箱数
*x, //当前解
*bestx; //当前第一艘船的最优解
int c1, //第一艘轮船的核定载重量
c2, //第二艘轮船的核定载重量
*w, //集装箱重量数组
total, //所有集装箱重量之和
cw, //当前第一艘船的载重量
bestw, //当前第一艘船的最优载重量
r; //剩余集装箱总重量
public:
Loading() //构造函数
{
n = 5;
x = new int[n+1];
bestx = new int[n+1];
w = new int[n+1];
c1 = 60;
c2 = 40;
w[1] = 22;
w[2] = 35;
w[3] = 24;
w[4] = 19;
w[5] = 4;
total = w[1]+w[2]+w[3]+w[4]+w[5];
r = total;
bestw = 0;
}
~Loading() //析构函数
{
delete[] x;
delete[] bestx;
delete[] w;
}
void Backtrack(int i); //找到最接近第一艘轮船载重c1的最佳装载方案,
//最优载重值bestw,最优解数组bestx。
void Show();//输出整个装载方案
};
void Loading::Backtrack(int i)
{ //搜索第i层结点
if (i>n)
{//到达叶节点
if (cw>bestw)
{
for (int j=1;j<=n;j++) bestx[j]=x[j];
bestw=cw;
}
return;
}
//搜索子树
r-=w[i];
if (cw+w[i]<=c1) //x[i]=1时的可行解约束条件
{//搜索左子树
x[i]=1;
cw+=w[i];
Backtrack(i+1);
cw-=w[i];
}
if (cw+r>bestw) //x[i]=0时增加的约束函数,剪去不含最优解的分枝
{//搜索右子树
x[i]=0;
Backtrack(i+1);
}
r+=w[i];
}
void Loading::Show()
{
cout << "装载方案:" << endl;
cout << "第一艘船:";
for (int i = 1; i <= n; i++)
{
if (bestx[i] == 1)
{
cout << w[i] << " ";
}
}
cout << endl;
cout << "第二艘船:";
for (int i = 1; i <= n; i++)
{
if (bestx[i] == 0)
{
cout << w[i] << " ";
}
}
cout << endl;
cout << "第一艘船最优载重量:" << bestw << endl;
}
int main()
{
Loading ld;
ld.Backtrack(1);
ld.Show();
system("pause");
return 0;
}
运行结果:
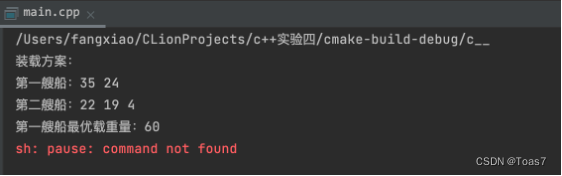
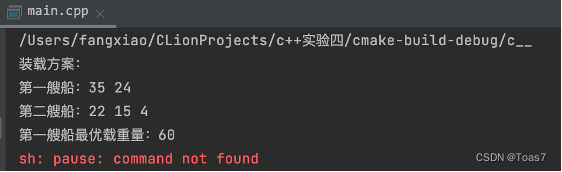
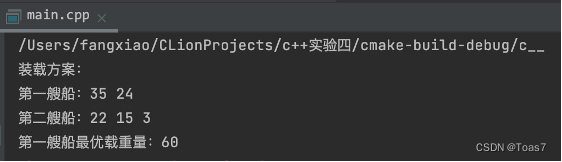
思考题3:求上面回溯法求解装载问题的计算时间复杂度?有什么方法可以继续改进算法的时间复杂度?
由于bestx可能被更新O(2^n)次,因此该算法的时间复杂度是O(n2^n)。
改进策略可以有下面两种,均可将算法的时间复杂度降为O(2^n):
(1) 首先运行只计算最优值的算法,计算出最优装载量W,所耗时间O(2^n)。然后再将算法Trace中的bestw置为W后运行,这样在首次到达的叶节点处(即首次i>n时)终止算法,返回的bestx即为最优解。
(2) 另一种策略是在算法中动态的更新bestx。在第i层的当前结点处,当前最优解由x[j],1≤j<i和best[j],i≤j≤n所组成。每当算法回溯一层时,将x[i]存入bestx[i]。
思考题4:请用非递归的迭代回溯方式,重新实现装载问题的求解。
代码:
#include <iostream>
#include <cmath>
#include <cstring>
using namespace std;
class Loading {
private:
int n; // 集装箱数
int *x; // 当前解
int *bestx; // 当前第一艘船的最优解
int c1; // 第一艘轮船的核定载重量
int c2; // 第二艘轮船的核定载重量
int *w; // 集装箱重量数组
int total; // 所有集装箱重量之和
int cw; // 当前第一艘船的载重量
int bestw; // 当前第一艘船的最优载重量
int r; // 剩余集装箱总重量
public:
Loading() // 构造函数
{
n = 5;
x = new int[n + 1];
bestx = new int[n + 1];
w = new int[n + 1];
c1 = 60;
c2 = 40;
w[1] = 22;
w[2] = 35;
w[3] = 24;
w[4] = 19;
w[5] = 4;
total = w[1] + w[2] + w[3] + w[4] + w[5];
r = total;
bestw = 0;
}
~Loading() // 析构函数
{
delete[] x;
delete[] bestx;
delete[] w;
}
void Backtrack(); // 找到最接近第一艘轮船载重c1的最佳装载方案,最优载重值bestw,最优解数组bestx。
void Show(); // 输出整个装载方案
};
void Loading::Backtrack()
{
int i = 1;
while (i > 0)
{
if (i > n)
{
// 找到更优的装载方案
if (cw > bestw)
{
memcpy(bestx, x, (n + 1) * sizeof(int));
bestw = cw;
}
// 回溯到上一个箱子位置
i--;
while (i > 0 && x[i] == 0)
{
cw -= w[i];
r += w[i];
i--;
}
// 如果仍有箱子可选,则放置到第二艘船上
if (i > 0)
{
x[i] = 0;
cw -= w[i];
r += w[i];
}
}
else
{
// 尝试将箱子放置到第一艘船上
if (cw + w[i] <= c1)
{
x[i] = 1;
cw += w[i];
r -= w[i];
i++;
}
else
{
// 将箱子放置到第二艘船上
x[i] = 0;
r -= w[i];
i++;
}
}
}
}
void Loading::Show()
{
cout << "装载方案:" << endl;
cout << "第一艘船:";
for (int i = 1; i <= n; i++)
{
if (bestx[i] == 1)
{
cout << w[i] << " ";
}
}
cout << endl;
cout << "第二艘船:";
for (int i = 1; i <= n; i++)
{
if (bestx[i] == 0)
{
cout << w[i] << " ";
}
}
cout << endl;
cout << "第一艘船最优载重量:" << bestw << endl;
}
int main()
{
Loading ld;
ld.Backtrack();
ld.Show();
return 0;
}
运行结果
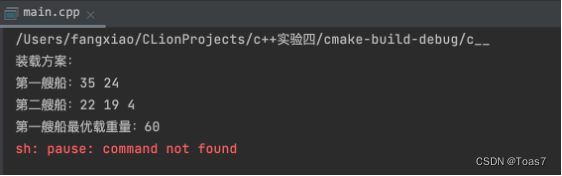
码字不易,都看到这了,欢迎打赏!!