作者简介:大家好,我是未央;
博客首页:未央.303
系列专栏:Java初阶数据结构
每日一句:人的一生,可以有所作为的时机只有一次,那就是现在!!!
文章目录
一、直接插入排序算法
1.1 算法思路
1.2 算法图解过程
1.3 算法代码
1.4 算法特征总结
二、希尔排序
2.1 算法思路
2.2 算法图解过
2.3 算法代码程
2.4 算法特征总结
总结
前言
今天我们将进入到算法的几种常见算法当中,我们首先介绍两种数据结构中最常用的直接插入排序和希尔排序算法;这些经典的排序算法我们必须要熟练的掌握和运用;
一、直接插入排序算法
1.1 算法思路
从数组的第二个元素开始,为把该元素放到前面合适的位置上(在这个过程中可能需要移动前面的元素,给要插入的元素腾出位置)
举例说明:
当插入第i(i>=1)个元素时,前面的array[0],array[1],…,array[i-1]已经排好序,此时用array[i]的排序码与array[i-1],array[i-2],…的排序码顺序进行比较,找到插入位置即将array[i]插入,原来位置上的元素顺序后移
1.2 算法图解过程
1.3 算法代码
/** * 直接插入排序 * @param array */ public static void insertSort(int[] array) { for (int i = 1; i < array.length; i++) { int tmp = array[i]; int j = i - 1; for (; j >= 0; --j) { // [32、56、12、23],i指向12,j一开始指向56,我们就是借助tmp和j的变化,把32、56向后移动一位,把12放到他们前面 // 这个过程就像把array[i](tmp)插入到数组,放到数组中合适的位置,保证放完后数组是升序(所以才要a[j + 1] = a[j]不断的移动a[j]的位置 if (tmp < array[j]) { array[j + 1] = array[j]; // 如果a[j]的值大于a[i](tmp),说明a[i]应该放到a[j]前面——a[j]应该向后移动 } else { break; // 此时说明a[j]已经在合适的位置了,不用再次移动了 } } array[j + 1] = tmp; // 注意这里不能等于array[i],因为经过上面array[j+1] = array[j]数组的移动,array[i]已经发生了变化 } }
1.4 算法特征总结
- 元素集合越接近有序,直接插入排序算法的时间效率越高
- 时间复杂度:O(N^2)(最好情况下-即当数组有序时O(n))
- 空间复杂度:O(1),它是一种稳定的排序算法

二、希尔排序
2.1 算法思路
希尔排序法又称缩小增量法。希尔排序法的基本思想是:把数据分组,然后再每一组内用直接插入排序对该组的数据进行排序,对每个排完序后再对整个数组进行直接插入排序。
为什么要这样做呢?
上面刚提到过:直接插入排序适合对接近有序的数组进行排序,元素集合越接近有序,直接插入排序的时间效率越高。那么我们就先通过分组排序让这个数组进可能的接近有序,然后不就相当于优化了直接插入排序了吗?
总的来说,希尔排序可以分为两个部分:
- 预排序(分组排序,使得数组尽可能趋近有序)
- 直接插入排序
举例说明:
假如有这样一个乱序数组:
解析:
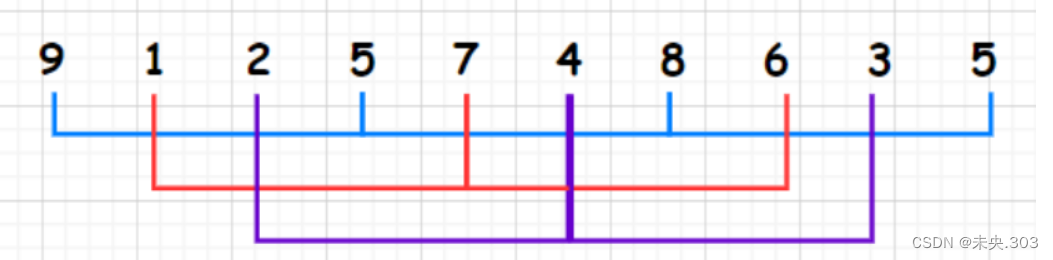
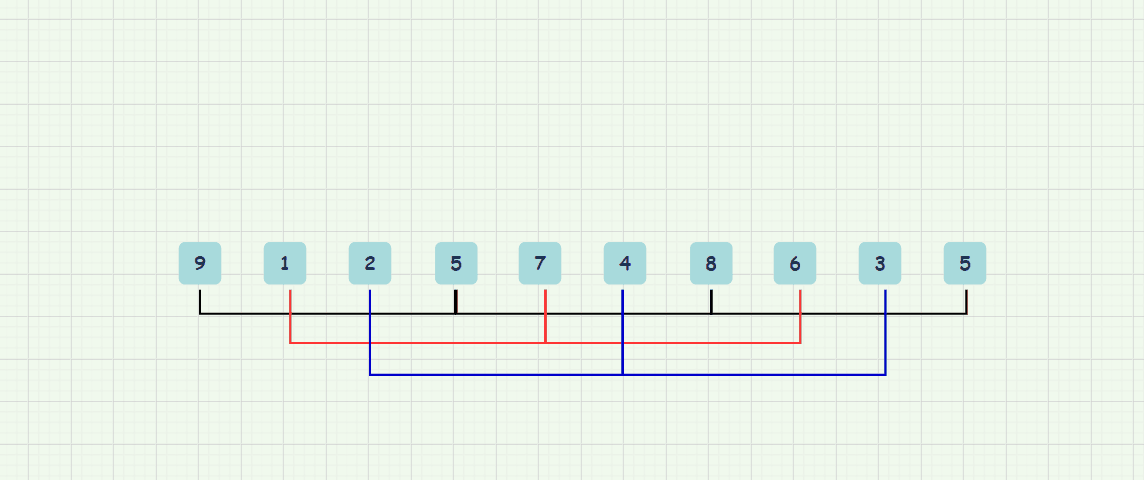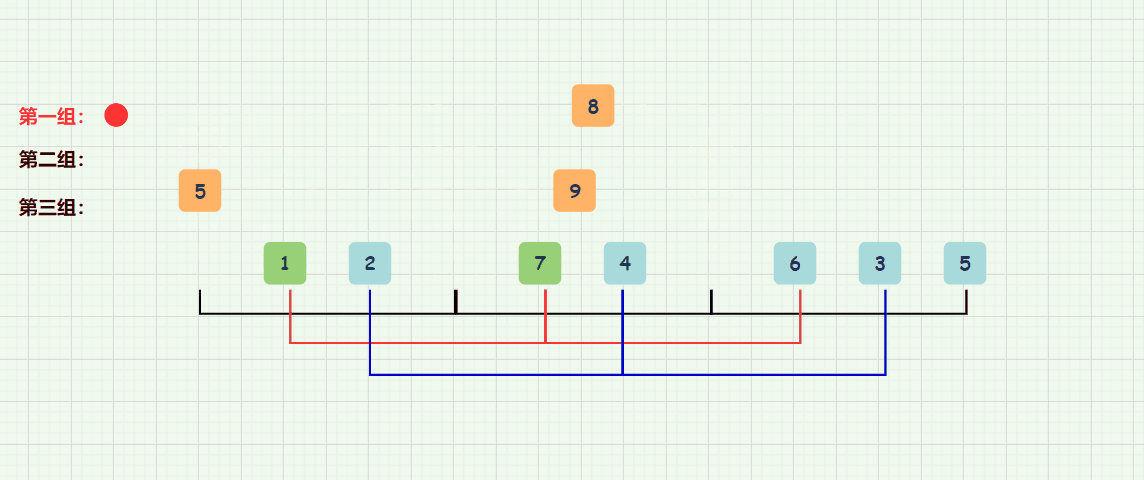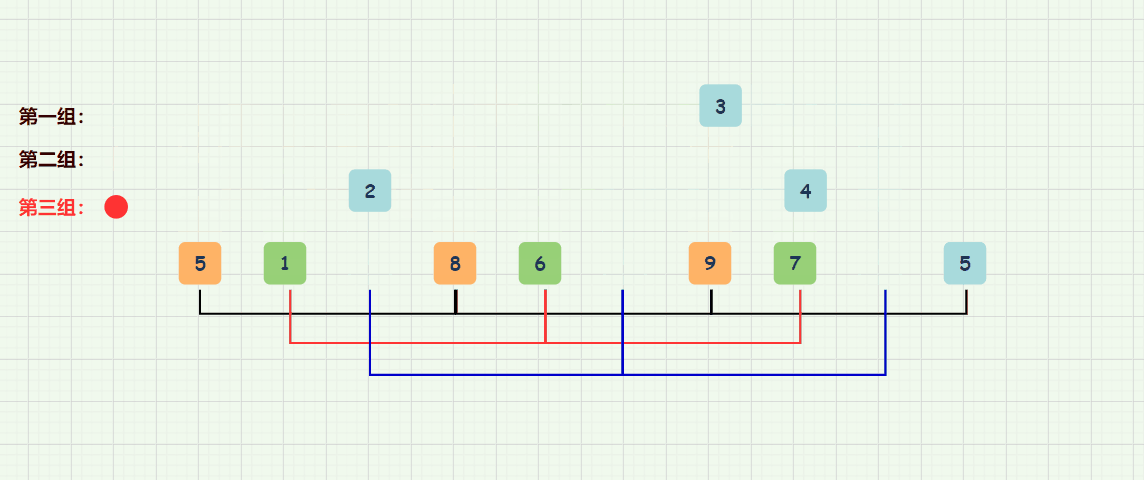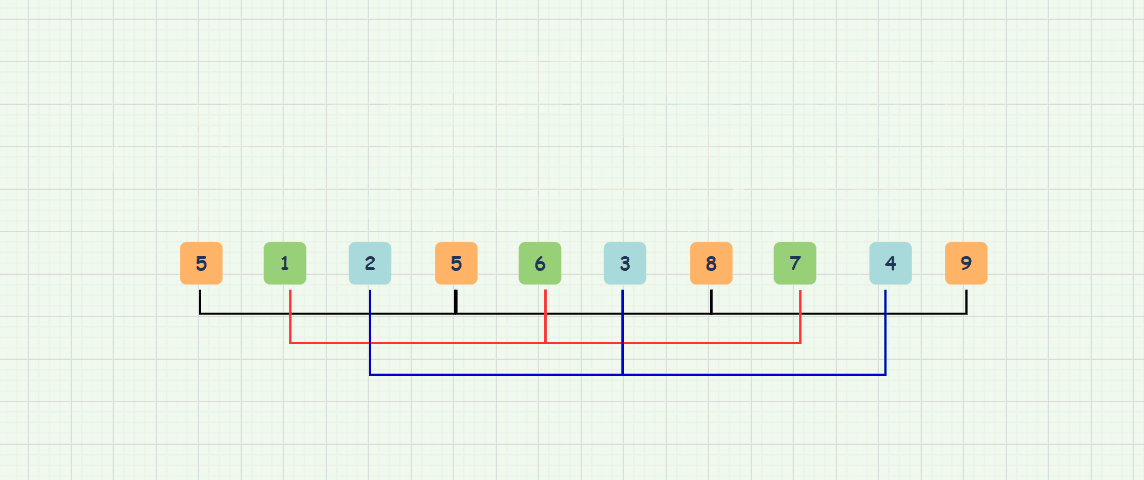
我们一开始分为3组——即gap(间隔为3),然后对这分别对这三组进行排序;
【9,5,8,5】这4个数就分为一组,【1,7,6】这3个数分为一组,【2,4,3】分为一组。总来说:gap为几,这里就会分割成几组数据。要注意每个组他们元素下标差都是gap。
接下来就以插入排序的思想对这三组分别进行排序。
既然是分组进行插入排序,那就好办了,像第一组:【9,5,8,5】排序后为【5,5,8,9】,第二组【1,7,6】排序后为【1,6,7】,第三组【2,4,3】排序后为【2,3,4】,如图所示:
2.2 算法图解过程
2.3 算法代码
// 希尔排序——预排序(gap,表示分的组数) private static void shell(int[] array, int gap) { for (int i = gap; i < array.length; i++) { int tmp = array[i]; int j = i - gap; for (; j >= 0; j = j - gap) { if (tmp < array[j]) { array[j + gap] = array[j]; // 如果a[j]的值大于a[i](tmp),说明a[i]应该放到a[j]前面——a[j]应该向后移动 } else { break; // 此时说明a[j]已经在合适的位置了,不用再次移动了 } } array[j + gap] = tmp; // 注意这里不能等于array[i],因为经过上面array[j+gap] = array[j]数组的移动,array[i]已经发生了变化 } }我们可以分成把要排序的数组分成不同的组(gap取不同的值)——进行多次预排序,这样我们的数组会更加接近有序;
注意:当gap == 1时,其实就是直接插入排序;

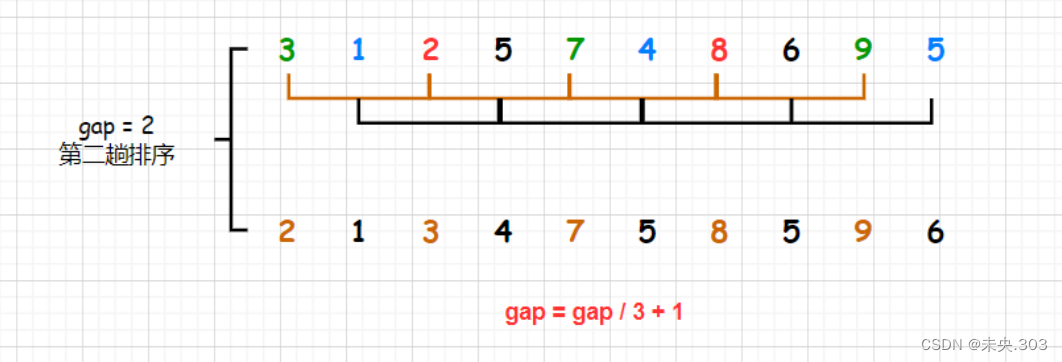
 相应的代码就是:
相应的代码就是:
public class Test3 {
// 希尔排序——预排序(gap,表示分的组数)
private static void shell(int[] array, int gap) {
for (int i = gap; i < array.length; i++) {
int tmp = array[i];
int j = i - gap;
for (; j >= 0; j = j - gap) {
if (tmp < array[j]) {
array[j + gap] = array[j]; // 如果a[j]的值大于a[i](tmp),说明a[i]应该放到a[j]前面——a[j]应该向后移动
}
else {
break; // 此时说明a[j]已经在合适的位置了,不用再次移动了
}
}
array[j + gap] = tmp; // 注意这里不能等于array[i],因为经过上面array[j+gap] = array[j]数组的移动,array[i]已经发生了变化
}
}
/**
* 希尔排序——直接插入排序的优化
* @param array
*/
public static void shellSort(int[] array) {
for (int i =array. length / 3 + 1; i > 1; i = i / 3 + 1) {
shell(array, i); // 预排序,让我们排序的这个数组接近有序,这样下面的直接插入排序shell(array,1)时间效率才会高
}
shell(array, 1); // 这个相当于把数组分成一组,其实就是我们上面写的直接插入排序
}
public static void main(String[] args) {
int[] a = {9, 1, 2, 5, 7, 4, 8, 6, 3, 5};
shellSort(a);
System.out.println("排序后的数组为:" + Arrays.toString(a));
}
}运行结果:
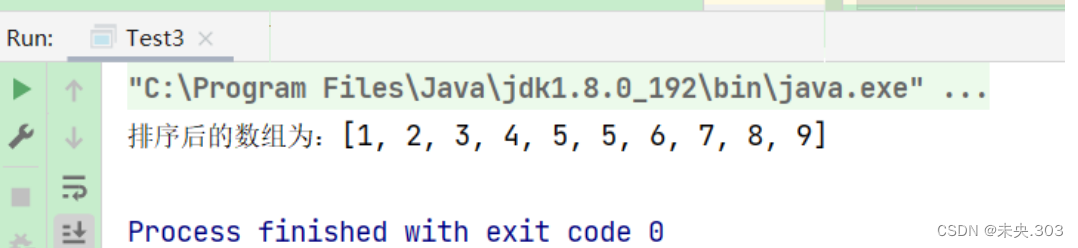
2.4 算法特征总结
1、希尔排序是对直接插入排序的优化。
2、当gap > 1时都是预排序,目的是让数组更接近于有序。当gap == 1时,数组已经接近有序的了,这样就会很快。这样整体而言,可以达到优化的效果。我们实现后可以进行性能测试的对比。
3、稳定性:不稳定
4、时间复杂度:排序的时间复杂度不好计算,因为gap的取值方法很多,导致很难去计算。
总结
本节内容的两个算法就介绍到这里了,下一节内容我们将介绍其他两种算法,让我们继续期待下一节的内容吧!!!!!!!!!!!!!