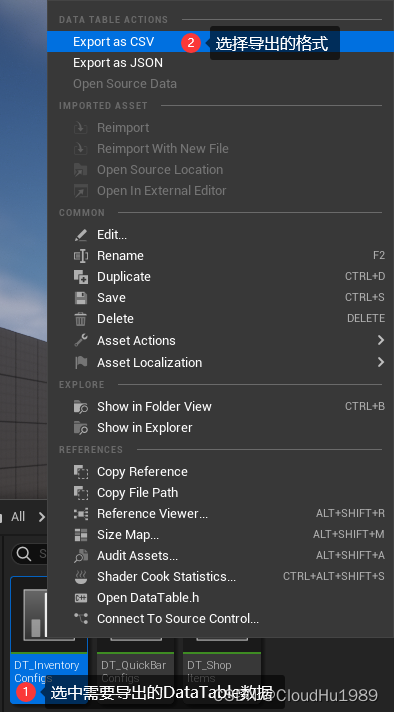
说明

最近想探讨一下毫米波雷达测量准确度及其改善的问题，这个话题下可供讨论的问题有很多，蒙特卡罗方法(或者说基于蒙特卡罗方法对测量准确度以及精度的评估)是其中之一，该方法是一个十分有效的工具，在科研(发paper)上也是不可少的。在探讨测量的准确度之前，我将先分解并讨论几个小的话题，最后以测量准确度的话题进行汇总。本博文试图捋清楚蒙特卡罗方法及其在信号处理中的应用。

Blog

20230520 博文第一次写作

谨以此文献给墨の宝，感谢投喂午餐！祝520快乐！

一、什么是蒙特卡罗方法

该方法是一种关于概率的实验方法，是由冯诺依曼和乌拉姆等人发明的，蒙特卡罗这个名字取自摩纳哥的蒙特卡罗赌场。那么，什么是关于概率的实验方法？它的本质是利用事件发生的频率作为事件发生概率的近似值。举个例子：

图1.1 蒙特卡罗方法讲解示例图

上图中假设我们不知道圆面积的计算公式，或者知道公式是pi*r^2，但是不知道pi的具体值，(总之我们没法用数值计算的方法得到圆的面积)，此时怎么得出圆的面积是多少？一种可行的方法是：用概率的方法推得面积，如果我们在正方形的整个区域内随机生成散点，比如总共随机生成了N个点，然后其中有M个点落在了圆形区域内，那么落在圆形区域的频率为M/N,不难理解的是，当我们实验的次数N足够多，M/N的值会接近于（圆的面积÷正方形的面积），该值也是散点落在圆中的概率，此时我们可以用正方形的面积*(M/N)得到圆的面积。

再回到我们前文那句话：它的本质是利用事件发生的频率作为事件发生概率的近似值，上面的例子对这句话做出了解释，相信已经不难理解了。此外，实验的次数需要越多越好(次数越多频率才越接近真实的概率值)，这其实和我们高中学概率知识时老师常举的例子类似：当你掷硬币的次数足够多时，硬币正面朝上总次数必然等于所掷次数的一半。

关于上面的例子，我也写仿真了一下。算法概述和流程为：以圆的中心作为坐标原点，分别在x、y为（-1 1）的范围内随机生成：10、100、100000个点，并判断这些点离坐标原点的距离是否小于或等于1(是，则位于圆内)，基于处于圆内的频率*正方形的面积来得到圆的面积。(代码见博文第六章的链接，后面章节的仿真代码我也一同上传了) 。得到的结果如下：

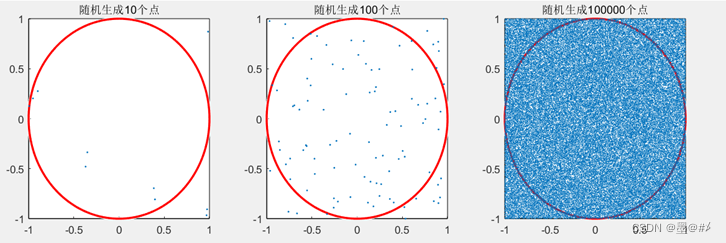
图1.2 在正方形区域内随机生成的点结果图

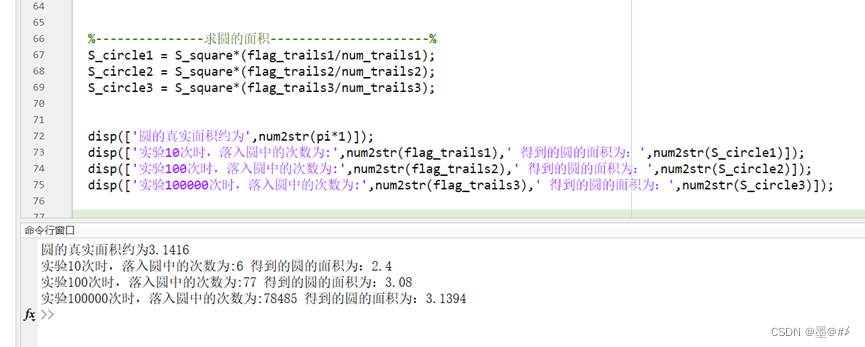
图1.3 基于蒙特卡罗方法求解圆面积的结果

可以看到，实验的次数越多，得到的结果越准确(接近真实值)。

二、蒙特卡罗方法在信号处理与算法验证中的作用

前文第一章讲清楚了该方法是什么以及怎么用。该方法和信号处理以及算法验证扯上关系主要是我们可以通过这种方法背后的思想(多次随机试验)来评估信号处理或算法的准确度以及精度。

它的应用场景有很多，这里以车载毫米波雷达的测角算法(关于测角可以参考我之前的博文：车载毫米波雷达DOA估计综述_墨@#≯的博客-CSDN博客)为例说说它的应用。

比如我们要去评估DBF算法在雷达视场范围内的测角精度和准确度，那么我们可以在视场范围内的每个角度下进行N次蒙特卡罗试验，看看DBF下的测量结果与真实值的差异，并进而得到测量的精度和准确度。

或者，我们可以去评估不同SNR下使用DBF算法时测量结果的准确度。此时针对特定的SNR，在视场范围内随机生成N次目标，看看DBF下的测量结果与真实值的差异，并进而得到不同SNR下使用DBF算法测量时的准确度。

后文第三章分别对前述这两种情况进行仿真。

三、基于蒙特卡罗方法对车载毫米波雷达测角算法的评估

进入后文仿真的内容之前，先弄清楚两个简单的概念：准确度(accuracy)和精度(precision)。这两个概念应该是关于测量准确度那篇博文中的内容，但是这里需要用到，于是先捋一下。

在做测量时，准确度是我们用以衡量测量值和真实值之间差值大小的一个概念，精度是我们用以衡量测量值之间(各测量值和测量值的均值)离散程度的一个概念。以射箭为例，假如靶心是我们的真实值(10分)，而我们每次射箭都偏了几环，射在7分左右，此时可以说我们的准确度不好但是精度不错。准确度和精度是两个独立的概念。

更具体地，我们可以用RMSE(Root Mean Square Error)均方根误差对测量的准确度进行定量，用SD（Standard Deviation）标准差来定量测量的精度。

（3-1）

(3-2)

3.1 评估特定SNR值时，不同角度下，DBF测角算法的准确度和精度

1、实验说明：

设定雷达视场范围(测角范围)为±75°，以1°为步进，每度进行100次蒙特卡罗实验，看看DBF算法下不同角度下测量结果的准确度和精度。仿真中，目标的SNR值取12dB，测角阵列为8阵元间隔0.5个波长的均匀阵。

2、实验结果

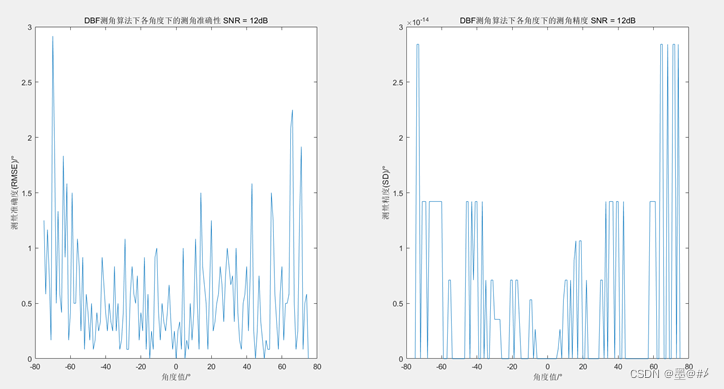
图3.1 基于蒙特卡罗方法评估不同角度下DBF测角算法的准确度和精度结果

3、实验小结

从上图可以看到，从大角度接近0°时，RMSE和SD整体来看都是在减小的，阵列的分辨率与孔径大小和目标所在角度有关：

（3-3）

当在阵列法线方向时，θ= 0°，此时θres最小，理论上来说测量的准确度和精度都会增加。实验结果与理论是相符合的。

3.2 评估不同SNR下，DBF测角算法的准确度

1、实验说明：

以5dB为起始SNR值，以2dB为步进，直到55dB。在±75°范围内随机生成1000个目标，看看不同SNR值下，DBF测角算法的准确度。仿真中，测角阵列为8阵元间隔0.5个波长的均匀阵。因为这里是随机生成不同的角度，所以没法求解精度，这里只评估准确度。

2、实验结果

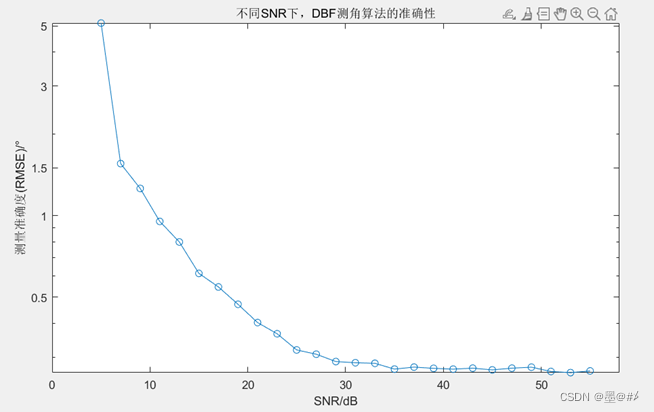
图3.2 基于蒙特卡罗方法评估不同SNR下DBF测角算法的准确度

3、实验小结

从图中可以看到测量的准确度随着SNR的增加有很明显的改善。测量的准确度主要取决于两个因素：分辨率和SNR，这在本章的实验中有了很好的体现，不过更具体的我将在后面关于测量准确度的博文中给出分析。

四、总结

本博文试图捋清楚蒙特卡罗方法及其在信号处理中的应用。首先简单介绍了蒙特卡罗方法，并基于该方法进行了求正方形内圆面积的仿真验证，随后探讨了该方法在信号处理中的应用，并以DBF测角算法为例，分别仿真评估了特定SNR值下，DBF算法在不同角度下测量的准确度和精度、以及在不同SNR值下，DBF测角算法的准确度。

蒙特卡罗方法是一个很好且很实用的工具，本博文中所有的仿真代码见所附的参考资料链接，代码中很多的参数读者可以自行修改，探讨其它参数(比如阵列孔径)下，DBF测角算法的准确度等。本博文如有不妥或需要补充的地方欢迎读者评论，我会不定期更新，我们一起维护。