加法法则 --每一类都能够独立的完成任务

乘法法则 --集合论 任务分步骤

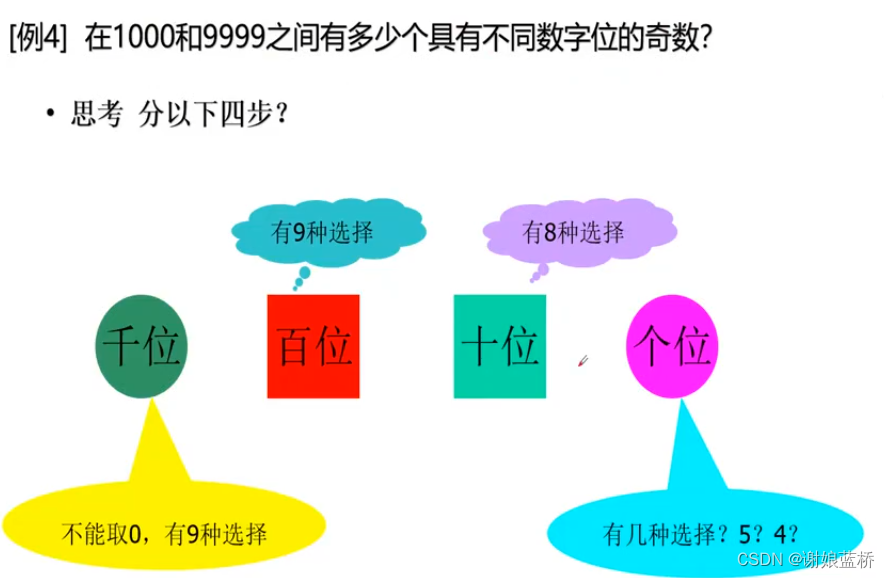
1000和9999之间有多个具有不同数位的奇数

个位可能是 1 3 5 7 9 5可能
千位可能是 1-9 9种可能减去个位的一种可能 即为 8种
百位是 8种
十位是 7种
总共 5887 =5640=2240种

n = 7${}^3+11^2+13^4$ 求除尽n的整数个数

每个因子的形式是 $7^m+11^n+13^k$
m只能是0 1 2 3 4种可能
n是 0 1 2 3种可能
k 是0 1 2 3 4 5种可能
则整体个数为 435=60种

0到10000之间有多少个整数恰好是有一位数字是5

证明只有1个位是5
个位 999
十位999
百位 999
千位 999
则整体是 4999 =- 2916种

两位数字可以组成多少两位互异且非零的两位数

$a\ne b;a\ne 0;b\ne 0$

9*8=72种

个位是0的 9个 01 02 03 04 05 06 07 08 09
十位是0的 9个 10 20 30 40 50 60 70 80 90
两个数相同的 10个 00 11 22 33 44 55 66 77 88 99
100 -(9+9+10)=72

减法法则 全集-补集

求小于10000 的含1的正整数

不含1的正整数 可以看做4位数，但 0000 除外
个 十 百 千 各个有9中可能 999*9 -1 =6560
则小于10000正整数有9999个
则结果为 9999 - 6560 =3439 个

求小于10000 的含0的正整数
不含0的一位数 9
两位数99=81
三位数999=729
四位数9999=6561
含0的正整数 9999 - 6561 -729 -81 -9 =2619

除法法则

取书

1. 日文+英文 57=35
   日文+ 中文 105=50
   英文+中文 7*10=70
   则总共 155种
2. 两本日文 $C_5^2$ =10
   两本英文 $C_7^2$=21
   两本中文 $C_1{0}^2$ =45
   则总共 152/2 = 76种
   3.$C_{22}^2=22\ast 21/2=11\ast 21=231种$

一一对应 冠军比赛 淘汰赛

Cayley定理 n个有标号的顶点的树的数目等于$n^{n-2}$

一个当树根
n个已知顶点 用n-1条边连接起来的连通图
将n个城市连接起来的树状公路有 $n^{n-2}$种可能方案

$$600=2\ast 3\ast 100=5\ast 5\ast 2\ast 2\ast 2\ast 3$$
$$=5^2\ast 2^3\ast 3^1$$
$$3\ast 4\ast 2=24种$$

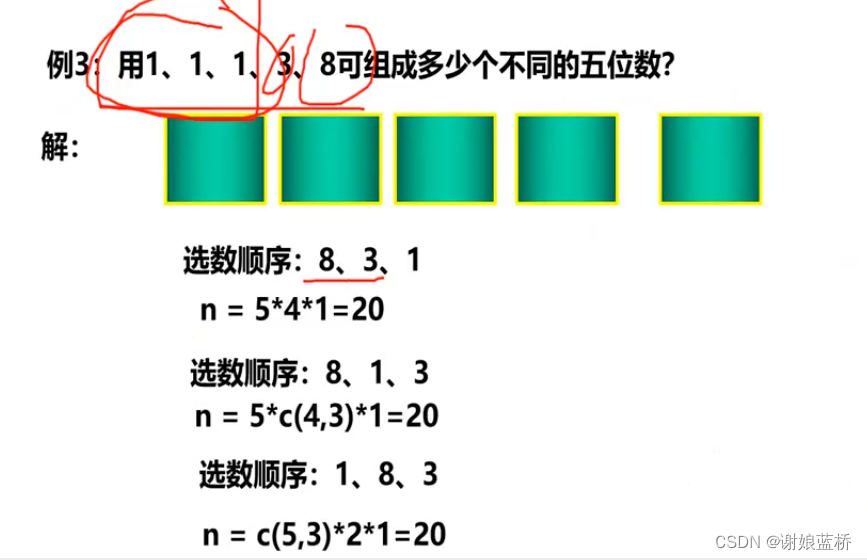
1.8有5中可能 3有4中可能 1就一种 5* 4 * 3 =20
2.8 1 3 8有5种可能 ，1有$C_4^3=4$ 3有一种 5 * 4 * 1 =20
3.1可能 $C_5^3=10种$ 8有两种 3有一种 10 * 2* 1 =20
总共有60种

集合排列

r排列 全排序 球不同，盒子不同，盒子不空

$P(n,r)=\frac{n!}{(n-r)!}=m!\ast C_n^m=A_n^r=n\ast n(n-1)\ast ...\ast (n-r+1)$

$A_5^2=5\ast 4=20$种旗子的选法
$3!\ast C_{20}^3=6\ast 20\ast 19\ast 18÷6=6840$
则整体方案是 20*6840 = 136800

男生全排列
女生插空

1. 千位 选 2，4 千位有两种可能 个位有 0 2/4 6 8 4 种可能 2* 4 * $A_8^2$
2. 千位选 3 千位1种 个位5种 5 * $A_8^2$
   （8 + 5 ）* 8 * 7 = 56 * 13=728
   

r 组合 $C_n^r=\frac{n!}{r!(n-r)!}=\frac{A_n^r}{r!}$ 球不同 盒子相同 无空盒

$C_{12}^5-C_{10}^3$ = 672

mod 3 = 1 100种
mod3 = 2 100种
mod3 = 0 100种
1）3个数属于mod1
2）3个数属于mod2
3）3个数属于mod3
3*$C_{100}^3$
4) 各取一个
$100^3$
3*$C_{100}^3$+$100^3$ = 485100+1000000 = 1485100

圆排列 $\frac{P(n,r)}{r}=\frac{n!}{r(n-r)!}$ 特别的 $\frac{n!}{n}=(n-1)!$

1)7！-2*6! = 5 * 6! = 3600
8个人 7! 种排列 AB在一起 当一个人 6！ 排列 AB 在一起 有两种可能

2. 5个空 5 * 4 * 3 * 4!=60 * 5 * 4 * 3 * 2 =7200

9！ - 2 * 8! = 6 * 8! = 241,920‬

每对夫妻 有两种可能，n对夫妻 有 $2^n$种可能
n对夫妻圆排 （n-1)!
则共有 $2^n\ast (n-1)!$

项链排列 $\frac{P(n,r)}{2r}=\frac{n!}{2\ast r\ast (n-r)!}$ 特别的 (n-1)!/2

圆排基础上正反面顺序一致


19!/2

重排列

4m 3n 2r 5q
$\frac{14!}{4!\ast 3!\ast 2!\ast 5!}$


S = {$2\ast A,B,3\ast C$}
2A 0B 3C $\frac{5!}{2!\ast 3!}$ =10

2A 1B 2C $\frac{5!}{2!\ast 2!}$ =30

1A 1B 3C $\frac{5!}{3!}$=20
总共60种

1M 4S 4I 2P
$\frac{11!}{4!\ast 4!\ast 2!}$


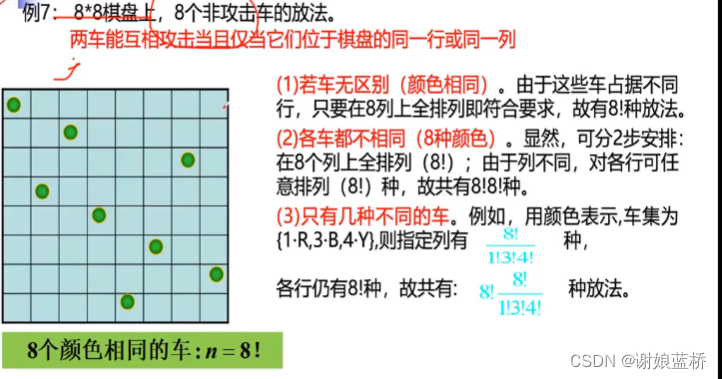
K个颜色的n个车 $\frac{n{!}^2}{n_1!\ast n_2!\ast n_3!\ast \ast \ast n_k!}$

Stringling 公式 n! 的近似值

Stringling 是求 n! 的近似公式

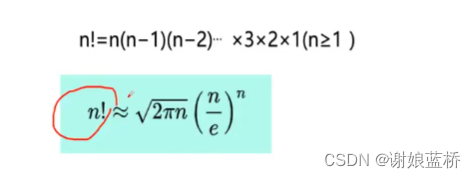
n! $\approx \sqrt{2\ast \pi \ast n}\ast (\frac{n}{e}{)}^n$

重复组合 $C_{r+k-1}^r=C_{r+k-1}^{k-1}$

所有元素重复数不小于r

不相邻组合 $C_{n-r+1}^r$

全排列的生成算法–了解

序数法