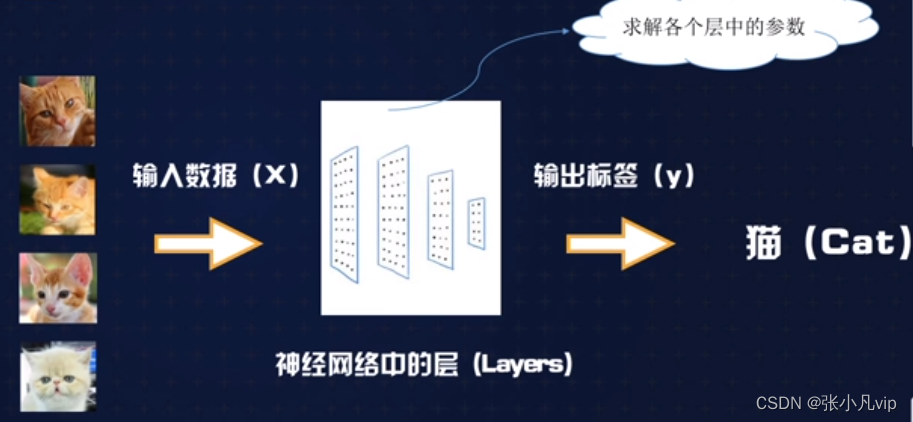
机器学习是将输入(比如图像)映射到目标(比如标签“猫”),并建立映射规则(即模型)。在深度学习中,神经网络通过一系列数据变换层来实现这种输入到目标的映射,本章节我们具体来看这种学习过程是如何实现的。
学习内容
1、理解层(Layer)及权重(weight)的概念及作用
2、理解损失函数(Loss function)的作用
3、理解优化器(optimizer)的作用、了解反向传播(back propagation)过程以及梯度下降
4、理解神经网络的工作原理
5、了解常见的神经网络架构
神经网络本质上是一个求解智数的多层数学框架
神经网络的本质是一个求解数的多层数学框架。以图像识别为例,建立一个“猫脸识别”神经网络模型的过程,实际上类似手求一个复合函数的智数:
求解f(x)= y的参数(也叫做权重)
其中,x =(多张猫的图片)
y =猫(即标签)
例如: 输入以下多张图片

神经网络最终得出的是输入数据(如照片)和预期输出标签(如猫)之间的映射规则(核心是权重参数)。
理解神经网络的基本单元——神经元
神经网络的每个层中包括一个或多个神经元,神经元是最基本的计算单元。每个神经元由一个线性函数和一个非线性激活函数组成,函数的参数即神经网络需要学习得出的权重。
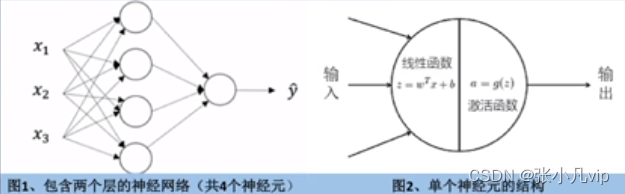
如果不使用非线性激活函数,那么每一个神经元都是线性的,多个神经元的线性组合仍然是线性的,最终的输出也是线性拟合,导致神经网络无法拟合非线性的问题。
理解神经网络的核心组件——层(Layer)
神经网络的核心组件是层(Layer) ,它是一种数据处理模块,可以将它看成数据过滤器。具体来说,层从输入数据中提取特定的数据表示,将多个简单的层链接起来,可以实现渐进式的数据蒸馏(data distillation) 。深度神经网络模型就像是数据处理的“筛子”——包含一系列越来越精细的数据过滤器(即层),最终得到给定数据到目标(LabeL)之间的映射规则。

举例来说:
在一个人脸识别模型中,我们建立了包含4层的神经网络。逐层提取输入图像的特征,每一层都会继续处理已被前面的层处理过的数据,提取的特征也越来越抽象,
如图:

第1层:开始识别明/暗像素
第2层:识别边缘和形状
第3层:学习到更为复杂的形状和睑部单元
第4层:学习人脸由哪些单元定义
这些层链接在一起形成一个数学框架,最终建立人脸图片与姓名的映射规则。
理解权重(weight)的概念及作用
神经网络中每层对输入数据所做的具体操作保存在该层的权重(weight)中,其本质是一串数字。每一层实现的变换由其权重来数化,权重也被称为每一层的参数(parameter) 。
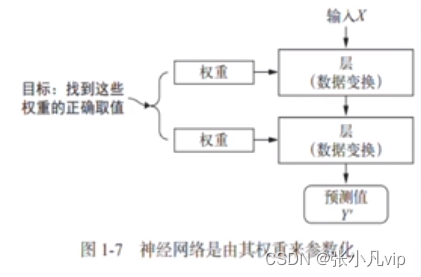
学习(训练)的目的就是为神经网络的所有层都找到一组权重值,使得该网络能够将每个数据输入与其目标正确他对应(即建立映射规则)。一个神经网络可能包含数干万个参数,找到所有数的正确取值可能是一项非常艰巨的任务,往往需要强大的硬件、优秀的深度学习算法及框架支持。
从数学意义上说,深度学习(神经网络)本质上是一个求解权重参数的过程,从而定义出输入和目标的映射规则。
理解损失函数(Loss function)的作用
损失函数(Loss function)也叫目标函数、误差函数,其作用是衡量当前输出值与预期值之间的距离(即损失值、误差值),从而衡量出当前神经网络的好坏。
图-损失函数用来衡量网络输出结果的质量
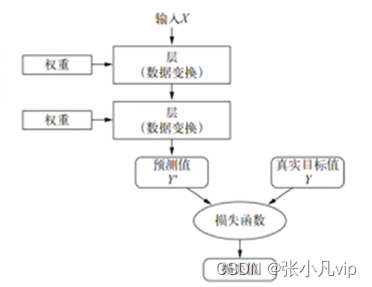
深度学习会依据这个距离值作为反馈信号来调整网络中每一层的权重参数,以降低损失值,(而得出更准确的模型(即输入数据和目标之间的映射)。
理解优化器(Optimizer)的作用
深度学习的基本技巧就是利用损失函数的误差值作为反馈来对权重进行微调,以降低当前示的损失值。这种调节由优化器(optimizer)完成,它实现了所谓的反向传播(backpropagation)算法,这是深度学习的核心算法。
图-将损失值作为反馈信号来调节权重
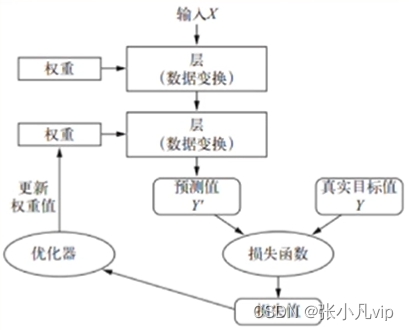
网络各层的权重是随机初始化的,其初始输出值和目标值相去甚远,即损失值很高,但随着训练的迭代,网络处理的数据样本越来越多,权重值也会向正确的方向逐步微调,损失值逐渐降低。当训练次数足够多时,最终得到的权重值就司以使损失函数最小,输出值与目标值尽可能他接近,从而得到训练好的网络。
权重参数、损失函数、优化器及反向传播算法共同形成了神经网络的工作原理,本质上是一个数学框架。
理解神经网络的学习方式——反向传播算法
神经网络的学习过程是对各层权重参数的迭代优化,属于监督学习范畴。权重的修改基于网络在训练集上的表现,训练集中样本所属的分类是已知的。学习的目标是最小化损失函数。
反向传播是神经网络的核心算法,该算法的基本步骤如下所示:
第一步:以随机权重初始化神经网络。
第二步:对于每个训练样本,重复以下过程:
●前向传播:使用误差函数计算网络产生的总误差,即网络的输出与正确输出的差值。
●反向传播:从输出层到输入层,反向遍历所有层。
第三步:在反向遍历过程中,根据上一层的误差和对应权值,逐层计算网络内部各层误差,从而将总误差输出层向隐藏层(即中间层)反向传播,直至传擂到输入层。
第四步:根据各层误差调整各层的权重,以最小化损失函数(即误差函数)。
理解神经网络的学习方式——权重优化(梯度下降)
优化器是如何最小化损失函数的呢?(即如何优化神经网络各层的权重),最常用的算法是赫度下降法(Gradient Descent,GD)。梯度即曲面上一个点沿着给定方向的倾斜程度,数学上是一个偏导数。
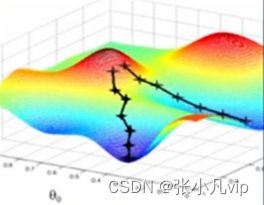
该算法的具体步骤如下所示:
(1)随机选择参数初始值;
(2)对模型中的每个参数,计算误差函数的梯度G;
(3)调整模型参数,使其向误差减小的方向,即G方向移动;
(4)重复步骤2和3,直到G的值趋于0。
梯度下降方法一个形象的比喻是:走哪条路能更快到达山底(即最低位置,相当于损失函数的最小值)
了解常见的神经网络架构
神经网络的架构是由节点间的连接方式、网络的层数(即输入层与输出层之间的节点层数)和每层的神经元数量决定的。神经网络的架构有很多种,常用的有三大类——多层感知机(前馈神经网络)、卷积神经网络(CNN)与循环神经网络(RNN)。
多层感知机(前馈神经网络)
1.每个神经元与下一层的所有神经元均相连
2.同一层的神经元之间均不相连
3.不相邻的层中的神经元之间没有联系
4.网络的层数和每层中神经元的数量取决于需要解决的问题
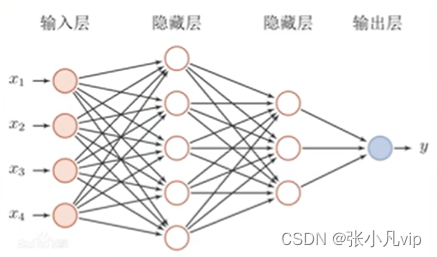
前馈神经网络是应用最广泛的神经网络,卷积神经网络(CNN)就是一种经典的前馈神经网络。
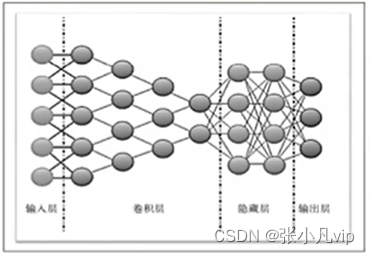
卷积神经网络与循环神经网络
卷积神经网络(CNN)针对图像识别任务,引入卷积层,使用卷积核【矩阵】对数据逛行卷积操作,得到多个特征映射。
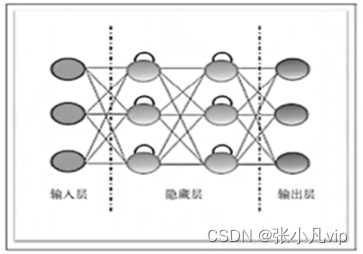
循环神经网络(RNN)的神经元包含反馈连接,能够处理与时间序列相关的任务,在自然语言处理(NLP)应用广泛,如语音识别、语言建模、机器翻译等。
总结
神经网络本质上是一个实现深度学习的多层数学框架,每一层都对输入数据做一定的转换,在训练(学习)的过程中不断调整优化各层的权重参数,最终得到能够准确映射输入数据和目标输出的网络模型。
优化器的作用是依据误差值来逐步调整各层的权重然数,以降低误差值。这一过程的算法叫做反向传播(Backpropagation )算法,梯度下降(GD)是反向传播算法中常用的方法。
通过在大量数据上多次循环训练,最终可以得到最小化的损失函数,从而得出训练好的神经网络(即能够准确映射输入数据和目标输出的深度学习模型)。
神经网络各层的权重参数在初始化时是随机赋值的,训练过程就是不断优化权重的过程。
卷积神经网络和循环神经网络是当前应用最广泛两种神经网络结构。
权重参数、损失函数、优化器及反向传播算法共同形成了神经网络的工作原理,本质上是一个数学框架。