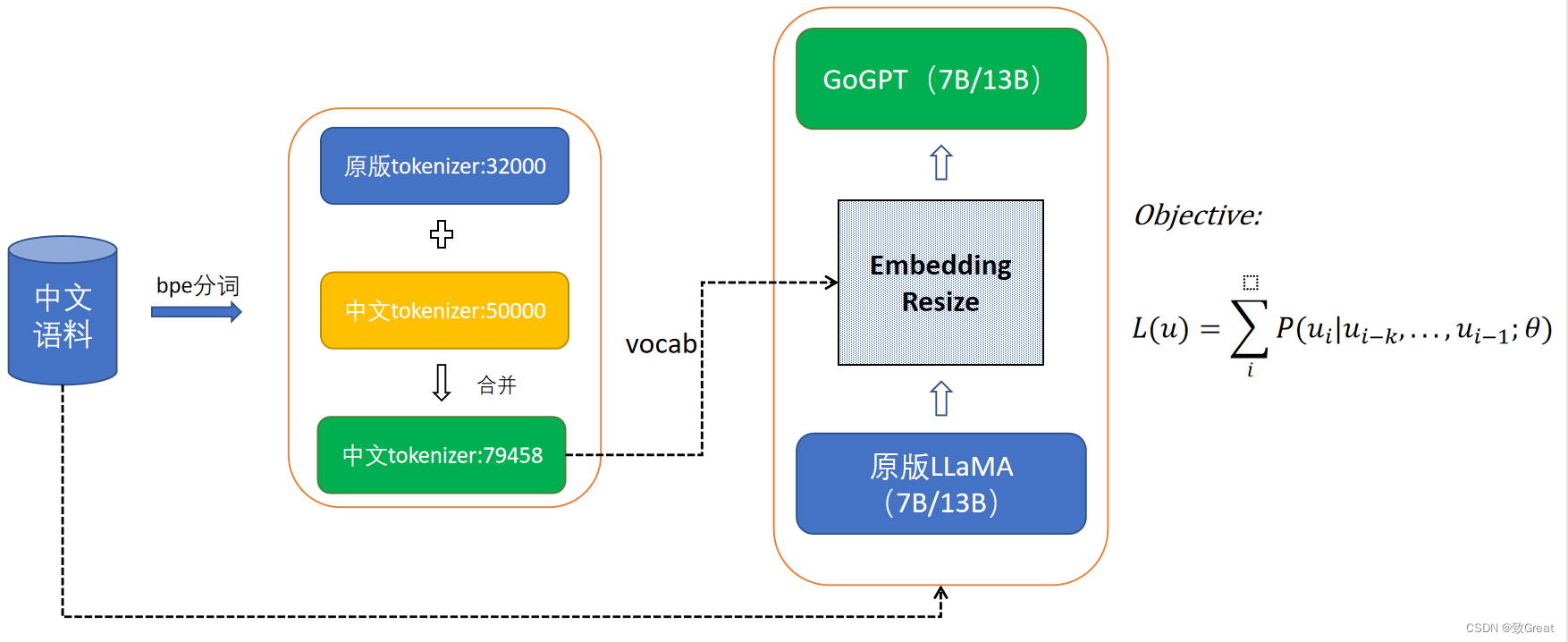
第1关：单纯性算法解一般线性方程组

任务描述

本关任务：编写一个利用两阶段单纯性算法求一般线性规划的程序。

相关知识

单纯形算法的第1步：选出使目标函数增加的非基本变量作为入基变量。

查看单纯形表的第 1 行（也称之为z行）中标有非基本变量的各列中的值。 选出使目标函数增加的非基本变量作为入基变量。

单纯形算法的第2步：选取离基变量。

在单纯形表中考察由第 1 步选出的入基变量所相应的列。 在一个基本变量变为负值之前，入基变量可以增到多大。 如果入基变量所在的列与基本变量所在行交叉处的表元素为负数，那么该元素将不受任何限制，相应的基本变量只会越变越大。 如果入基变量所在列的所有元素都是负值，则目标函数无界，已经得到了问题的无界解。 如果选出的列中有一个或多个元素为正数，要弄清是哪个数限制了入基变量值的增加。 受限的增加量可以用入基变量所在列的元素（称为主元素）来除主元素所在行的“常数列”（最左边的列）中元素而得到。所得到数值越小说明受到限制越多。 应该选取受到限制最多的基本变量作为离基变量，才能保证将入基变量与离基变量互调位置后，仍满足约束条件。

单纯形算法的第3步：转轴变换。

转轴变换的目的是将入基变量与离基变量互调位置。 给入基变量一个增值，使之成为基本变量； 修改离基变量，让入基变量所在列中，离基变量所在行的元素值减为零，而使之成为非基本变量。

单纯形算法的第4步：转回并重复第1步，进一步改进目标函数值。

不断重复上述过程，直到z行的所有非基本变量系数都变成负值为止。

编程要求

根据提示，在右侧编辑器补充代码。

测试说明

平台会对你编写的代码进行测试：

测试输入：

1. 1 //1：(max) -1(min)
2. 4 4 // 不等式个数m=4, 变量个数n=4
3. 2 1 1 // m1(≤)=2, m2(=)=1,m3(≥)=1
4. 1 0 2 0 18 //x1 + 2x3 ≤ 18
5. 0 2 0 -7 0// 2x2 - 7x4 ≤ 0
6. 1 1 1 1 9 // x1+x2+x3+x4 = 9
7. 0 1 -1 2 1//x2-x3x+2x4 ≥1
8. 1 1 3 -1 //目标函数 z = x1+x2+3x3-x4

---

开始你的任务吧，祝你成功！

参考答案：

#pragma once
#include <cmath>
#include <iostream>
#include<fstream>
#include <string>
#include <iomanip>
#include <cfloat>
using namespace std;
class LinearProgram
{
            
public:
        LinearProgram();
        ~LinearProgram();
        void solve();
    private:
        int enter(int objrow);
        int leave(int col);
        int simplex(int objrow);
        int phase1();
        int phase2();
        int compute();
        void swapbasic(int row,int col);
        void pivot(int row,int col);
    //    void stats();//这个方法是干什么的？
        void setbasic(int * basicp);
        void output();
        void Make2DArray(double ** & a, int m,int n);
        void Delet2DArray(double ** & a, int m,int n);
        int m,                //约束总数
            n,                //变量数
            m1,                //不等式约束数<=
            m2,                //等式约束
            m3,                //不等式约束数>=
            n1,n2,            //n1 = n + m3,n2 = n1 + m1
            error,            //记录错误类型
            *basic,            //基本变量下标
            *nonbasic;        //非基本变量下标
        double **a,minmax;
};
LinearProgram::LinearProgram()
{
            
    double value;
    cout<<"Enter data in the following format:"<<endl;
    cout<<"1:+1(max)or-1(min);m;n"<<endl;
    cout<<"2:m1;m2;m3"<<endl;
    cout<<"The constraint coefficient and the right term"<<endl;
    cout<<"Objective function coefficient"<<endl;
    error = 0;
    cin>>minmax;
    cin>>m;
    cin>>n;
    //输入各类约束数
    cin>>m1;
    cin>>m2;
    cin>>m3;
    if(m!=m1+m2+m3)
    {
            
        error = 1;
    }
    n1 = n + m3;
    n2 = n + m1 + m3;
    Make2DArray(a,m+2,n1+1);//构造二维数组
    basic = new int[m+2];
    nonbasic = new int[n1+1];
    //初始化基本变量和非基本变量
    /*********begin*************/
        for(int i=0; i<=m+1; i++)
    {
            
        for(int j=0; j<=n1; j++)
        {
            
            a[i][j] = 0.0;
        }
    }
    for(int j=0; j<=n1; j++)
    {
            
        nonbasic[j] = j;
    }
    /*********end***************/
    //引入松弛变量和人工变量
    /*********begin*************/
        for(int i=1,j=n1+1; i<=m; i++,j++)
    {
            
        basic[i] = j;
    }
    for(int i=m-m3+1,j=n+1; i<=m; i++,j++)
    {
            
        a[i][j] = -1.0;
        a[m+1][j] = -1.0;
    }
    /*********end***************/
    //输入约束系数和右端项
    for(int i=1; i<=m; i++)
    {
            
        for(int j=1; j<=n; j++)
        {
            
            cin>>value;
            a[i][j] = value;
        }
        cin>>value;
        if(value<0) 
        {
            
            error = 1;
        }
        a[i][0] = value;
    }
    //输入目标函数系数
    for(int j=1; j<=n; j++)
    {
            
        cin>>value;
        a[0][j] =  value * minmax;
    }
    //引入人工变量，构造第1阶段的辅助目标函数
    /*********begin*************/
        for(int j=1; j<=n;  j++)
    {
            
        value=0.0;
        for(int i=m1+1; i<=m; i++)
        {
            
            value += a[i][j];
        }
        a[m+1][j] = value;
    } 
    /*********end***************/
}
LinearProgram::~LinearProgram()
{
            
    delete basic;
    delete nonbasic;
    Delet2DArray(a,m+2,n1+1);
}
void LinearProgram::Make2DArray(double ** & a, int m,int n)
{
            
    a = new double*[m];
    for (int i=0; i<m; i++)
    {
            
        a[i] = new double[n];
    }
}
void LinearProgram::Delet2DArray(double ** & a, int m,int n)
{
            
    for (int i = 0; i <= m;i++)
    {
            
        delete[]a[i];
    }
    delete[]a;
}
//根据目标函数系数所在的行objrow，执行约束标准型线性规划问题的单纯形算法
int LinearProgram::simplex(int objrow)
{
            
    /*********begin*************/
        for(int row = 0;;)
    {
            
        int col = enter(objrow);
        if(col>0)
        {
            
            row = leave(col);
        }
        else
        {
            
            return 0;
        }
        if(row>0)
        {
            
            pivot(row,col);
        }
        else
        {
            
            return 2;
        }
    }
    /*********end***************/
}
//根据目标函数系数所在行objrow，选取入基变量
int LinearProgram::enter(int objrow)
{
            
    double temp = DBL_EPSILON;    
    int j,col;
    /*********begin*************/
    for(j=1,col=0; j<=n1; j++)
    {
            
        if(nonbasic[j]<=n2 && a[objrow][j]>temp)
        {
            
            col = j;
            temp = a[objrow][j];
            break;            //Bland避免循环法则
        }
    }
    /*********end***************/
    return col;
}
//根据入基变量所在列col,选取离基变量
int LinearProgram::leave(int col)
{
            
    double temp = DBL_MAX;
    int row, i;
    /*********begin*************/
        for(i=1,row=0; i<=m; i++)
    {
            
        double val = a[i][col];
        if(val>DBL_EPSILON)
        {
            
            val = a[i][0]/val;
            if(val<temp)
            {
            
                row = i;
                temp = val;
            }
        }
    }
    /*********end***************/
    return row;
}
//以入基变量所在列col和离基变量所在行row交叉处元素a[row][col]为轴心，做转轴变换
void LinearProgram::pivot(int row,int col)
{
            
    /*********begin*************/
    for(int j=0; j<=n1; j++)
    {
            
        if(j!=col)
        {
            
            a[row][j] = a[row][j]/a[row][col];
        }
    }
    a[row][col] = 1.0/a[row][col];
    for(int i=0; i<=m+1; i++)
    {
            
        if(i!=row)
        {
            
            for(int j=0; j<=n1; j++)
            {
            
                if(j!=col)
                {
            
                    a[i][j] = a[i][j] - a[i][col]*a[row][j];
                    if(fabs(a[i][j])<DBL_EPSILON)
                    {
            
                        a[i][j] = 0.0;
                    }
                }
            }
            a[i][col] = - a[i][col]*a[row][col];
        }
    }
    /*********end***************/
    swapbasic(row,col);
}
//交换基本变量row和非基本变量col的位置
void LinearProgram::swapbasic(int row,int col)
{
            
    int temp = basic[row];
    basic[row] = nonbasic[col];
    nonbasic[col] = temp;
}
//对一般的线性规划问题执行两阶段单纯形算法
int LinearProgram::compute()
{
            
    if(error>0)
    {
            
        return error;
    }
    if(m!=m1)
    {
            
        error = phase1();
        if(error>0)
        {
            
            return error;
        }
    }
    return phase2();
}
//构造初始基本可行解的第一阶段单纯形算法由phase1()实现
//辅助目标函数存储在数组a的第trows行
int LinearProgram::phase1()
{
            
    error = simplex(m+1);
    if(error>0)
    {
            
        return error;
    }
    for(int i=1; i<=m; i++)
    {
            
        if(basic[i]>n2)
        {
            
            if(a[i][0]>DBL_EPSILON)
            {
            
                return 3;
            }
            for(int j=1; j<=n1; j++)
            {
            
                if(fabs(double(a[i][j]))>=DBL_EPSILON)
                {
            
                    pivot(i,j);
                    break;
                }    
            }
        }
    }
    return 0;
}
//第二阶段根据第一阶段找到的基本可行解，对原来的目标函数用单纯形算法求解
//原目标函数存储在数组a的第0行
int LinearProgram::phase2()
{
            
    return simplex(0);
}
//执行两阶段单纯形算法
void LinearProgram::solve()
{
            
    cout<<endl<<"* * * 线性规划---单纯形算法 * * *"<<endl<<endl;
    error = compute();
    switch(error)
    {
            
        case 0:output();break;
        case 1:cout<<"输入数据错误--"<<endl;break;
        case 2:cout<<"无界解--"<<endl;break;
        case 3:cout<<"无可行解--"<<endl;
    }
    cout<<"计算结束"<<endl;
}
//输出结果
void LinearProgram::output()
{
            
    int width = 8,*basicp;
    double zero = 0.0;
    basicp = new int[n+m+1];
    setbasic(basicp);
    cout.setf(ios::fixed|ios::showpoint|ios::right);
    cout.precision(4);
    cout<<endl<<"最优值："<<-minmax*a[0][0]<<endl<<endl;
    cout<<"最优解："<<endl<<endl;
    for(int j=1; j<=n; j++)
    {
            
        cout<<"x"<<j<<" =";
        if(basicp[j]!=0)
        {
            
            cout<<setw(width)<<a[basicp[j]][0];
        }
        else
        {
            
            cout<<setw(width)<<zero;
        }
        cout<<endl;
    }
    cout<<endl;
    delete []basicp;
} 
void LinearProgram::setbasic(int * basicp)
{
            
    for(int i=0;i<=n+m;i++)
    {
            
        basicp[i] = 0;
    }
    for(int i=1;i<=m;i++)
    {
            
        basicp[basic[i]]=i;
    }
}

如果对你有所帮助，感谢点赞加收藏！

关于接下来的实验内容，我也会在【WRITE-BUG数字空间】更新，也可以为大家带来更好的观感，带来更多的分享，欢迎大家前来浏览。

算法设计与分析：线性规划问题和单纯形算法（作业-必做）(头歌实验） -文章频道 - 我的学习圈 - 个人学习圈 (writebug.com)https://www.writebug.com/article/f5406a00-f3e5-11ed-93f4-0242ac14000d