1. 哎呀，不小心把不能提交的“机密”加入commit了

• 按快捷键alt+9打开git窗口
• 可以看到刚误提交的commit，还好还没push到远程库，还有的救
  

2. 使用reset来修复的话要注意有坑，选Soft和Mixed，千万别选Hard和Keep

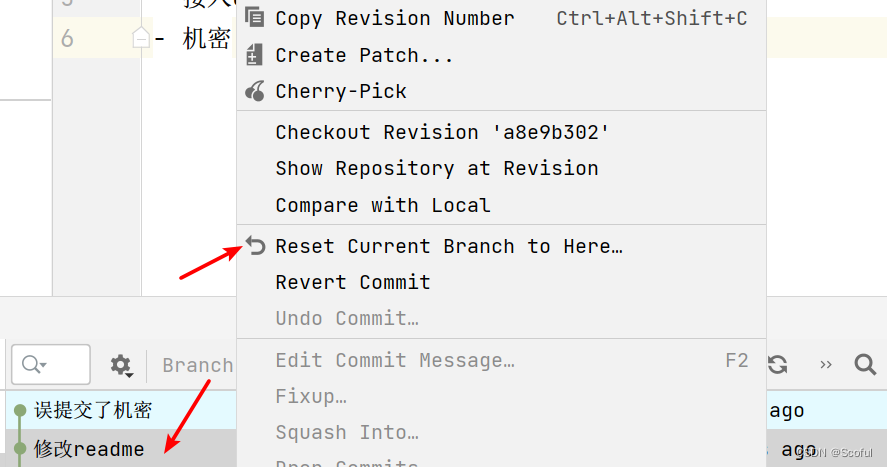
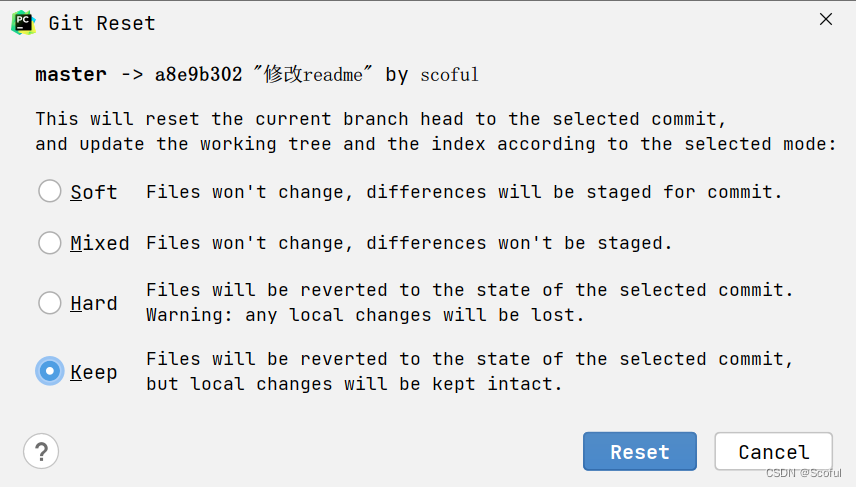
• 右键选中前一个commit，选reset
• 可以看到有4种选择，其中Soft和Mixed都可以在撤销commit的前提下还会留下文件的修改
• 但是，Hard和Keep，会撤销commit，但是会把所有文件的修改都去掉，辛辛苦苦写的代码一下子就没了

3. 使用revert，只能修修补补，但commit还在，当然有好处是会留下使用痕迹，方便别人理解

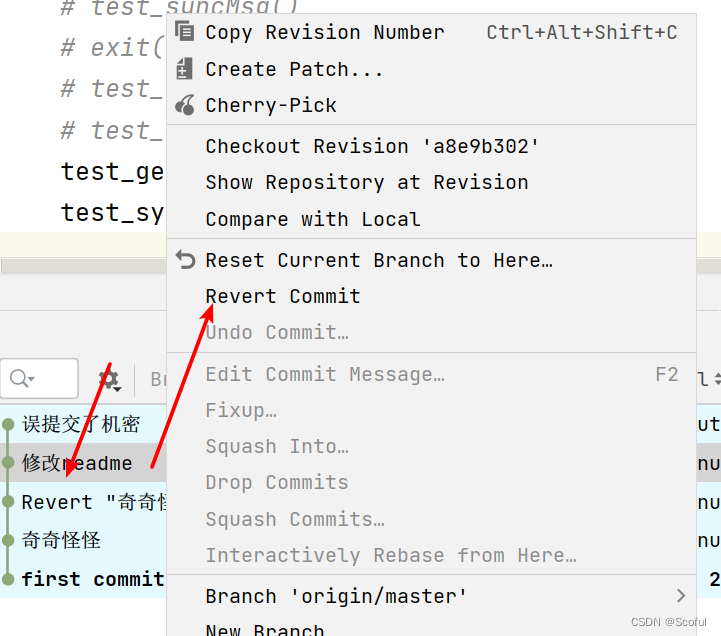
4. 推荐使用：undo commit

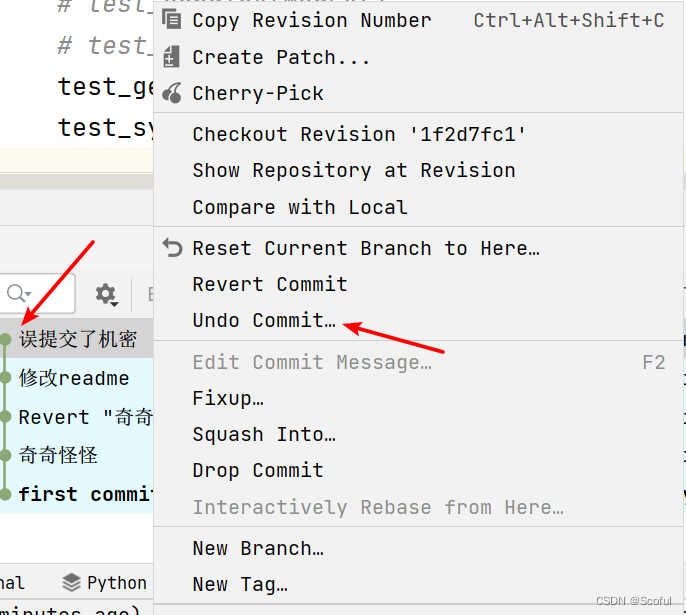
• 简单方便，一键搞定，还不用纠结用哪一个模式，Soft，Mixed，Hard，Keep，其实看命令就是Soft模式

5. reset和revert的区别

• 大白话说就是，reset会直接掩盖痕迹，别人不知道你犯过蠢
• 而revert就是给你改过的机会，但是会留下黑历史，别人一看就知道曾经犯过蠢，好处就是有助于别人理解思路过程

enjoy！