目录
- 1. fft和ifft的原理
- 1.1 fft
- 1.2 ifft
- 2. 书写代码思路
- 3. 完整代码
- 4. 结果图
1. fft和ifft的原理
1.1 fft
fft是快速傅里叶变换,是MATLAB中计算信号频谱的函数,使用方法是fft(x),直接对信号x进行fft计算。
由于fft函数计算信号的频谱是0-fs范围的,但是我们更习惯观察的信号的双边频谱,即-fs/2-fs/2范围的频谱,因此常用fftshift(x)函数将0-fs范围的信号频谱搬移到-fs/2-fs/2范围,也就是将原来0-fs范围中的fs/2-fs范围的频谱搬移到-fs/2-0范围处。
1.2 ifft
ifft是快速逆傅里叶变换,是MATLAB中求信号的逆傅里叶变换的函数,使用方法是ifft(x)。
2. 书写代码思路
1.养成良好习惯,在代码的最上面书写三件套代码,该清除的清除。
clear all; % 清除所有变量
close all; % 关闭所有窗口
clc; % 清屏
2.确定各个信号的频率以及信号的最高频率,本例中信号是正弦信号和余弦信号之和,分别确定各个信号频率,以及信号的最高频率,这里是3000Hz
fc1 = 1000; % 信号1的中心频率
fc2 = 3000; % 信号2的中心频率
3.根据信号的最高频率和奈奎斯特采样定理确定采样频率(大于信号最高频率的2倍即可),本人为了时域信号的平滑,通常将采样频率设置为最高频率的30倍左右。
fs = 100000; % 采样频率,满足奈奎斯特采样定理即可,这里为信号频率的33倍原因是为了采样点数多,时域波形平滑
4.根据采样频率求得采样间隔,即采样频率的倒数
dt = 1/fs; % 采样间隔
5.确定仿真信号时长,这个一般根据实际情况来定,例如在通信系统中,首先需要确定码元周期,然后确定码元个数,两者相乘即是仿真时长,在本例中设置的时长是0.1。
T = 0.1; % 采样总时长
6.确定采样点数,为采样时长除以采样间隔。
N = T*fs; % 采样点数,N=T/dt=T*fs
7.确定仿真时间变量,从0开始,以采样间隔为间隔,形成1*N的行向量
t = 0:dt:(N-1)*dt; % 时间行向量,间隔为dt
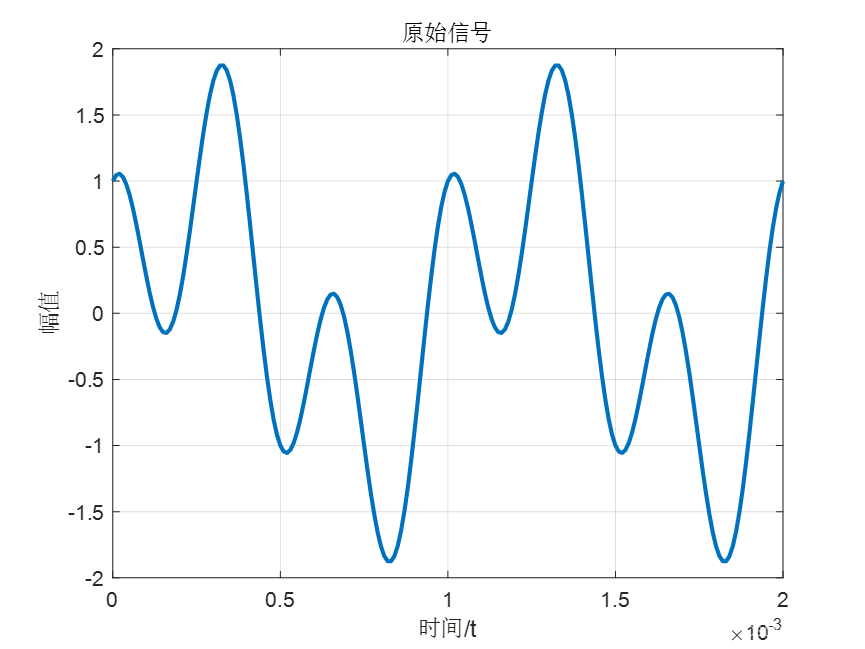
8.产生信号,并且绘制图像。
sig = sin(2*pi*fc1*t)+cos(2*pi*fc2*t);% 信号
figure(1); % 绘制第1幅图
plot(t,sig,'LineWidth',2); % 绘制信号波形
axis([0 0.002 -2 2]); % 坐标轴范围设置
xlabel('时间/t'); % 横坐标标签
ylabel('幅值'); % 纵坐标
title('原始信号'); % 标题
grid on; % 打开网格线
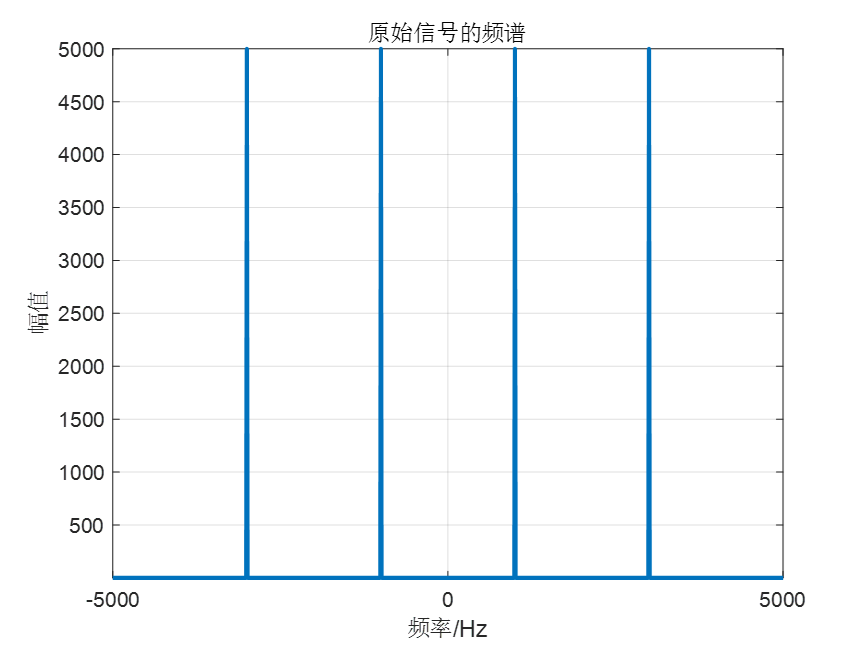
9.对信号进行fft,fft三步走
sig_f = fft(sig); % 对信号进行fft
sig_f_2 = abs(sig_f); % fft后取绝对值得到幅度响应
sig_f_2 = fftshift(sig_f_2);% 将0-fs频谱移动到-fs/2-fs/2
10.确定频谱分辨率fs/N=1/T
df = 1/T; % 频谱分辨率fs/N=1/T
11.确定频谱范围,即-fs/2-fs/2,间隔为频谱分辨率
f=(-N/2:N/2-1)*df; % 频率范围
12.绘制频谱
figure(2); % 绘制第2幅图
plot(f,sig_f_2,'LineWidth',2);% 绘制信号的频谱
axis([-5000 5000 -inf inf]);% 坐标轴范围设置
xlabel('频率/Hz'); % 横坐标标签
ylabel('幅值'); % 纵坐标
title('原始信号的频谱'); % 标题
grid on; % 打开网格线
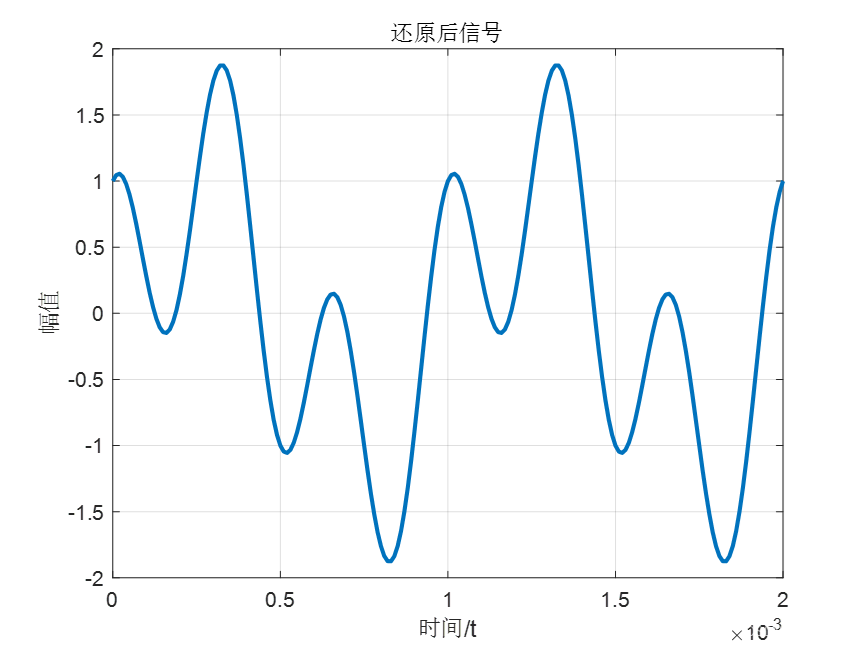
13.对信号做ifft,这里是对fft后的信号sig_f进行ifft,而不是对进行fft三步走后的信号sig_f_2进行ifftshift,然后进行ifft,因为三步走中有一步是取绝对值,通过ifftshift然后ifft无法准确还原出原始信号,因此为了还原出原始信号,应该对fft后的信号sig_f进行ifft,这也是为什么要三步走的原因,而不采用一行生成的代码fftshift(abs(fft(x)))。
sig_ifft = ifft(sig_f); % 对fft后的信号进行ifft还原成时域信号
14.绘制还原后信号图像
plot(t,sig_ifft,'LineWidth',2);% 绘制还原后的时域信号
axis([0 0.002 -2 2]); % 坐标轴范围设置
xlabel('时间/t'); % 横坐标标签
ylabel('幅值'); % 纵坐标
title('还原后信号'); % 标题
grid on; % 打开网格线
3. 完整代码
clear all; % 清除所有变量
close all; % 关闭所有窗口
clc; % 清屏
%% 基本参数
fc1 = 1000; % 信号1的中心频率
fc2 = 3000; % 信号2的中心频率
fs = 100000; % 采样频率,满足奈奎斯特采样定理即可,这里为信号频率的33倍原因是为了采样点数多,时域波形平滑
dt = 1/fs; % 采样间隔
T = 0.1; % 采样总时长
N = T*fs; % 采样点数,N=T/dt=T*fs
t = 0:dt:(N-1)*dt; % 时间行向量,间隔为dt
sig = sin(2*pi*fc1*t)+cos(2*pi*fc2*t);% 信号
figure(1); % 绘制第1幅图
plot(t,sig,'LineWidth',2); % 绘制信号波形
axis([0 0.002 -2 2]); % 坐标轴范围设置
xlabel('时间/t'); % 横坐标标签
ylabel('幅值'); % 纵坐标
title('原始信号'); % 标题
grid on; % 打开网格线
sig_f = fft(sig); % 对信号进行fft
sig_f_2 = abs(sig_f); % fft后取绝对值得到幅度响应
sig_f_2 = fftshift(sig_f_2);% 将0-fs频谱移动到-fs/2-fs/2
df = 1/T; % 频谱分辨率fs/N=1/T
f=(-N/2:N/2-1)*df; % 频率范围
figure(2); % 绘制第2幅图
plot(f,sig_f_2,'LineWidth',2);% 绘制信号的频谱
axis([-5000 5000 -inf inf]);% 坐标轴范围设置
xlabel('频率/Hz'); % 横坐标标签
ylabel('幅值'); % 纵坐标
title('原始信号的频谱'); % 标题
grid on; % 打开网格线
sig_ifft = ifft(sig_f); % 对fft后的信号进行ifft还原成时域信号
figure(3); % 绘制第3幅图
plot(t,sig_ifft,'LineWidth',2);% 绘制还原后的时域信号
axis([0 0.002 -2 2]); % 坐标轴范围设置
xlabel('时间/t'); % 横坐标标签
ylabel('幅值'); % 纵坐标
title('还原后信号'); % 标题
grid on; % 打开网格线
4. 结果图