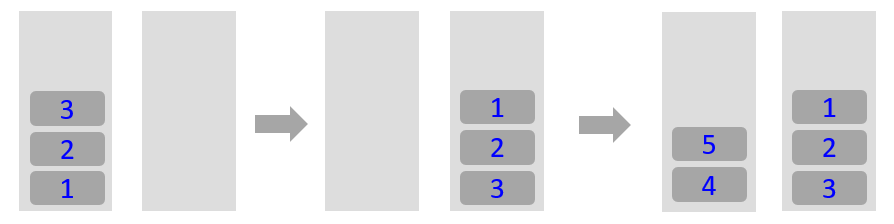
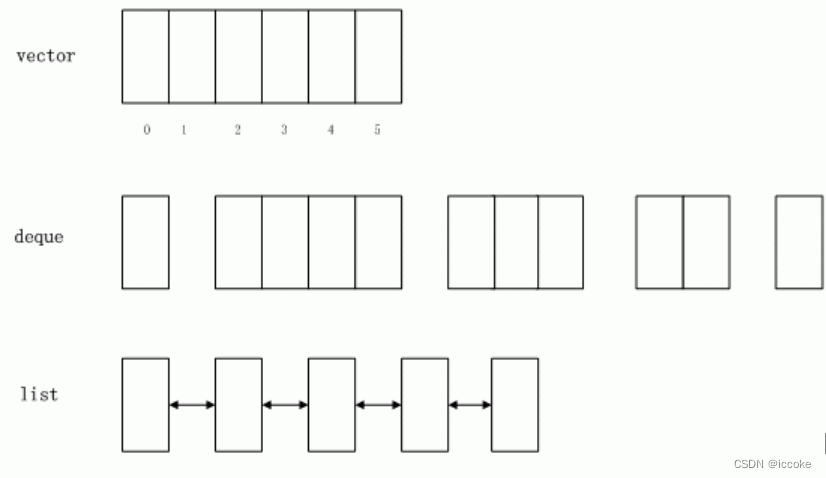
栈(stack)是一种用于存储数据的简单数据结构。栈一个有序线性表,只能在表的一端(PS:栈顶)执行插人和删除操作。最后插人的元素将被第一个删除。所以,栈也称为后进先出(Last In First Out,LIFO)或先进后出(First In Last Out,FILO)线性表。
栈的几种常用方法。
public interface Stack<E> extends Iterable<E> {
//获取栈的size大小
public int size();
//判断栈是否为空
public boolean isEmpty();
//入栈 进栈一个元素 在线性表的表尾添加一个元素
public void push(E element);
//出栈 弹出一个元素 在线性表的表尾删除一个元素
public E pop();
//查看当前栈顶元素 并不是移除 查看线性表中最后一个元素
public E peek();
//对当前栈进行清空
public void clear();
}练习题:
20 有效的括号
给定一个只包括 '(',')','{','}','[',']' 的字符串 s ,判断字符串是否有效。
解题1:
很明显的一种栈的使用。每次入栈的时候,判断当前元素和栈顶元素是否配对,如果配对,则弹出,如果不配对,则继续入栈。最后栈元素为空,则true,否则,为false。
class Solution {
public boolean isValid(String s) {
Stack<Character> stack = new Stack<>();
for (int i = 0; i < s.length(); i++) {
if (stack.size() == 0 || !isPair(stack.peek(), s.charAt(i))) {
stack.push(s.charAt(i));
} else {
stack.pop();
}
}
return stack.size() == 0;
}
public static boolean isPair(char x, char y) {
if (x == '(' && y == ')') {
return true;
}
if (x == '[' && y == ']') {
return true;
}
if (x == '{' && y == '}') {
return true;
}
return false;
}
}解题2:
遇到左括号,则对应的右括号入栈,遇到右括号,则比较与栈顶元素是否一致,一致则出栈,继续,否则直接返回false。
class Solution {
public boolean isValid(String s) {
Stack<Character> stack = new Stack<>();
for (int i = 0; i < s.length(); i++) {
char c = s.charAt(i);
if (c == '(') {
stack.push(')');
} else if (c == '[') {
stack.push(']');
} else if (c == '{') {
stack.push('}');
} else {
if (!stack.isEmpty() && s.charAt(i) == stack.peek()) {
stack.pop();
} else {
return false;
}
}
}
return stack.isEmpty();
}
}150 后缀表达式,逆波兰表达式求值。
给你一个字符串数组 tokens ,表示一个根据 逆波兰表示法 表示的算术表达式。
public int evalRPN1(String[] tokens) {
Stack<Integer> stack = new Stack<>();
for (String token : tokens) {
if ("+".equals(token)) {
Integer b = stack.pop();
Integer a = stack.pop();
stack.push(a + b);
} else if ("-".equals(token)) {
Integer b = stack.pop();
Integer a = stack.pop();
stack.push(a - b);
} else if ("*".equals(token)) {
Integer b = stack.pop();
Integer a = stack.pop();
stack.push(a * b);
} else if ("/".equals(token)) {
Integer b = stack.pop();
Integer a = stack.pop();
stack.push(a / b);
} else {
stack.push(Integer.parseInt(token));
}
}
return stack.peek();
}中缀表达式转后缀表达式:
1、简单版本,没有括号,只有加减乘除
解题思路:
- 定义一个栈,用于存放运算符
- 定义一个新数组,长度和给定的中缀表达式数组长度一样,然后遍历给定的数组
- 如果遇到的不是运算符,那么直接存在新数组中
- 如果栈为空,或者栈顶的运算符优先级小于当前运算符优先级,那么当前运算符入栈(例如,当前栈顶为+,如果遇到*,那么就直接将*入栈)
- 如果运算符优先级大于等于当前运算符优先级,那么弹出栈顶元素,存入新数组中,然后循环这一步骤
- 跳出5的循环后,将当前运算符入栈。
- 遍历完成后,对当前栈进行操作,不断将栈顶元素弹出,添加到新数组中。
public static String[] Infix2Suffix(String[] tokens) {
Stack<String> stack = new Stack<>();
String[] res = new String[tokens.length];
int count = 0;
for (String token : tokens) {
int fix = fix(token);
if (fix == 0) {
res[count++] = token;
} else if (stack.isEmpty() || fix > fix(stack.peek())) {
stack.push(token);
} else {
while (!stack.isEmpty() && fix <= fix(stack.peek())) {
String pop = stack.pop();
res[count++] = pop;
}
stack.push(token);
}
}
while (!stack.isEmpty()) {
res[count++] = stack.pop();
}
return res;
}
public static int fix(String str) {
if ("+".equals(str) || "-".equals(str)) {
return 1;
} else if ("*".equals(str) || "/".equals(str)) {
return 2;
} else {
return 0;
}
}2、升级版本,带括号
解题思路:
和上述不带括号的差不多,区别就是:
- 遇到左括号,直接入栈
- 遇到右括号,把左括号之前的运算符全部出栈,添加到新数组里面,直到遇到左括号,把左括号弹出丢弃
/**
* 中缀转后缀,带括号版本
*/
public static String[] Infix2Suffix1(String[] tokens) {
Stack<String> stack = new Stack<>();
String[] res = new String[tokens.length];
int count = 0;
for (String token : tokens) {
int fix = fix(token);
if (fix == 0) {
if (token.equals("(")) {
stack.push(token);
} else if (token.equals(")")) {
while (!stack.isEmpty() && !stack.peek().equals("(")) {
String pop = stack.pop();
res[count++] = pop;
}
if (!stack.isEmpty()) {
stack.pop();
}
} else {
res[count++] = token;
}
} else if (stack.isEmpty() || fix > fix(stack.peek())) {
stack.push(token);
} else {
while (!stack.isEmpty() && fix <= fix(stack.peek())) {
String pop = stack.pop();
res[count++] = pop;
}
stack.push(token);
}
}
while (!stack.isEmpty()) {
res[count++] = stack.pop();
}
return res;
}232. 用栈实现队列
请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作(push、pop、peek、empty)
解题思路:
- 题目要求用两个栈实现队列的操作,即先入先出
- 定义两个栈,一个栈1专门用于存储数据,执行push操作,一个栈2用来执行出队列操作,执行pop和peek操作。
- 栈1,只负责执行push,如果遇到添加操作,就把值push到栈1中即可。
- 出队列的时候,考虑需要把最初添加进入的元素给弹出来,一个栈显然执行不了这个操作,因此栈2 作为辅助栈,执行出栈前,先把栈1中所有的元素逐个弹出来,添加到栈2中,这样就相当于把栈1中的元素顺序调换了,此时,栈2顶部的元素,就是最初添加的元素,可以直接pop出来。
- 后续执行操作时,栈2只要不为空,那么栈顶的元素就是当前元素中,最先添加的元素,直接pop就好。
- 判空:两个栈都为空,队列才为空。
图示,先push1,2,3,然后peek,栈1内元素转到栈2,后面只要栈2不为null,就可以执行pop和peek操作,如果为空,在吧元素从栈1转到栈2 就可以了。
class MyQueue {
Stack<Integer> stack;
Stack<Integer> reStack;
public MyQueue() {
stack = new Stack<>();
reStack = new Stack<>();
}
public void push(int x) {
stack.push(x);
}
public int pop() {
if (reStack.isEmpty()) {
while (!stack.isEmpty()) {
reStack.push(stack.pop());
}
}
return reStack.pop();
}
public int peek() {
if (reStack.isEmpty()) {
while (!stack.isEmpty()) {
reStack.push(stack.pop());
}
}
return reStack.peek();
}
public boolean empty() {
return reStack.isEmpty() && stack.isEmpty();
}
}225. 用队列实现栈
请你仅使用两个队列实现一个后入先出(LIFO)的栈,并支持普通栈的全部四种操作(push、top、pop 和 empty)。实现 MyStack 类;
解题思路:
其实和上面的解题思路差不多,两个队列模拟栈的操作,就是将先入先出改成后入先出
- 定义两个栈,q1,q2。
- 添加元素时,先把元素放在q2中,然后,把q1里面的元素全部转移到q2中,这时,最新添加的元素在q2中相当于最一开始添加的元素了,因此可以实现后入先出。
- 此时在交换q1和q2的指针。保证所有元素都在q1里面。每次取元素,从q1取即可。
如图,先添加1,后添加2
public class MyStack {
Queue<Integer> queue1;
Queue<Integer> queue2;
Queue<Integer> temp;
public MyStack() {
queue1 = new ArrayDeque<>();
queue2 = new ArrayDeque<>();
}
public void push(int x) {
queue2.offer(x);
while (!queue1.isEmpty()) {
queue2.offer(queue1.poll());
}
temp = queue1;
queue1 = queue2;
queue2 = temp;
}
public int pop() {
return queue1.poll();
}
public int top() {
return queue1.peek();
}
public boolean empty() {
return queue1.isEmpty() && queue2.isEmpty();
}
}
解题思路2:
上述用两个队列实现了栈的后入先出(两个队列做数据转移),其实一个队列就可以完成:
- 定义一个队列,和一个计数器,计算器用于计算当前队列中元素的个数
- 添加元素时,将新元素添加到队列尾部,然后做一个循环,把这个新元素之前的元素全部poll出来从新添加到这个队列中,那么,新添加的元素就会到队列的头部,这样就可以poll或者peek了
- 怎么解决循环的次数呢?只需要定义一个计数器,记录当前队列中有几个元素就好了。
public class MyStack {
Queue<Integer> queue;
int size;
public MyStack() {
queue = new ArrayDeque<>();
size = 0;
}
public void push(int x) {
queue.offer(x);
for (int i = 0; i < size; i++) {
queue.offer(queue.poll());
}
size++;
}
public int pop() {
size--;
return queue.poll();
}
public int top() {
return queue.peek();
}
public boolean empty() {
return size == 0;
}
}