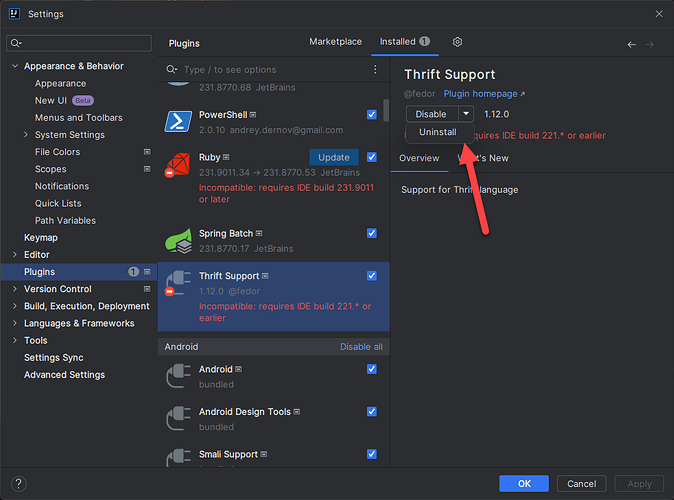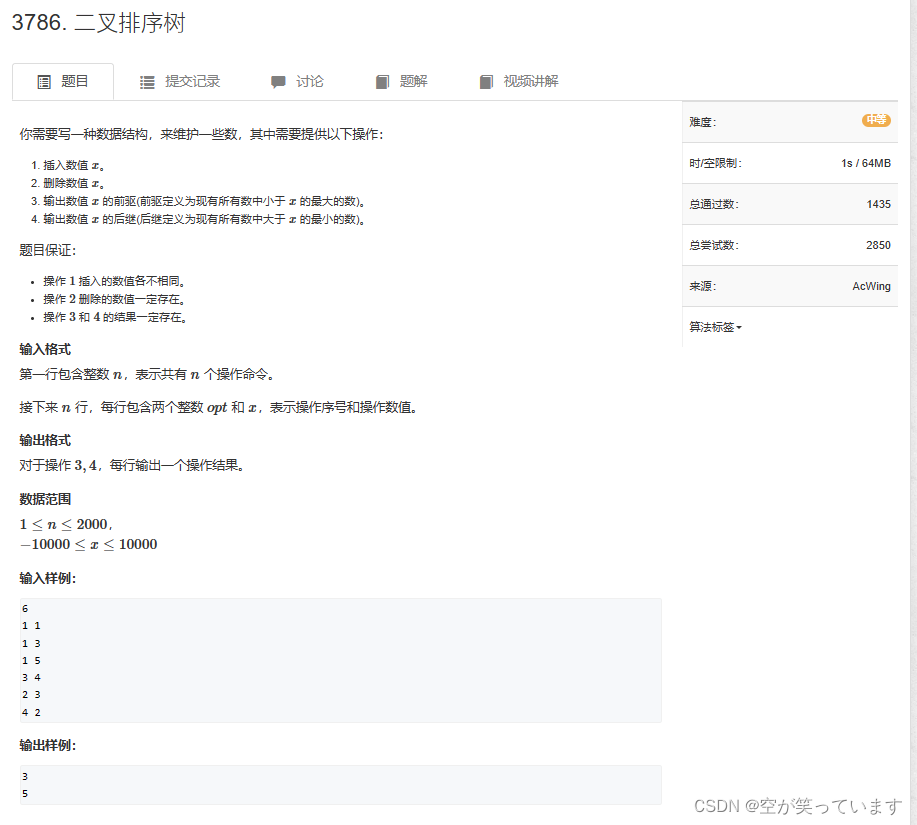
这道题很妙。题目给的二叉排序树好像没学过其实就是二叉查找树。然后这道题主要的就是思路

1.节点的初始化（记住）

struct TreeNode {
     int val;
    TreeNode *left;
     TreeNode *right;
     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};

2.节点的插入

void insert(TreeNode* &root,int x){
    //判断是插入右边还是左边
    if(!root) root = new TreeNode(x);
    if(root->val == x) return;
    if(x > root->val)   insert(root->right,x);
    else if(x < root->val)  insert(root->left,x);
}

 3.节点的删除

    1.先找到那个要删除节点所在处
    2.找到之后处理分三种情况
    删除的节点是叶节点，直接删除即可
    删除的节点只有右节点或者左节点 将左节点或者右节点删除即可
    删除的节点有右结点又有左节点，我们只需要知道Y:中序遍历排在这个节点之前的节点即可也就是这个节点左节点下最右边的节点。如果左子树只有它自己，那他就是那个Y。将Y的值赋给要删除的节点，然后就是第一种情况了将Y原先那个节点删除即可

void remave(TreeNode* &root,int x){
    if(root->val > x) remave(root->left,x);
    else if(root->val < x) remave(root->right,x);
    else{
        if(root->left==NULL && root->right ==NULL){
             root = NULL;
        }
        else if(root->left==NULL){
             root = root->right;
        }
        else if(root->right==NULL){
             root = root->left;
        }else{
             auto p = root->left;
             while(p->right) p = p->right;
             root->val = p->val;
             remave(root->left,p->val);
        }
    }
}

  4.节点的遍历（讲一个其实就可以了）

    1.现有所有数中小于x的最大的数
    2.如果此节点大于x，那就去root的左子树找（递归左子树）
    3.如果此节点小于x，那就去root的右子树找（递归右子树），但是其实这个节点很可能就是答案所以需要再递归出来的值和这个节点中找到最大值max()
    4.为了不让哪些节点为空的影响我们的判断，只要为空我们就返回最小值。

int returnPre(TreeNode* root,int x){
    if(!root) return -INF;
    if(root->val >= x) return returnPre(root->left,x);
    else if(root->val < x) return max(returnPre(root->right,x),root->val);
}

#include <iostream>
#include <algorithm>
using namespace std;
struct TreeNode {
     int val;
    TreeNode *left;
     TreeNode *right;
     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};
TreeNode *root;
#define INF 10001;
void insert(TreeNode* &root,int x){
    //判断是插入右边还是左边
    if(!root) root = new TreeNode(x);
    if(root->val == x) return;
    if(x > root->val)   insert(root->right,x);
    else if(x < root->val)  insert(root->left,x);
}



void remave(TreeNode* &root,int x){
    //先找到那个要删除节点所在处
    //分三种情况
    //1.删除的节点是叶节点，直接删除即可
    //2.删除的节点只有右节点或者左节点 将左节点或者右节点删除即可
    //3.删除的节点有右结点又有左节点，我们只需要知道Y:中序遍历
    //排在这个节点之前的节点即可也就是这个节点左节点下最右边的节点
    //如果左子树只有它自己，那他就是那个Y
    //将Y的值赋给要删除的节点，然后就是第一种情况了将Y原先那个节点删除即可
    if(root->val > x) remave(root->left,x);
    else if(root->val < x) remave(root->right,x);
    else{
        if(root->left==NULL && root->right ==NULL){
             root = NULL;
        }
        else if(root->left==NULL){
             root = root->right;
        }
        else if(root->right==NULL){
             root = root->left;
        }else{
             auto p = root->left;
             while(p->right) p = p->right;
             root->val = p->val;
             remave(root->left,p->val);
        }
    }
}

int returnPre(TreeNode* root,int x){
    //现有所有数中小于x的最大的数
    //如果此节点大于x，那就去root的左子树找（递归左子树）
    //如果此节点小于x，那就去root的右子树找（递归右子树），
    //但是其实这个节点很可能就是答案所以需要再递归出来的值和这个节点中找到最大值max()
    //为了不让哪些节点为空的影响我们的判断，只要为空我们就返回最小值。
    if(!root) return -INF;
    if(root->val >= x) return returnPre(root->left,x);
    else if(root->val < x) return max(returnPre(root->right,x),root->val);
}

int returnEnd(TreeNode* root,int x){
    if(!root) return INF;
    if(root->val <= x) return returnEnd(root->right,x);
    else if(root->val > x) return min(returnEnd(root->left,x),root->val);
}

int main(){
    int n;
    cin>>n;
    while(n--){
        int t,x;
        cin>>t>>x;
        if(t==1){
            insert(root,x);
        }else if(t==2){
            remave(root,x);
        }else if(t==3){
            int a = returnPre(root,x);
            cout<<a<<endl;
        }else if(t==4){
            int b = returnEnd(root,x);
            cout<<b<<endl;
        }
    }
    return  0;
}