国考省考行测:资料分析,两年复合增长率
2022找工作是学历、能力和运气的超强结合体!
公务员特招重点就是专业技能,附带行测和申论,而常规国考省考最重要的还是申论和行测,所以大家认真准备吧,我讲一起屡屡申论和行测的重要知识点
遇到寒冬,大厂不招人,可能很多算法学生都得去找开发,测开
测开的话,你就得学数据库,sql,oracle,尤其sql要学,当然,像很多金融企业、安全机构啥的,他们必须要用oracle数据库
这oracle比sql安全,强大多了,所以你需要学习,最重要的,你要是考网络警察公务员,这玩意你不会就别去报名了,耽误时间!
除了技术,申论和行测也得好好准备
文章目录
- 国考省考行测:资料分析,两年复合增长率
- @[TOC](文章目录)
- 行测:两年的复合增长率
文章目录
- 国考省考行测:资料分析,两年复合增长率
- @[TOC](文章目录)
- 行测:两年的复合增长率
行测:两年的复合增长率

第一年,增长a
第二年,增长b
那整体两年增长多少
a+b+ab
好像就是

懂了吧
记住了就是它
好说
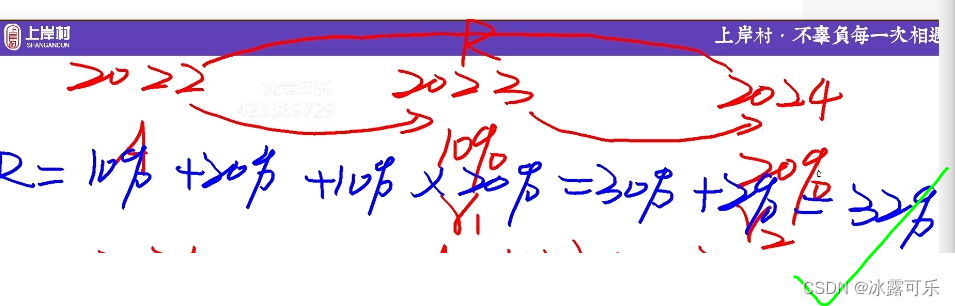
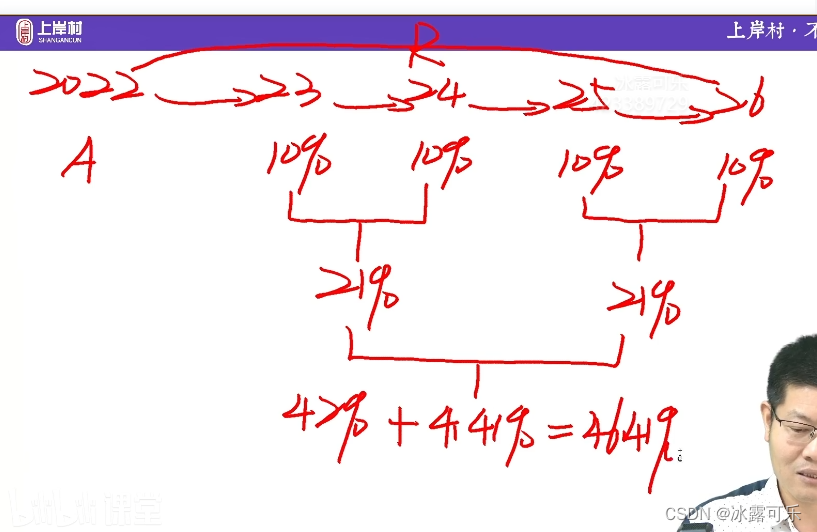
多年复合,完全就是根据2年复合增长率来用二叉树计算
OK
所以2年复合增长率是最根基的
结论1
总增长率高于各年增长率之和
必然的,单独看肯定不行哦
每年增长和,没意义
结论2
每年的增长率相同,可以看做年均增长率,小于总增长率的平均数
年均增长率,小于总增长率的平均
因为结论1懂吧
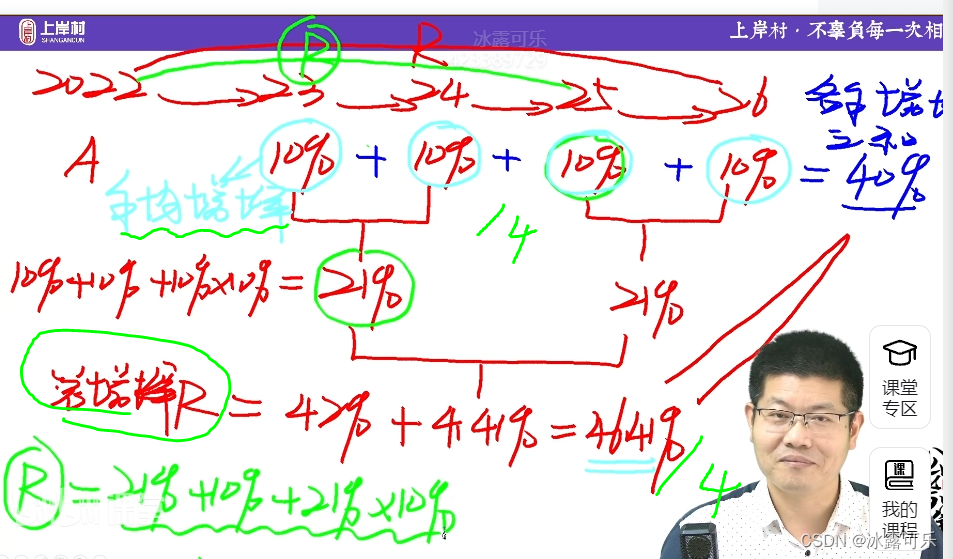
各年增长率不是求和/4,而是各个年份增长率一样,那单独那个就是年均增长率
总复合增长率/4是总增长率平均数

因为年均增长率小于总增长率的平均

所以3年均增长率<3总增长率的平均数
超过48,只有56
OK
记住年均增长率,是各年相同,其中一个就是年均增长率
都是16
22合一,符合增长率

俩方法都行哦

结论1也行哦
没问题

国考题
两年复合增长率
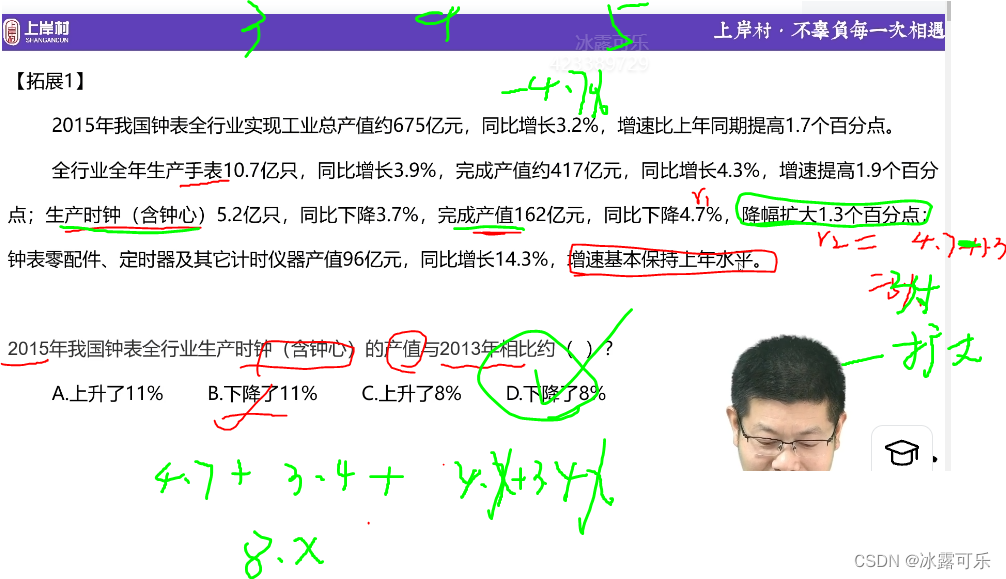
啥叫降幅扩大,是从0—负向
这叫降幅
降幅扩大了,说明原来降得没有这么多,所以才是减
懂了吗
操蛋
扩大就是离远了。
理解错了就C去了操蛋
理解题目的意思很重要。

降幅扩大了,说明距离这0更远了
原来要近一点