算法的基本概念
算法概念
通俗讲:算法是解决问题的一种方法或一个过程
严格讲:算法是解某一特定问题的一组有穷规则的集合
且满足以下性质:
- 有限性:算法在执行有限步之后必须终止
- 确定性:算法的每一个步骤都有精确的定义,要执行的每一个动作都是清晰的,无歧义的
- 输入:一个算法有0个或多个输入,他是由外部提供的,作为算法执行前的初始值或初始状态
- 输出:一个算法有一个或多个输出,这些输出与输入有着特定的关系,实际上是输入的某种函数
- 能行性:指的是算法中有待实现的运算都是基本运算,原则上可以由人们用纸笔在有限时间里精确的完成
算法的时间复杂性分析
有几种方法可以用来分析算法的时间复杂性,如循环次数的统计,基本操作频率的统计,计算步的统计等
- 循环次数的统计:计算多项式O(n),排序(冒泡排序) O(n^2),选手竞技淘汰比赛O(n),洗牌O(nlogn)
- 基本操作频率统计:赋值操作,比较操作,四则运算操作,这些都可以看做基本操作,选取的基本操作执行的频率必须和算法中的任何其他操作一样多
例如冒泡中的比较操作,可以看成基本操作: 归并排序中的赋值操作O(n),收割白菜O(n) - 计算步的统计: 统计算法中所有部分的时间花费 计算步和问题规模n无关,我们可以把一个语句的执行看成一个计算步,或者把连续200个乘法操作看做一个计算步,不能把n次操作看做一个计算步! 可以将
flag = (a+b+c==n)&&(5*a+3*b+c/3==n)&&(c%3==0);看做一个计算步,或者a=b;看做计算步,然后用conut统计次数!
最好情况/最坏情况和平均情况分析
有些算法因为不同输入实例,运行时间可能差别输入规模n的某个阶
- 最好情况: 例如排序算法排升序,输入实例已经是升序,冒泡,插排最好时间复杂性为O(n)
- 最坏情况:例如排升序,输入实例是降序,冒泡,插排最坏时间复杂度为O(n^2)
- 平均情况: 算法运行时间选取算法所有可能输入的平均运行时间
渐进复杂性
算法的输入规模和运行时间的阶
通俗点讲就是保留最大阶,就是我们要求的渐进复杂性
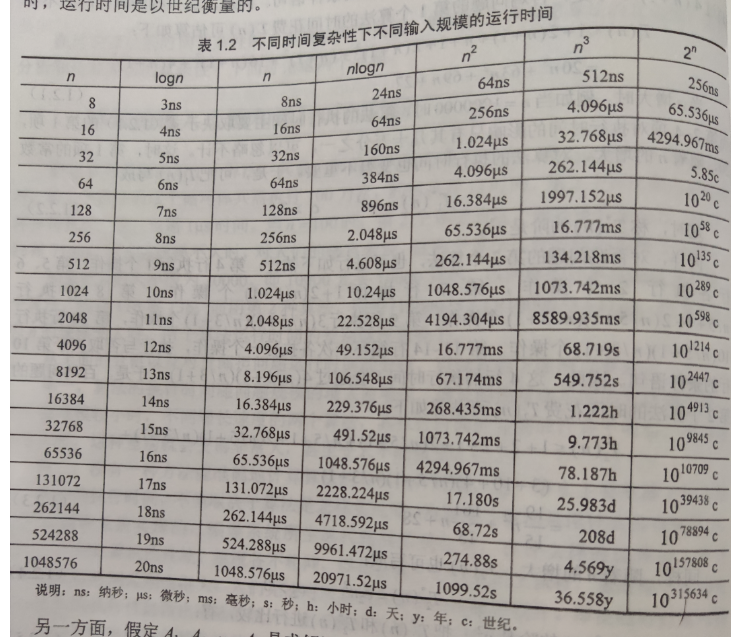
渐进记号
运行时间的上界O记号

运行时间的下界

运行时间的准确界


递归方程解的渐进阶求法


合并排序
- 算法思想:
先将元素划分多组,直到不能划分为止,然后进行区间的合并,合并成有序序列,直到合并成一整个有序序列! - 代码
void merge_sort(int a[],int l,int r,int tmp[])
{
if(l>=r) return;
int mid = l+r>>1;
//递归区间拆分
merge_sort(a,l,mid);
merge_sort(a,mid+1,r);
//进行区间合并
int i = l,j = mid+1,k = 0;
while(i<=mid&&j<=r)
{
if(a[i]<a[j]) tmp[k++] = a[i++];
else tmp[k++] = a[j++];
}
while(i<=mid) tmp[k++] = a[i++];
while(j<=r) tmp[k++] = a[j++];
//拷贝回原数组
for (i = l, j = 0; i <= r; i ++, j ++ ) a[i] = tmp[j];
}
合并过程:
eg: 8 5 3 9 11 6 4 1 10 7 2
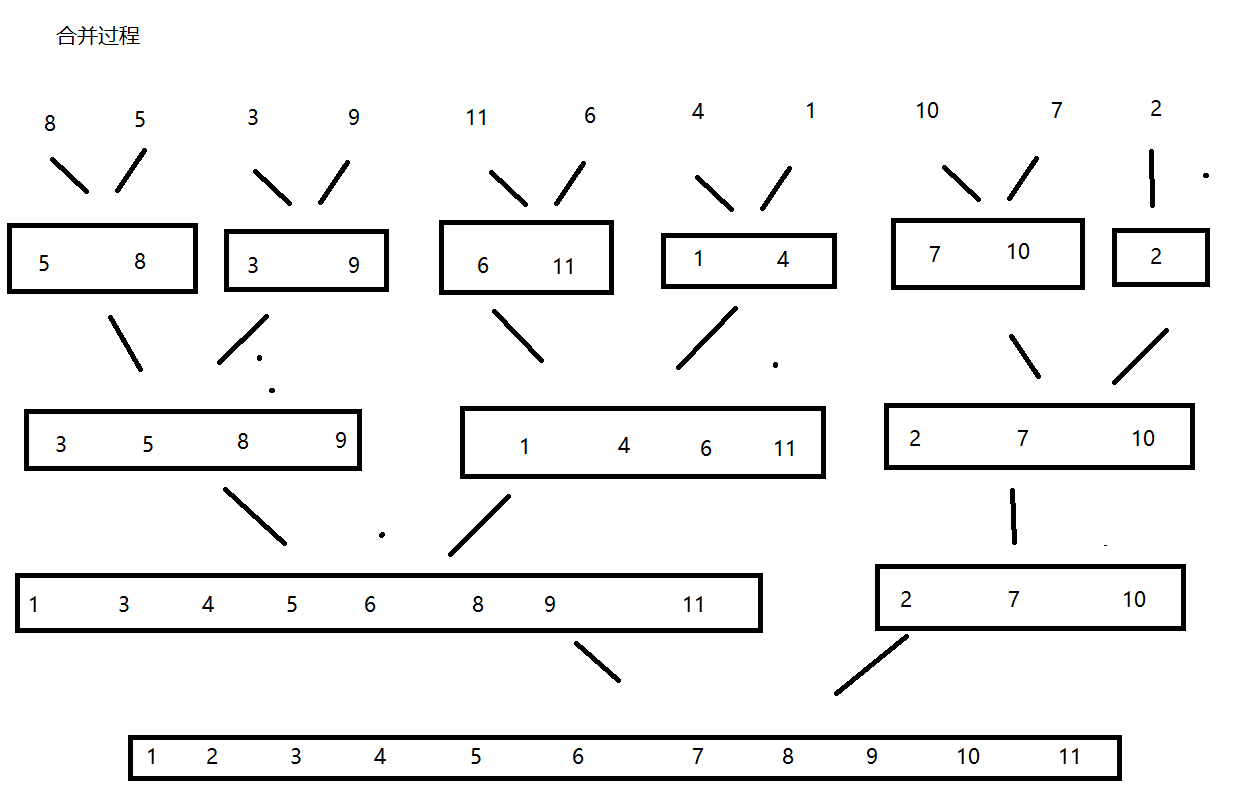
时间复杂度:O(nlogn)
空间复杂度:O(n)
递归和分治法
递归
- 基于归纳的递归算法的思想方法
对于一个规模为n的问题
P(n),归纳法的思想如下:
- 基础步:
a1是问题P(1)的解- 归纳步:对所有的k,
1<k<n,若ak是问题P(k)的解,则p(ak)是问题P(k+1)的解.其中,p(ak)是对ak的某种运算或处理.这里可以将p()看成递归函数!
分治
分治算法思想
在求解一个输入规模为
n,而n的取值有很大的问题时,直接求解往往非常困难.这时,可以先分析问题本身所具有的某些特性,然后从这些特性出发,选择某些适当的设计策略来求解.
例如:把n个输入划分成k个子集,分别对这些子集进行求解,再把所有得到的解组合起来,从而得到整个问题的解,这样,有时可以收到很好的效果.这种方法就是所谓的分治法
eg 最大最小问题:
输入:整数数组
a,数组的起始边界和结束边界l和r
输出:最大运算l,最小元素e_min
void maxmin(int a[],int &e_max,int &e_min,int l,int r)
{
if(r-l<=1) //元素少直接求解
{
if(a[l]<a[r])
{
e_max = max(a[r],e_max);
e_min = min(a[l],e_min);
}
else
{
e_max = max(a[l],e_max);
e_min = min(a[r],e_min);
}
return;
}
int mid,x1,y1,x2,y2;
mid = (l+r)>>1; //划分成2个子区间
maxmin(a,x1,y1,l,mid); //求2个子区间的最大最小值
maxmin(a,x2,y2,mid+1,r);
e_max = max(x1,x2); //合并原数组的最大最小值
e_min = min(y1,y2);
}
求解过程如下图:
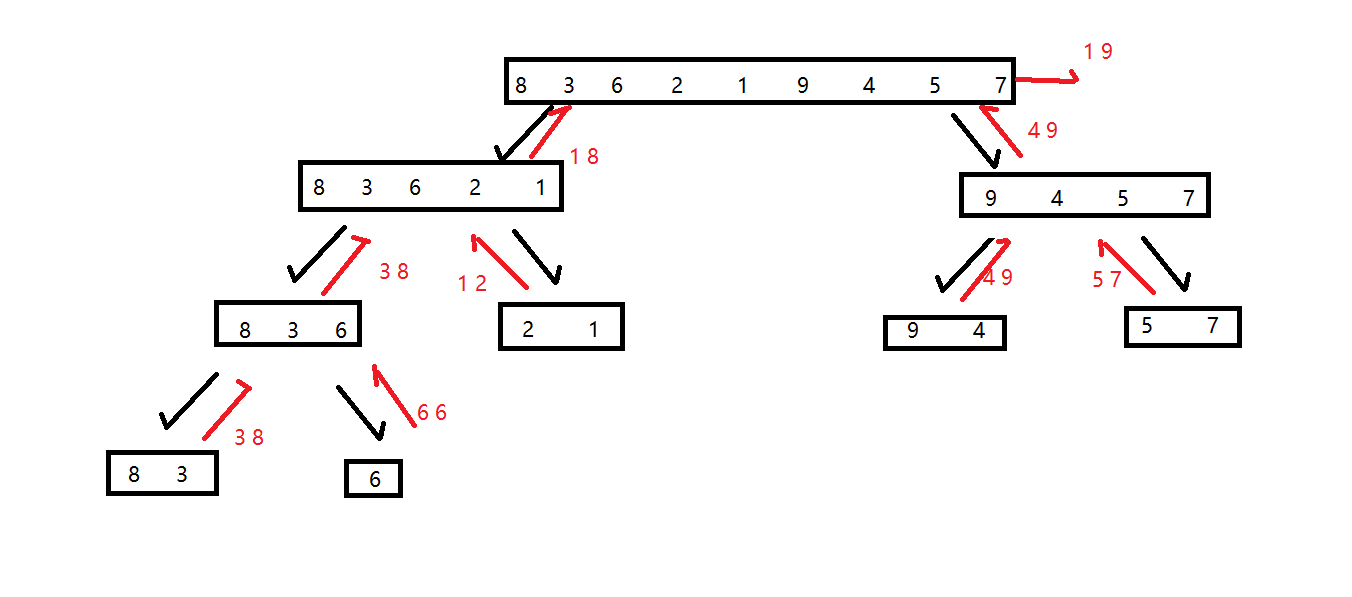
时间复杂度:O(n)
空间复杂度:O(logn) 递归深度
分治法设计步骤
- 划分步:将输入的问题划分成k个子问题
- 治理步:当问题规模大于某个预定义的阀值
n0时,治理步由k个递归调用组成 - 组合步:这一步把各个子问题组合起来
上面3个步骤对应归并排序:
划分步-> 划分子区间
治理步 -> 对区间合并
组合步 -> 拷贝数组
快速排序
算法思想:
把一个序列划分成2个子序列,使得第一个序列的元素都小于第二个序列的所有元素,不断进行划分直到最后构成n个序列,每个序列只有一个元素.这时他们就是有序序列了!
划分步:划分序列
治理步:选择一个基准位置,将区间进行划分,使左边的元素小于基准值,右边元素大于基准值
组合步:这里划分成n个区间后,就已经有序了,也就是整个序列的解
//按枢纽元素划分序列 采用快慢指针
int split(int A[], int low, int high)
{
int k, i = low;
int x = A[low];
//这里的i指向待划分区间的第一个元素,k指向第二个元素!
//这里的k一直往后遍历
for (k = low + 1; k < high; k++)
{
if (A[k] <= x) //这里我们排升序,所以当 A[k]大于x的时候,说明这个位置,符号升序,我们不进入if语句,k指针继续往后
{
//进入了if说明 A[k]比我们选择的基准值x小,应该放在基准值的左边,所以让指针i++,如果k和i不是指向同一个元素就进行交换
i++;
if (i != k)
swap(A[i], A[k]);
}
}
//完成了上述交换后,我们在将基准值和i指向的元素交换,这样也就完成了一次划分
swap(A[low], A[i]);
}
void quick_sort(int A[], int low, int high)
{
int k;
if (low < high) //有区间未划分就会进入if进行划分
{
k = split(A, low, high); //这里返回的k位置,这个元素已经有序,也就是完成了一次划分!
quick_sort(A, low, k - 1);//对 k左边区间进行划分
quick_sort(A, k + 1, high);//对k右边区间进行划分
}
}
算法执行过程
第一次划分:

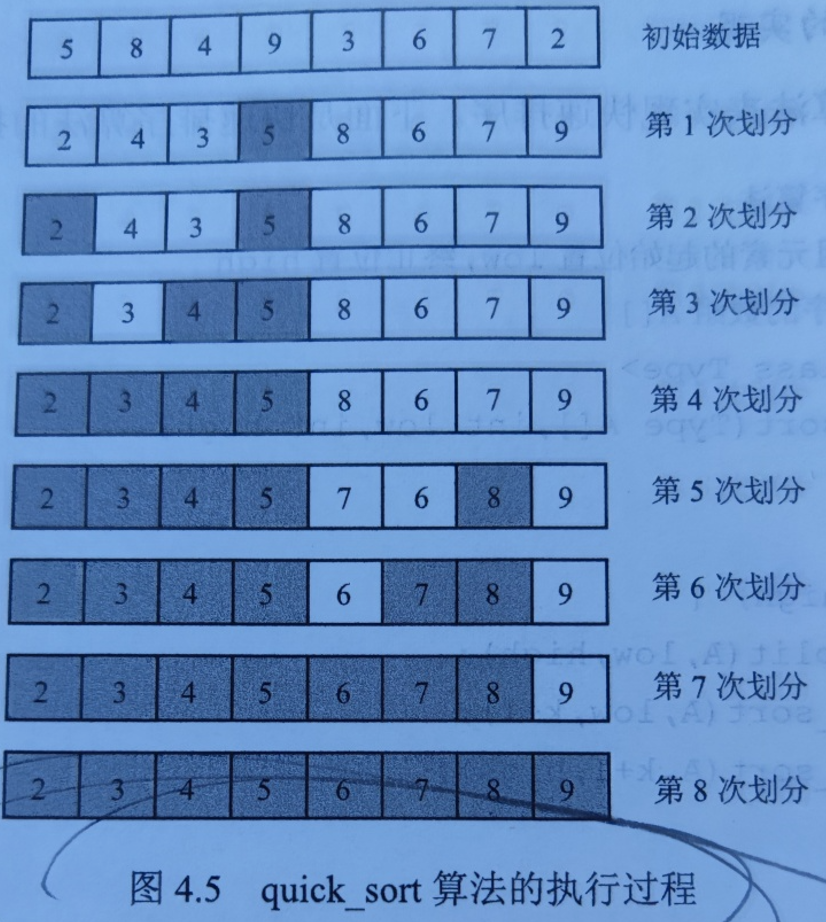
时间复杂度最坏情况: O(n)每次划分都划分成空区间和另一个区间,解决方案基准元素3数取中!
平均复杂度: O(nlogn)
贪婪法
- 设计思想:
贪婪法通常用来解决具有最大值或者最小值优化问题.他犹如登山一样,一步步向前推进,从某一个初始状态出发,根据当前局部的而不是全局的最优决策,以满足约束方程为条件,以使得目标函数的值增加的最快或最慢为准则,选择一个能够最快到达要求的输入元素,以便尽快的构成问题的可行解
适合贪婪法求解的问题满足下面2个重要性质:
- 选择性质
是指所求问题的全局最优解,可以通过一系列局部最优选择来达到.每进行一次选择,就得到一个局部的解,并把所求的问题简化为一个规模更小的类似子问题
- 最优子结构性质
是指一个问题的最优解中包含子问题的最优解
背包问题
这里的背包问题物体可分解,就不介绍了,就是将性价比最高的物品放入到背包中,直到背包放不下此时性价比最高的物品,那就将物品进行分解,然后计算总价值!
单源最短路径问题
Dijkstra狄斯喹诺算法解最短路径
视频链接这是求最短路径的一种算法
算法思想:
多个节点多个连接的边组成的图,我们需要求一个节点到另一个节点的最短路径
我们可以先从第一个节点出发求临近最短的路径的节点,然后确定路径后,再到最短路径节点处重复之前操作,如果当前节点的路径值比之前路径值小就更新路径值,否则不变,直到到达目标节点
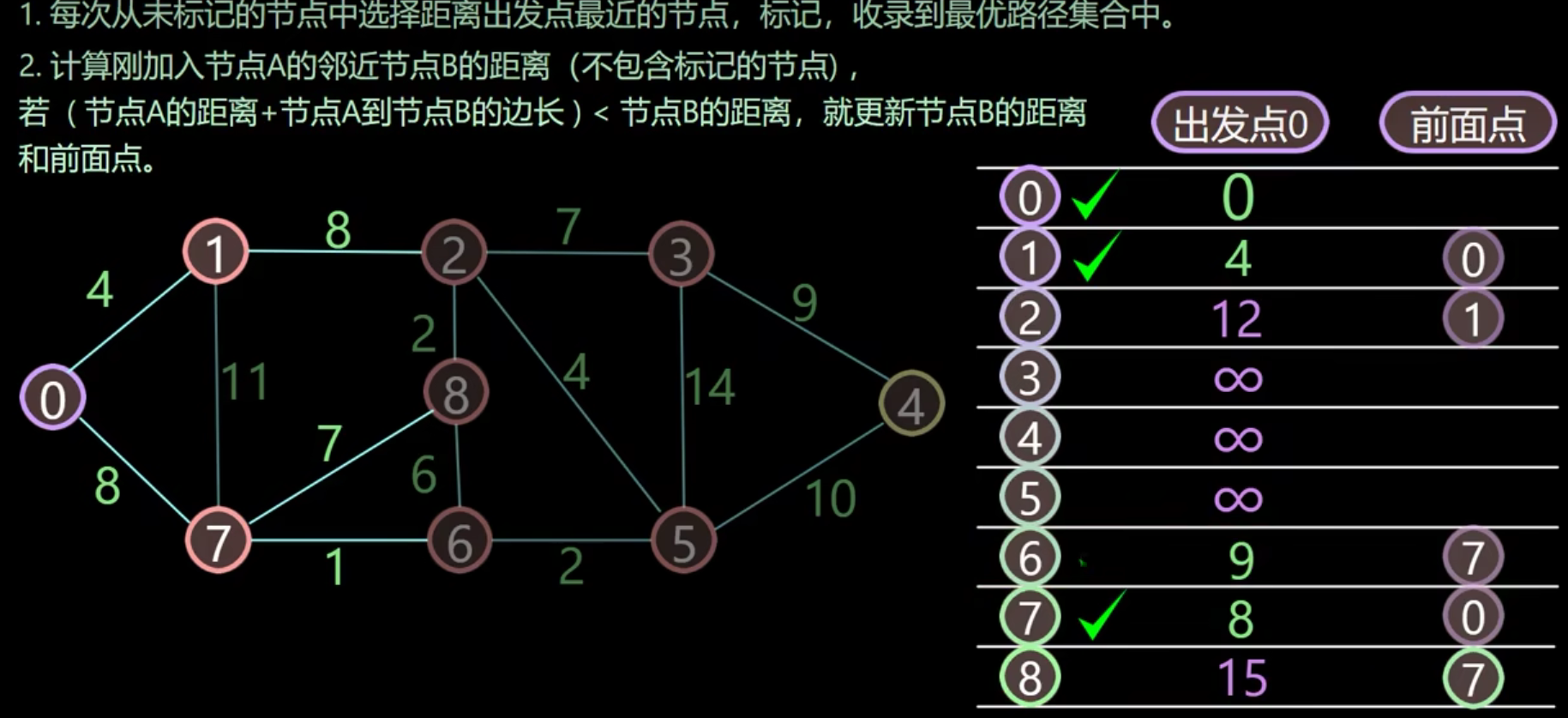
书上例题:
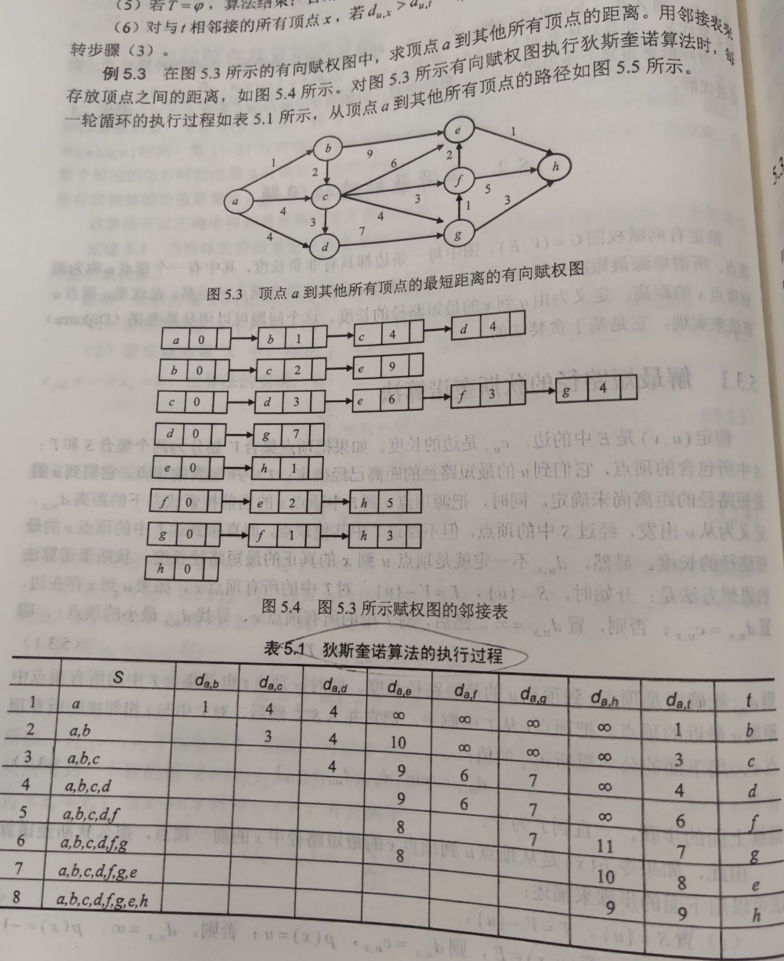
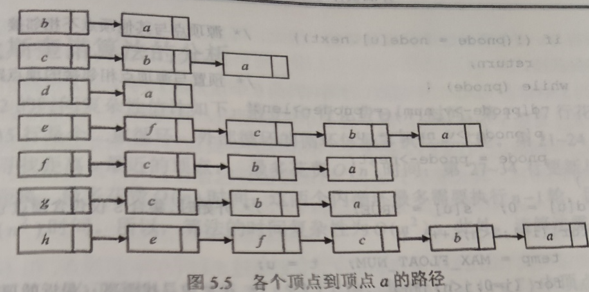
时间复杂度O(n^2) 空间复杂度: O(n)
最小花费生成树问题
最小花费生成树问题应用场景: 例如用图的顶点代表城市,顶点与顶点之间的边代表城市之间的道路或通信线路,用边的权代表道路的长度或通信路线的费用,最小花费生成树问题,就表示城市之间最短的道路或费用最少的通信线路问题.
最小生成树概念:
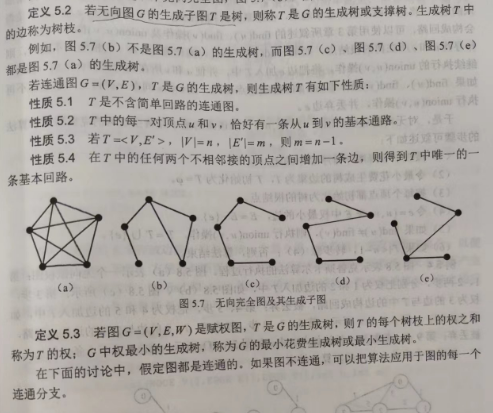
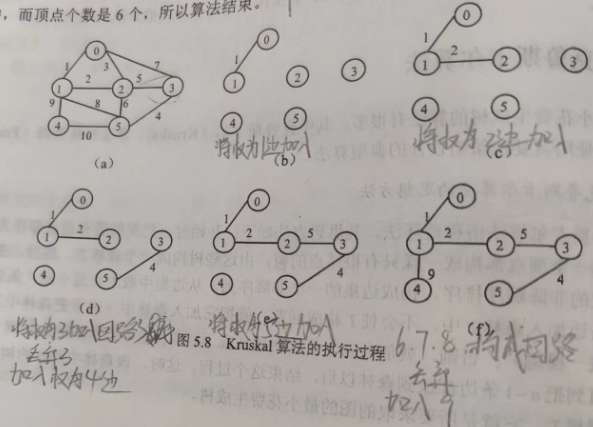
Kruskal克鲁斯卡尔算法
算法思想俗称避环法
开始时将图的所有节点都作为孤立顶点,每个顶点都构成了一颗只有根节点的书,构成了森林T.
然后将所有边按照权值排升序,每次从边集中选择最小权值边,然后加入到到T中,并且不会使当前T构成回路,就加入,否则就丢弃该边,重复上述操作,直到把n-1条边加入后就生成了最小花费生成树
时间复杂度: 完全图O(n^2logn)平面图O(nlogn)空间复杂度:O(n)
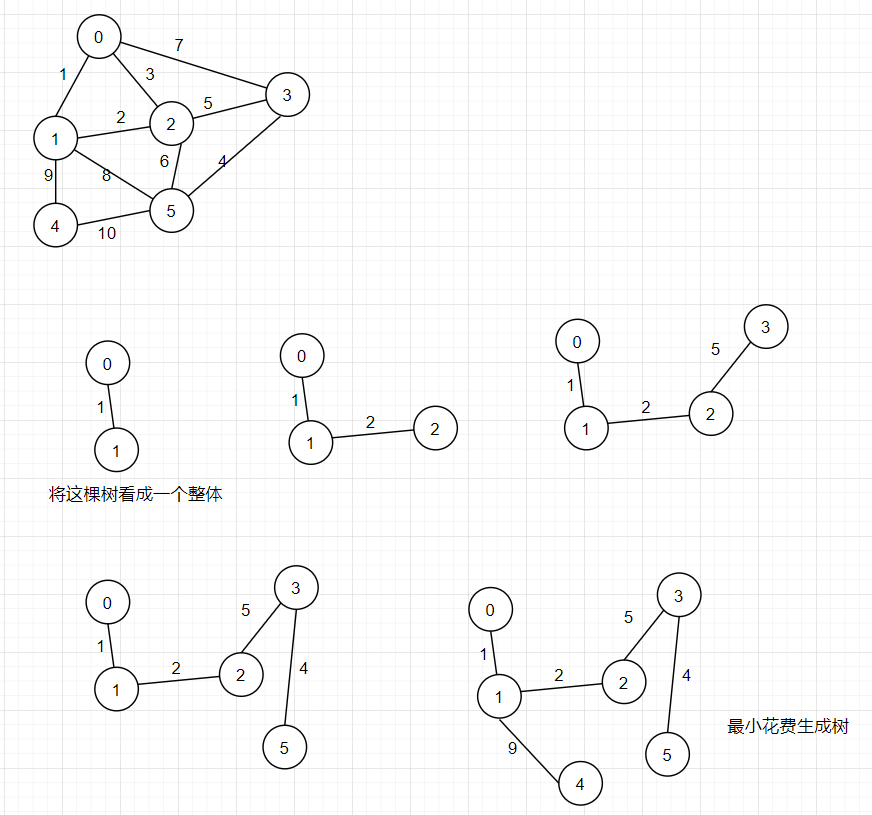
Prim普利姆算法
算法思想:
该算法有点类似狄斯喹诺算法
先从起点位置开始,然后加入与起点相连的最短权值的点,然后将当前树看成一个整体,再加入与当前树相连权值最小的顶点,依次进行直到所有顶点都加入
适用于顶点少,边数多的情况
时间复杂度:O(n^2) 空间复杂度:O(n)
霍夫曼编码问题

通俗点讲哈夫曼树就是一个带权的二叉树,相同的叶节点可以构造出不同哈夫曼二叉树
前缀码和最优二叉树
最优二叉树,就是刚刚哈夫曼树构造WPL为最小
也就是权值越大的越靠近根节点,权值越小的越远离根节点
前缀码就是将哈夫曼树二叉树的每条边编码,左边为0,右边为1进行
到叶子节点,有唯一的前缀码,并且前缀码唯一,任意节点的前缀码不会是另一叶子节点的前缀码

解题步骤
- 构造最优二叉树
- 编码
- 得出每个叶节点的前缀码
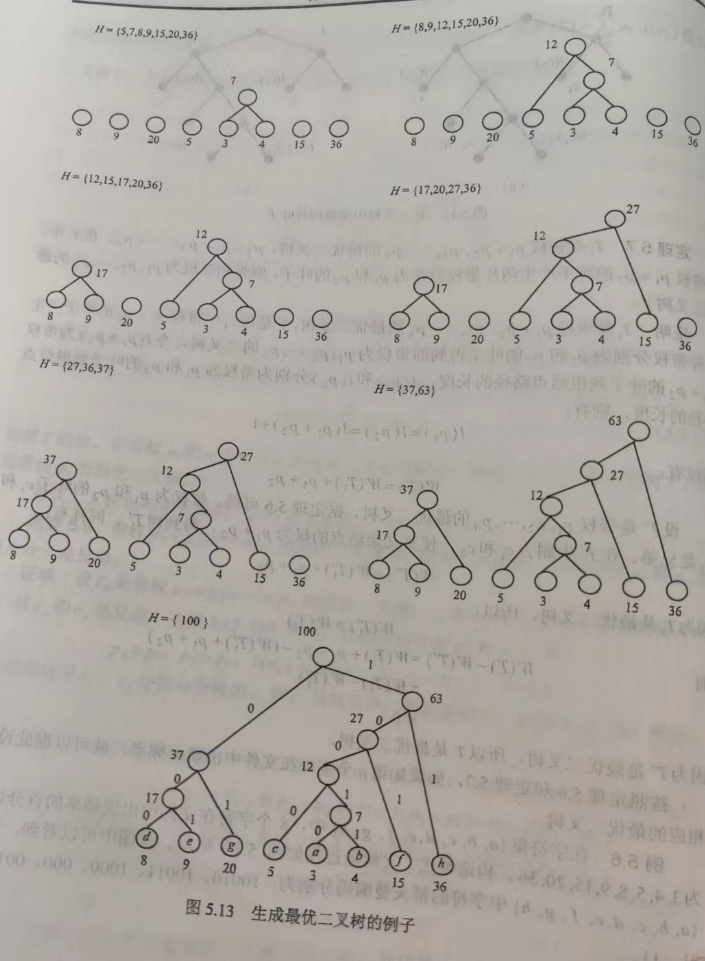
哈夫曼算法时间复杂度:O(nlogn)
动态规划
动态规划思想方法
动态规划的最优决策原理:
对于具有
n个输入的最优解问题,它们的活动过程往往划分为若干个阶段,每一个阶段的决策依赖于前一个阶段的状态,由决策所采取的动作使状态发送转移,成为下一阶段的决策依据.
多段树的最短路径问题
多段树的决策过程
多段树的最短路径问题,是求源点s到达收点t的最小花费通路
决策的第一阶段,确定图中第k-1段的所有顶点到达收点t的花费最小通路
决策的第二阶段,确定图中第k-2段所有节点到达收点t的花费的最小通路
…
详细过程如图所示


0/1背包问题
0/1背包问题中,物体或者被装入背包,或者不装入背包,只有这2种选择,不能分割物体!
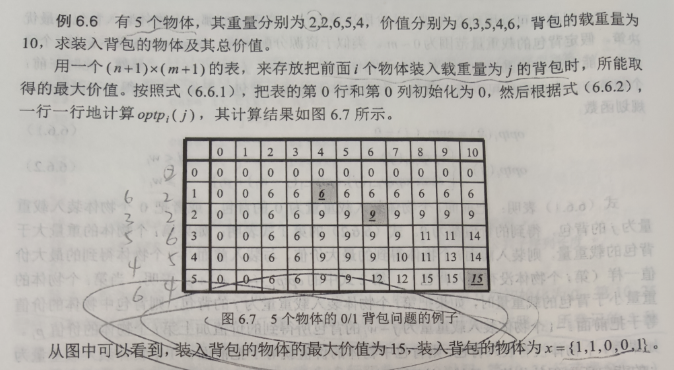
代码实现:
#include<bits/stdc++.h>
using namespace std;
const int MAXN = 1005;
int v[MAXN]; // 体积
int w[MAXN]; // 价值
int f[MAXN][MAXN]; // f[i][j], j体积下前i个物品的最大价值
int main()
{
int n, m;
cin >> n >> m;
for(int i = 1; i <= n; i++)
cin >> v[i] >> w[i];
for(int i = 1; i <= n; i++)
{
for(int j = 1; j <= m; j++)
{
// 当前背包容量装不进第i个物品,则价值等于前i-1个物品
if(j < v[i])
f[i][j] = f[i - 1][j];
// 能装,需进行决策是否选择第i个物品
else
f[i][j] = max(f[i - 1][j], f[i - 1][j - v[i]] + w[i]);
}
}
cout << f[n][m] << endl;
return 0;
}
验证结果
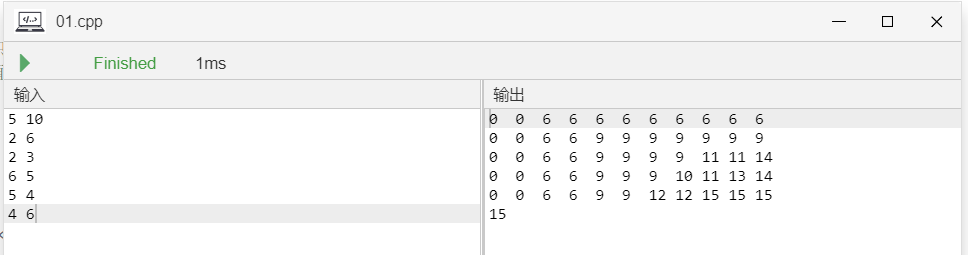




![[Linux打怪升级之路]-秒懂进程地址空间](https://img-blog.csdnimg.cn/ac9fcdad7cff45ae857573fa26e180f4.png)

![[操作系统笔记]基本分段存储管理](https://img-blog.csdnimg.cn/7a92a4177f8145b0b7c3772d121742b5.png)