来源:投稿 作者:小灰灰
编辑:学姐
整体代码请参考深度之眼的《机器学习算法应用实战》
视频链接:https://ai.deepshare.net/p/t_pc/goods_pc_detail/goods_detail/p_5e12aa8734510_IpNUGv5w
1.无监督学习方法---主成分分析
主成分分析(PCA)是一种统计方法,通过正交变换将一组可能存在相关性的变量转换为一组线性不相关的变量,转换后的这组变量叫主成分。应用于降维,高维数据集的探索与可视化,数据压缩,数据预处理。
2.基于协方差矩阵的特征值分解算法
(1)均值归一化
首先加载我们的数据,对数据进行归一化。
加载数据
import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
def loaddata():
data = np.loadtxt('data/pca_data.csv',delimiter=',')
return data
X = loaddata()
plt.scatter(X[:,0],X[:,1])
plt.show()
归一化
def featureNormalize(X):
mu = np.mean(X,axis=0).reshape(1,-1)
sigma = np.std(X,axis=0,ddof=1).reshape(1,-1)
X = (X-mu)/sigma
return X,mu,sigma
(2)计算协方差矩阵
def pca(X,K):
m = len(X)
sigma = np.dot(np.transpose(X),X)/(m-1)
#返回的特征向量要是排序后的
eigenvalues,eigenvectors = np.linalg.eig(sigma)
index = np.argsort(-eigenvalues) # 依照featValue进行从大到小排序
eigenvectors = eigenvectors[:,index]
u_reduce = eigenvectors[:, 0:K]
return np.dot(X, u_reduce),eigenvectors
(3)计算协方差矩阵的特征向量
X,mu,sigma = featureNormalize(X)
Z,eigenvectors = pca(X,1)
print(Z)
最终显示出结果:
def recoverData(Z, U, K):
U_reduce = U[:,0:K]
X_rec = np.dot(Z,np.transpose(U_reduce))
return X_rec
def plotData(X_orgin,X_rec):
plt.scatter(X_orgin[:,0],X_orgin[:,1])
plt.scatter(X_rec[:, 0], X_rec[:, 1],c='green')
plt.show()
X_rec = recoverData(Z,eigenvectors,1)
plotData(X,X_rec)
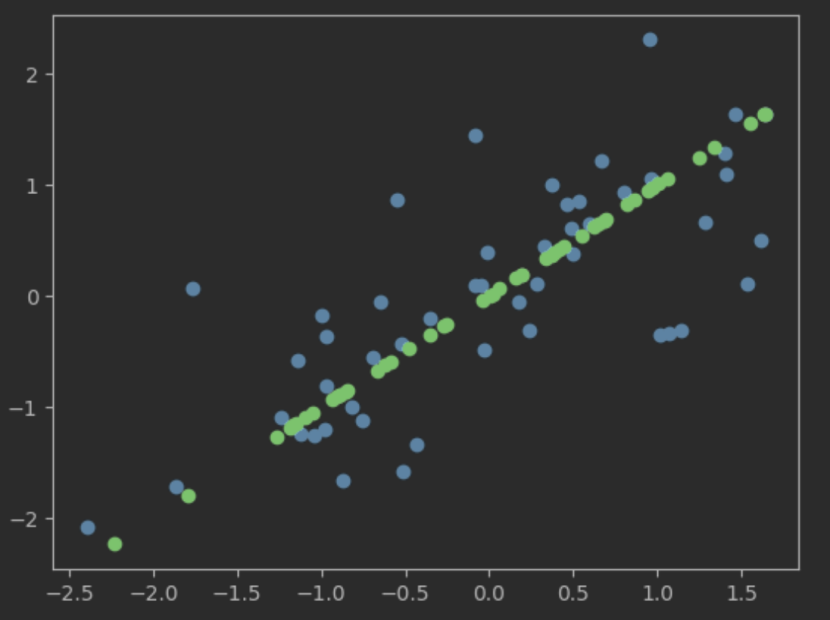
根据图,我们可以观察到二维数据降维到一维坐标点(绿色点)。
3.基于数据矩阵的奇异值分解
(1)均值归一化
我们使用刚才的数据集,进行归一化
def featureNormalize(X):
mu = np.mean(X,axis=0).reshape(1,-1)
sigma = np.std(X,axis=0,ddof=1).reshape(1,-1)
X = (X-mu)/sigma
return X,mu,sigma
(2)对数据矩阵进行分解
def pca(X,K):
u,s,vT = np.linalg.svd(X,full_matrices=0)
return X.dot(vT.T[:, 0:K]),u,s,vT
(3)显示降为后的数据
X,mu,sigma = featureNormalize(X)
Z,u,s,vT = pca(X,1)
print(Z)
def recoverData(Z, vT, K):
V_reduce = vT[:,0:K]
X_rec = np.dot(Z,np.transpose(V_reduce))
return X_rec
def plotData(X_orgin,X_rec):
plt.scatter(X_orgin[:,0],X_orgin[:,1])
plt.scatter(X_rec[:, 0], X_rec[:, 1],c='red')
plt.show()
X_rec = recoverData(Z,vT,1)
plotData(X,X_rec)
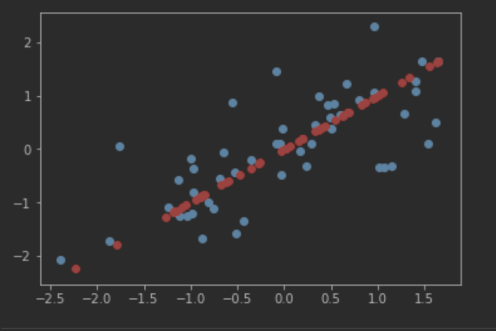
红色点是蓝色点降维后的可视化。
4.图像进行压缩
可以任意找一张图片进行PCA的压缩。
首先读取一张图片
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.image as mpimg
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
img=mpimg.imread('data/jjq.jpg')
如果想显示看一下图片,可以
plt.imshow(img)
plt.show()
查看数据的维度
img.shape
我们把三维的照片变成二维的
X = img.reshape(1200,1200)
进行数据标准化
X = StandardScaler().fit_transform(X)
使用PCA进行降维
model = PCA(n_components=50)
Z = model.fit_transform(X)
print("贡献比=",np.sum(model.explained_variance_ratio_))
接下来,我们要把图片进行还原
X_rec = model.inverse_transform(Z)
X_rec = X_rec.reshape(800,600,3)
进行还原后的显示
plt.imshow(X_rec)
plt.show()
大家可以看看自己上传的图片显示出的结果
关注下方【学姐带你玩AI】🚀🚀🚀
回复“机器学习”领取必读书籍PDF+免费课件
码字不易,欢迎大家点赞评论收藏!