1.分发饼干

455. 分发饼干

贪心的思路就是：小的饼干尽量去匹配胃口小的孩子，这样才能实现尽可能多孩子吃到。

那么代码就很好写了：

1.排序g和s，这样方便查找小的数

2.饼干的位置不停遍历，对应我们需要一个ret代表当前孩子位置

3.如果当前位置为孩子的数量，说明ret记录下所有的孩子，直接返回即可。如果当前孩子的胃口刚好小于等于饼干遍历的位置，说明此时这个孩子是满足要求的，那么ret++，此外，说明条件不满足，我们需要找下一个饼干去判断是否满足大于或者等于小孩胃口的条件

class Solution {
public:
    int findContentChildren(vector<int>& g, vector<int>& s) {
        sort(g.begin(),g.end());
        sort(s.begin(),s.end());
        int ret = 0;
        for(int i=0;i<s.size();i++)
        {
            if(ret==g.size())
                break;
            if(g[ret]<=s[i])
                ret++;
        }
        return ret;
    }
};

2.摆动序列

376. 摆动序列

贪心的思路：如果前一个的趋势和后一个的趋势一样，那么我们就刨除掉当前的点。这样就能有最长的序列了

1.先介绍变量用来记录什么：

int ret = 1：代表返回的摆动点数，由于默认一个点就是一个数，那么我们初始化就变为1

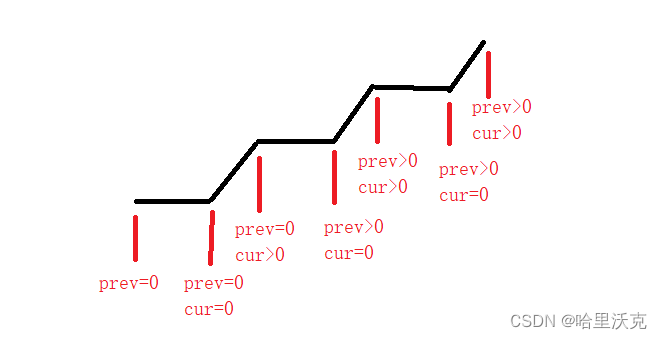
int prev = 0 ：代表前一次波动的趋势，不过要注意的是，我们开始设置为平波动是因为第一个位置不需要比较，默认计数一次；后面prev不会用来记录平波动，这是我用来判断连续平波和上坡交替出现时的特殊点，之所以这样设计，是让prev代表从ret没有变化后整体的趋势，如果cur=0，此时不能代表前面的就一定是有起伏的，那么也就不能让ret++。

int cur = 0：当前位置与前一个位置的趋势情况。

prev和cur的比较就是用来判断ret是否加一的条件！！

2.由于第一个数（下标为0），已经被我们记录下来了，那么循环的开始就从下标1开始。先更新cur为当前的数减去前一个数。随后判断此时的prev和cur条件

*由于开始我们设置的prev=0，所以此时的条件一定有一个是(prev==0&&cur!=0)，因为我们有一个条件是不能忽略的：最开始就有一个上升趋势，那么当前的位置是需要加一的操作才能记录下，所以ret++

*(prev>0&&cur<0)||(prev<0&&cur>0)，那么就是一个起伏，说明当前的趋势和上一次趋势是相反的，那么是可以将当前的ret++

*上面两个判断都需要更新节点前一个的趋势prev=cur；那么值得注意的是，当cur=0时，我们不更新prev，就是条件1介绍：prev是必须要用来表示ret不变时，整体的趋势，这样才能判断下一次的趋势和整体趋势区别，才能对ret进行操作

class Solution {
public:
    int wiggleMaxLength(vector<int>& nums) {
        int ret = 1;
        int prev = 0;
        int cur = 0;
        if(nums.size()==1)
            return ret;
        for(int i=1;i<nums.size();i++)
        {
            cur = nums[i]-nums[i-1];
            if((prev>0&&cur<0)||(prev<0&&cur>0)||(prev==0&&cur!=0))
            {
                ret++;
                prev=cur;
            }
        }
        return ret;
    }
};

3.最大子数组和

53. 最大子数组和

贪心的思路：如果累加的总数小于0，那么后面的正数会影响，也就是说下一个位置的整数并没有起到使得总和变大的作用，那不如从下一个位置重新开始。

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        int ret = nums[0];
        int tmp = 0;
        for(int i=0;i<nums.size();i++)
        {
            tmp+=nums[i];
            if(ret<tmp)
                ret=tmp;
            if(tmp<0)
                tmp=0;
        }
        return ret;
    }
};