1 知识框架

2 栈

定义：只允许在一端进行插入或删除得到线性表
栈的数学性质：n个不同元素进栈，出栈的不同排列有

2.1 顺序栈

定义：

typedef struct
{
	int data[MaxSize];
	int top;   // 栈顶指针  初始化top = -1，栈顶元素：S.data[top]
}Stack;

1.进栈

bool Push(Stack &s,int x)    //为什么用&，这里不用&，传的就是形参，存进来的数据不会改变内存中的栈
{
	if(s.top == MaxSize - 1)
		return false;
	s.data[++ s.top] = x;
	return true;
}

2.出栈

bool Pop(Stack &s,int &x)
{
	if(s.top == -1)
		return false;
	x = s.data[top --];
	return true;
}

2.2 链式栈

定义：

typedef struct Linknode
{
	int data;
	struct Linknode *next;
}*Stack;

3 队列

定义：在表的一端进行插入，在表的另一端进行删除的线性表。

3.1 顺序队列

定义：

typedef struct
{
	int data[MaxSize];
	int front,rear;   //初始化 front = rear = 0;
}Queue;

1.进队

bool Push(Queue &s,int x)
{
	if(s.rear == MaxSize)    //并不是真正的队满，假溢出
		return false;
	s.data[rear ++] = x;
	return true;
}

2.出队

bool Pop(Queue &s,int &x)
{
	if(s.front == s.rear)
		return false;
	x = s.data[front ++];
}

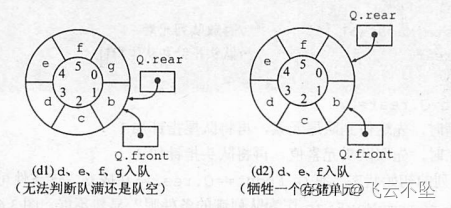
3.2 循环队列

1.初始：Q.front = Q.rear = 0;
2.入队：Q.rear = (Q.rear + 1) % MaxSize;
3.出队：Q.front = (Q.front + 1) % MaxSize;
4.队长:（Q.rear - Q.front + MaxSize） % Maxsize;
5.判空：Q.rear == Q.front;
6.判满：Q.front == (Q.rear + 1) % MaxSize //队列留出一个位置作为队列判满的条件，不然rear == front可以是队空，也可以是队满。

3.3 链式队列

定义：

typedef struct LinkNode
{
	int data;
	struct LinkNode *next;
}LinkNode;                //队列节点

typedef struct 
{
	LinkNode *front,*rear;
}*LinkQueue;    //无名结构体    使用：  别名 变量名   LinkQueue linkQueue;

4 数组

4.1 二维数组

二维数组在内存中的位置的两种映射方式。
1.先行后列

//位置计算方法  L是每个数组元素所占的存储空间大小  int  4个字节
A[2][3]
ADD(A[i][j]) = ADD(A[0][0])+(i * 4 + j) * L;

2.先列后行

//位置计算方法  L是每个数组元素所占的存储空间大小  int  4个字节
A[2][3]
ADD(A[i][j]) = ADD(A[0][0])+(j * 3 + i) * L;

4.2 特殊数组的压缩存储