Knuth-Morris-Pratt 算法（简称 KMP）是由高德纳（Donald Ervin Knuth）和沃恩·普拉特在1974年构思，同年詹姆斯·H·莫里斯也独立地设计出该算法，最终三人于1977年联合发表。该算法较Brute-Force算法有较大改进，主要是消除了目标串指针的回溯，从而使算法效率有了某种程度的提高。

01、KMP算法（Java描述）

如何消除了目标串指针的回溯呢？先看一个示例，假设目标串s="aaaaab"，模式串t="aaab"，看其匹配过程：

（1）当进行第一趟匹配时，失配处为i=3/j=3。尽管本趟匹配失败了，但得到这样的启发信息，s的前3个字符"s0s1s2"与t的前3个字符"t0t1t2"相同，显然"s1s2"="t1t2"是成立的。

（2）从t中观察到"t0t1"="t1t2"，这样就有"s1s2"="t1t2"="t0t1"。按照BF算法下一趟匹配应该从s1/t0比较开始，而此时已有"s1s2"="t0t1"，没有必要再做重复比较，下一步只需将s3与t2开始比较即做s3/t2的比较，如图1所示。

这种“观察信息”就是失配处为si/tj时，需要找出tj前面有多少个字符与t开头的字符相同。采用一个next数组表示，即next[j]=k表示有"t0t1…tk-1"="tj-ktj-k+1…tj-1"成立，那么如何求next[j]呢？

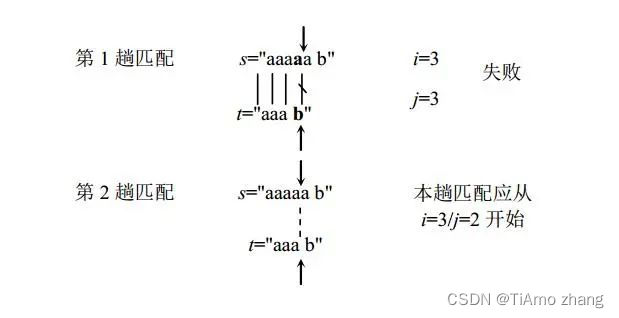
■ 图1 利用启发信息进行的匹配

考虑失配处模式串t中字符tj前面的子串"t0t1…tj-1"，定义其前缀（真前缀更加准确些）为除了自身以外全部头部组合，即以首字符t0开头的除了自身以外的子串。定义其后缀（真后缀更加准确些）为除了自身以外全部尾部组合，即以尾字符tj-1结尾的除了自身以外的子串。定义其中最长的相同前、后缀为M串，则next[j]就是该M串的长度。next[j]=k的含义如图4.9所示，其中前缀和后缀可以重叠。

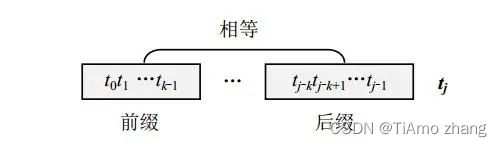
■ 图2 next[j]=k的含义

例如，t="abcdabd"，求next[6]的过程是，t6='d'，t中它前面的串是"abcdab"（恰好含6个字符），其前缀有"a"，"ab"，"abc"，"abcd"，"abcda"（注意前缀不包含自身"abcdab"），其后缀有"b"，"ab"，"dab，"cdab"，"bcdab"（注意后缀不包含自身"abcdab"），前、后缀中相同只有"ab"，它就是t6的M串，含2个字符，所以next[6]=2。

在求模式串t中tj的M串时需要注意以下几点：

（1）M串至多从t1开始的，也就是说，j-k≥1，或者k<j。

（2）M串与t中字符位置相关，除了t0外，每个位置都有一个M串（M串可以为空，此时k=0）。

（3）如果tj有多个相同的前、后缀，应该取最大长度的相同前、后缀作为M串。

（4）next[j]=k中k表示M串中的字符个数。

归纳起来，求模式t的next[j]（0≤j≤m-1）数组的公式如下：

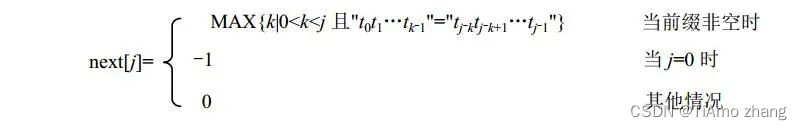
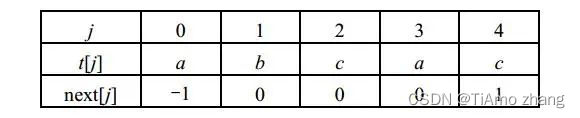
对于模式串t="abcac"，求其next数组的过程如下：

（1）对于序号0，规定next[0]=-1。

（2）对于序号1，置next[1]=0，实际上next[1]总是为0。

（3）对于序号2，t2前面的子串为"ab"（含2个字符），前缀为"a"，后缀为"b"，对应的M串为空，置next[2]=0。

（4）对于序号3，t3前面的子串为"abc"（含3个字符），前缀为"a"和"ab"，后缀为"c"和"bc"，对应的M串为空，置next[3]=0。

（5）对于序号4，t4前面的子串为"abca"（含4个字符），前缀为"a"、"ab"和"abc"，后缀为"a"、"ca"和"bca"，相同的前、后缀只有"a"，对应的M串为"a"，它只有一个字符，置next[4]=1。

这样模式串t对应的next数组如表1所示。

表1 模式串的next数组值

求模式串t的next数组的算法如下：

public static void GetNext（String t,int nest[]）
{
int j = 0,k = -1;
Next[0] = -1;
while(j < t.length() - 1)
{
if(k == 1 ||t.length() - 1)
{
j++;k++;
next[j] = k;
}
else k = next[k];
}

}

上述算法的思路是先置next[0]=-1（为了区分j的不同取值，取值-1表示j=0 的特殊情况），再由next[j]求next[j+1]（1≤j≤m-1），初始k置为-1（表示从j=0开始求其他next元素值）。

假设next[j]=k，即有"t0t1…tk-1"="tj-ktj-k+1…tj-1"成立：

（1）若tj=tk，可以推出"t0t1…tk-1tk"="tj-ktj-k+1…tj-1tj"（共k+1个字符）成立，说明字符tj+1的M串的长度为k+1，所以置j++，k++，next[j]=k，如图3所示。

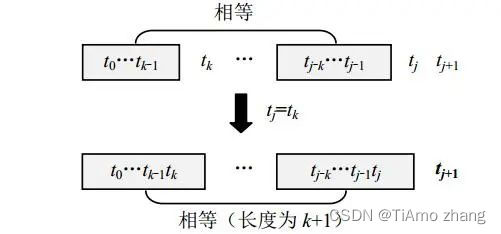
■ 图3 tj=tk的情况

（2）若tj≠tk，则说明tj+1之前不存在长度为next[j]+1（或者k+1）的和t0起匹配的子串。那么是不是必须从k=0开始试探来求next[j+1]呢？

可以这样来提高效率，如果next[k]=k'（k'<k），说明字符tk有一个长度为k'的M前缀，若tj=tk'，那么就有next[j+1]=next[k']+1，推导过程如图4.11所示。当然，若tj≠tk'，需要置k'=next[k']继续做下去，最多到k'=-1为止，这时的结果是next[j+1]=k'+1=0。

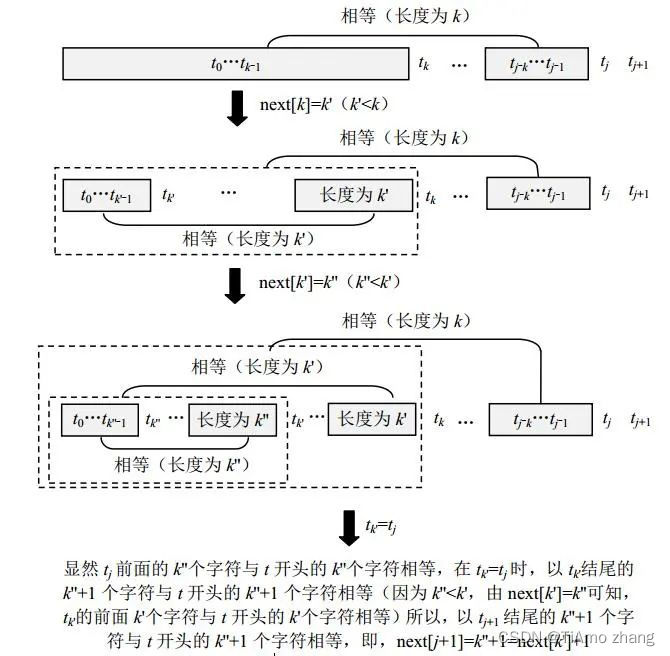
■ 图4 tj≠tk的情况

由这两种情况分析可知，GetNext()算法的时间复杂度为O(m)，m为t的长度。

例如，t="aaaabaaaaabc"，按照GetNext算法求出nextt[0..8]如表2所示，现在由next[9]求next[10]。此时next[9]=4，j=9，k=4，由于t[9]≠t[4]，置k=next[k]=3，而t[9]=t[3]成立，所以执行j++，k++，next[10]=next[4]+1=4，如图5所示。从中看出不需要从k=0开始，而是从k=next[k]的位置开始比较效率更高。

表2 模式串的next数组部分值

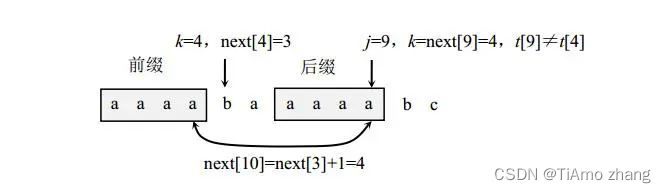
■ 图5 求next[10]

下面讨论KMP算法的一般情形，设目标串s="s0s1…sn-1"，模式串t="t0t1…tm-1"，在进行一趟匹配（该趟以si-j/t0开始比较的）时，出现如图6所示的情况。

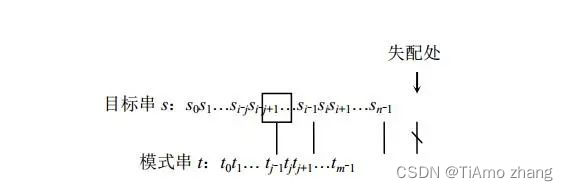
■ 图6 主串和模式串匹配的一般情况

此时失配处为si/tj，显然有"t0t1…tj-1"="si-jsi-j+1…si-1"，假设next[j]=k（k<j），考虑k的各种情况：

（1）若next[j]≠j-1，即有"t0t1…tj-2"≠"t1t2…tj-1"（含j-1个字符，若相等则next[j]=j-1），则回溯到si-j+1开始与t匹配必然“失配”，理由很简单，由这两个式子可知一定有"t0t1…tj-2"≠"si-j+1si-j+2…si-1"（含j-1个字符），既然如此，回溯到si-j+1开始与t匹配可以不做，如图7所示。简单地说，若next[j]≠j-1，则按BF算法做下一趟即si-j+1/t0开始的比较是不必要的（因为这一趟一定失败）。

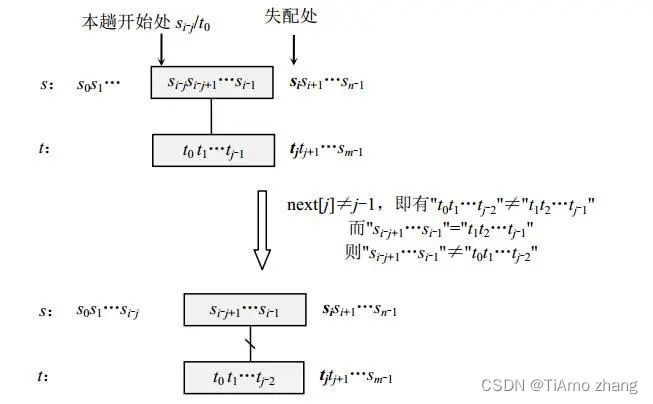
■ 图7 说明回溯到si-j+1是没有必要的

（2）若next[j]≠j-2，即有"t0t1…tj-3"≠"t2t3…tj-1"（含j-2个字符，若相等则next[j]=j-2），则回溯到si-j+2开始与t匹配必然“失配”，因为有"t2…tj-1"="si-j+2…si-1"，很容易推出"t0t1…tj-3"≠"si-j+2…si-1"。简单地说，若next[j]≠j-2，则按BF算法做再下一趟即si-j+2/t0开始的比较的这一趟是不必要的。

（3）以此类推，直到对于某一个值k，有next[j]=k成立，也就是说有"t0t1…tk-1"="tj-ktj-k+1…tj-1"（含k个字符，多于k个字符时不成立），这样有"tj-ktj-k+1…tj-1"="si-ksi-k+1…si-1"="t0t1…tk-1"，说明下一次可直接比较si和tk，这样可以直接把当前趟匹配“失配”时的模式t从当前位置直接右滑j-k位。而这里的k即为next[j]，如图8所示。然后继续做下去。

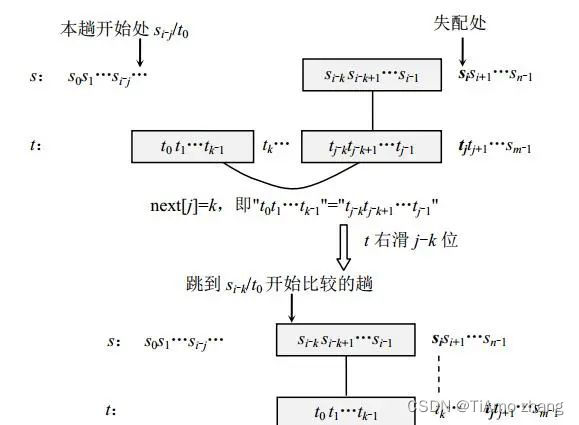
■ 图8 模式串右滑j-k位

从中看出，与BF算法相比，KMP算法不仅仅减少了一趟中字符比较次数，还可能会减少匹配的趟数。如果说BF算法是i=0，1，2，…，连续匹配的，而KMP算法是跳跃的匹配，上述过程也证明这些跳过的趟是不必要的匹配。

综上，KMP算法的过程是，设s为目标串，t为模式串，并设i指针和j分别指示目标串和模式串中正待比较的字符（i和j的均从0开始）。

（1）若有si=tj，则i和j分别增1。

（2）否则，失配处为si/tj，i不变，j退回到j=next[j]的位置（即模式串右滑），再比较si和tj，若相等则i、j各增1，否则j再次退回到下一个j=next[j]的位置，依次类推，直到出现下列两种情况之一：一种情况是j退回到某个j=next[j]位置时有si=tj，则指针各增1后继续匹配；另一种情况是j退回到j=-1时，此时令i、j指针各增1，即下一次比较si+1和t0。

简单地说，KMP算法利用已经部分匹配的有效信息，保持i指针不回溯，通过修改j指针，让模式串尽量地移动到有效的位置。

对应的KMP算法如下：

public static int KMP(String s,String t)
{
int [] next=new intMaxSize];
int i=0,j=0;
GetNext(t,next);
while (i<s.length()&& j<t.length()
{
if(j=--1| s.charAt(i)--t.charAt(i);
{
i++;
j++;
}
else j = next[j];
}
if(j>=t.length()) return(i-t.length();
else return(-1);
}

设目标串s的长度为n，模式串t长度为m，在KMP算法中求next数组的时间复杂度为O(m)，在后面的匹配中因主串s的下标i不减即不回溯，比较次数可记为n，所以KMP算法总的时间复杂度为O(n+m)。

【例1】设主串s="ababcabcacbab"，模式串t="abcac"。给出KMP进行模式匹配的过程。

解：模式串对应的next数组如表4.1所示，其采用KMP算法的模式匹配过程如图4.16所示。首先i=0，j=0，匹配到i=2/j=2失败为止。i值不变（不回溯到前面），修改j=next[j]=0，匹配到i=6/j=1失败为止。i值不变（不回溯到前面），修改j=next[j]=1，匹配到i=10/j=5（t的字符比较完），返回i-t.length=5，表示t是s的子串，且位置为5。

■ 图9 KMP算法的模式匹配过程

上述next数组在某些情况下尚有缺陷。例如，设主串s="aaabaaaab"，模式串t="aaaab"。t对应的next数组如表3所示

表3模式串t的next数组值

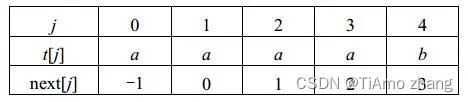
两串匹配的过程如图10所示，从中看到，当i=3/j=3时，s3≠t3，由next[j]的指示还需进行i=3/j=2，i=3/j=1，i=3/j=0等3次比较。实际上，因为模式中的第1、2、3个字符和第4个字符都相等，因此，不需要再和主串中第4个字符相比较，而可以将模式一次向右滑动4个字符的位置直接进行i=4/j=0时的字符比较。

■ 图10 KMP算法的模式匹配过程

上述示例中存在的问题可以通过改进next数组得到解决，将next数组改为nextval数组，与next[0]一样，先置nextval[0]=-1。假设求出next[j]=k，现在失配处为si/tj，即si≠tj，

（1）如果有tj=tk成立，可以直接推出si≠tk成立，没有必要再做si/tk的比较，直接置nextval[j]=nextval[k]]（nextval[next[j]]），即下一步做si/tnextval[j]的比较。

（2）如果有tj≠tk，没有改进的，置nextval[j]=next[j]。

改进后的求nextval数组的算法如下：

public static void GetNextval(String t,int []nextval)
{
intj=0,k=-1;
nextval[0]=-l;
while (j<t.length()-I)
{
if(k==-1||t.charAt(j)==t.charAt(k))
{
j++;k++;
if(t.charAt(j)!=t.charAt(k))nextval[j]=k;
else
nextvallj]=nextval[k];
}
}
}

改进后的KMP算法如下:

public static int KMP1(String s,String t)
{
int [] nextval=new intMaxSize];
int i=0,j=0;
GetNextval(t,nextval);
while (i<s.length() && j<t,length())
{
if(j==-l] s.charAt(i)==t.charAt(j))
{
i++;
j++;
}
else j = nextval[j];
}
if(j >= t.length())
return(i-t,length());
else return(-1);
}

与改进前的KMP算法一样，本算法的时间复杂度也为O(n+m)。

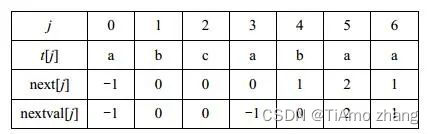
【例2】设目标串为s="abcaabbabcabaacbacba"，模式串t="abcabaa"。计算模式串t的nextval函数值。并画出利用KMP算法进行模式匹配时每一趟的匹配过程。

解：模式串t的nextval函数值如表4所示。

表4 模式串t的nextval函数值

利用KMP算法的匹配过程如图11所示，从中看到匹配效率得到进一步的提高。