昨天和Mcree来一场痛快淋漓的头脑风暴​！

叶子为什么是绿色的? 聊起一步步到物理是如何接过生物学家的接力棒深入探索：​参考链接：​为什么植物是绿色的？为了减少光合作用中的噪音

为什么眼睛能看到绿叶​？有没有存在一种植物甚至动物肉眼看不见，但摸的到​？散发着不可见光的生物​ — 依达尔文的进化论葫芦画瓢，这是躲避天敌的终极大招啊​！​

大喵点评：在我们给孩子讲授算法之前，是不是看看动物和植物的演进中都暗合哪些算法？

模拟动植物的行为而创造出的算法是最吸引我的 , 已在地球存在上万年的算法默默地指挥着动物的行为，蚁如何寻找食物，如何告诉同伴最短的路径等等; 对生命演化的好奇也是对生命背后的算法好奇。

视频：简单的规则创造出无限可能

参考历史文章的链接： 简单的算法实现：蚂蚁自己的身体构建桥梁

简单动物的行为是机械编程的 破纪录的机器人凸显动物如何擅长跳跃

七个由动物建造的惊人结构

一道2022念蓝桥杯的题目。非常不错的题材！

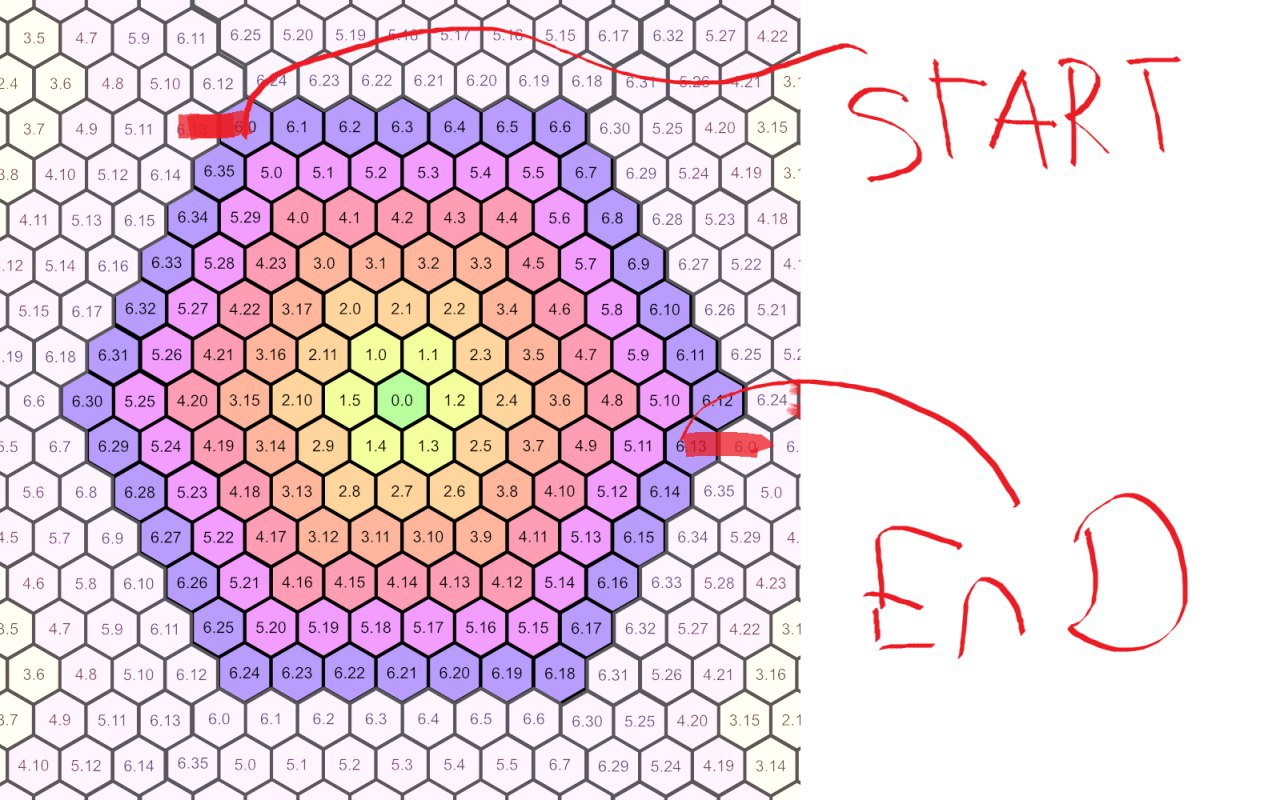
大喵点评：背景取材于游戏中的地图采用的位置表达。

基于蜂窝的位置算法有许多经典的应用场景,主要包括:

1. 游戏地图设计。蜂窝结构的地图可以充分利用空间,方便探索,这很适合许多游戏地图的设计。像roguelike游戏中使用的地下迷宫地图常采用蜂窝结构。

2. 焦点网格。在图像滤波、特征提取等领域,经常使用到焦点网格(focal grid)对图像进行采样。蜂窝结构正好适用于构建焦点网格,可以在图像上均匀离散采样。

3. 蜂窝网络。在移动通信领域,蜂窝网络结构可以在有限空间内提供最大覆盖,这是构建移动网络的一种经典方式。

4. 算法路径搜索。在路径搜索和规划算法中,蜂窝空间结构可以简化空间表示和搜索过程,许多经典算法都在此空间下进行讨论,如A*搜索算法等。

5. 冗余阵列。在存储系统中,蜂窝结构的冗余阵列可以提供均匀的错误检查和纠错能力,如RAID6等技术采用蜂窝阵列结构。

6. 热传导。在许多工程学科中,蜂窝结构都可以均匀有效地传导热量,常被用来设计散热器、换热器等设备。

7. 空间覆盖。需要在平面空间上进行覆盖时,蜂窝结构可以实现最优解,这一特点在encrypt领域得到应用。

8. 图像压缩。图像的频域转换后可以采用蜂窝扫描结构进行编码,这是一种图像压缩编码方式,如蜂窝图像压缩标准等。

所以,总之蜂窝算法在众多领域都找到了成功的应用,主要原因在于它结构简单,既可以在有限空间内高效覆盖,也方便进行空间分割与搜索,这些特性使其成为处理空间信息与问题的一种非常有效的工具。

接下来我们一起探讨这道题。水平所限只是抛砖引玉，直觉有更高效的算法。

以下是蜂窝空间两点最短路径的Python实现:

python的字典 direct定义 6 个方向的解析表达；

字典的value = tuple(x,y)

x = 东西方向的位移；

y = 南北方向的位移；

关键点是我们发现每一步的移动距离在东西方向上的位移大小有两种情形：

这是因为正西0方向和正东3方向时，每一步为 2； 正北和正南方向，每一步为 0；而

1，2，4，5 四个方向移动时，每一步 x 的变换率为 1；

def location(a,b,c):
    direct = {
              0:(-2,0),1:(-1,2),
              2:(1,2), 3:(2,0),
              4:(1,-2),5:(-1,-2)
              }

    #第 1 步完成时的坐标
    x1,y1 = direct.get(a)
    X,Y = b*x1,b*y1

    # 第 2 步完成时的坐标
    x2, y2 = direct.get((a+2)%6)
    X,Y = X + x2*c,Y + y2*c
    return X,Y

#测试用例
a,b,c = 0,5,3
print(location(a,b,c)) #(-7, 6)
a,b,c = 2,3,2
print(location(a,b,c)) #(5, 2)

a,b,c = 0,5,2
print(location(a,b,c)) #(-8, 4)

a,b,c = 2,3,5
print(location(a,b,c)) #(8, -4)

if __name__ == '__main__':
    # 调用函数location和B,C两点参数
    # 由函数返回结果获取B,C的位置坐标
    s,t = location(0,5,0),location(3,3,3)

    # 起点 s和终点 t 的坐标换算为步数
    # 注意 Y 是南北方向移动的步数
    # 首先 Y 条件成立后，再计算 X
    # X=东西方向移动的步数
    
    Y = abs(t[1]-s[1])//2
    X = abs(t[0]-s[0]) - Y * 1
    print(X/2, Y,int(X/2)+Y)

该实现定义了CellularSpace类表示蜂窝空间的坐标计算方法；

并给出shortest_path()方法计算两点最短路径。

即可以改写为函数调用：

def shortest_path(s,t):
    # 调用函数location和B,C两点参数
    # 由函数返回结果获取B,C的位置坐标
    s,t = location(0,5,0),location(3,3,3)

    # 起点 s和终点 t 的坐标换算为步数
    # 注意 Y 是南北方向移动的步数
    # 首先 Y 条件成立后，再计算 X
    # X=东西方向移动的步数
    
    Y = abs(t[1]-s[1])//2
    X = abs(t[0]-s[0]) - Y * 1
    print(X/2, Y,int(X/2)+Y)

实例调用该计算(2, 3)到(8, 12)的最短路径是 7

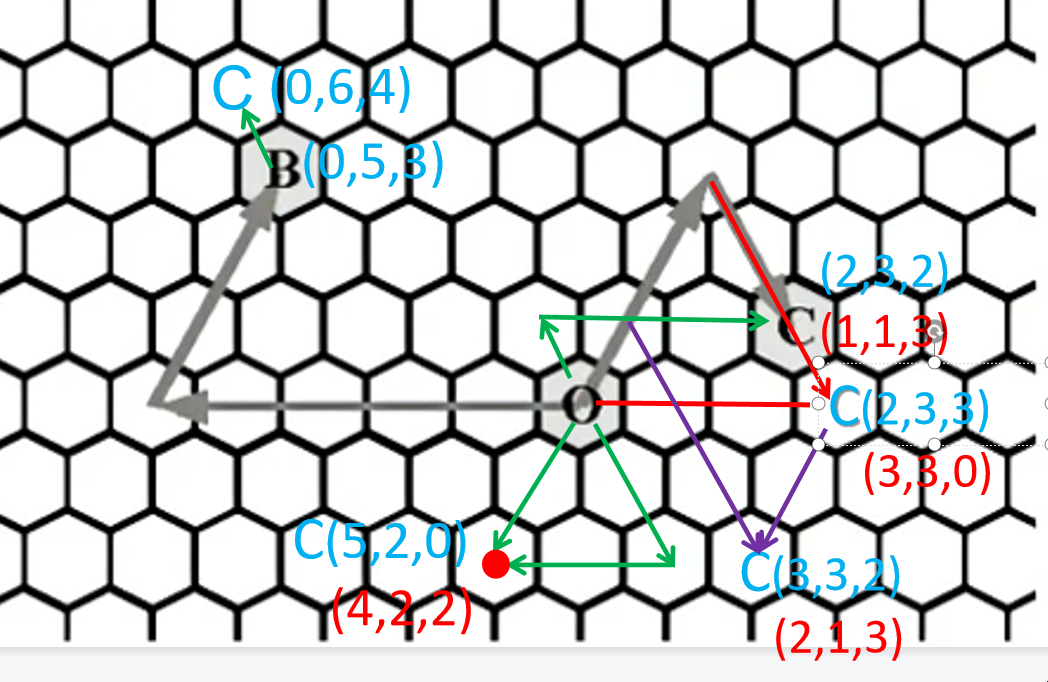
选取 B 附近的点，测试结果正确；

s,t = location(0,5,3),location(0,6,4)
1

选取 C(2,3,2) 附近的点(2,3,3)，又发现该点还可以表达为(3,3,0)

测试结果一致并且正确：

s,t = location(0,5,3),location(2,3,3)
8

s,t = location(0,5,3),location(3,3,0)
8

以上显示结果都是 8 步！

进一步验证。

考虑到同一个位置有不同的表达，例如下图中红色标记的 C 点，有两种甚至更多种路径可以到达：

题目给出的 C(2,3,2) 点还可以表达为(1,1,3)

s,t = location(0,5,3),location(2,3,2)
7

s,t = location(0,5,3),location(1,1,3)
7

输出结果都是 7，B(0,5,3)到C最少步数是 7 步；

再例如：

图中右下角的 C(3,3,2)，又可以表达为 (2,1,4)

输入两种不同的表达，再看是否的同样的结果？

起点选择在 原点 O，分别带入坐标后结果一致：

s,t = location(0,0,0),location(3,3,3)
3

s, t = location(0, 0, 0), location(2, 1, 3)
3

再看左下角的红点：

s,t = location(0,0,0),location(5,2,0)
2

s, t = location(0, 0, 0), location(4, 2, 2)
2

最后测试图中相距最远的两个点： (0,5,3)和 (3,3,2)

s,t = location(0,5,3),location(3,3,2)
8

游戏中采用蜂窝位置算法的主要原因有:

1. 空间利用效率高。蜂窝形状是一种经典的空间填充形状,可以在二维平面上充分利用空间,避免空隙。这在游戏地图等空间受限的场景中很有用。

2. 减少重叠区域。由于蜂窝形状空间填充紧密,使相邻单元之间重叠区域最小。这可以避免在寻找可用空间和判断视野、射程时出现重叠歧义的情况。

3. 方便探索。蜂窝形状空间划分规则精确清晰,游戏角色可以按规则顺利探索空间,不会由于空隙或死路而卡住。这也便于在空间内进行搜索与追踪。

4. 简单的计算。在蜂窝空间内判断距离、邻居等仅需要简单的整数计算,不需要复杂的几何计算。这减少了游戏算法的计算量,提高了运行效率。

5. 美观的形状。蜂窝形状在视觉上给人以整洁、有序的美感。这在游戏视觉效果上产生正面影响,特别适用于加强空间感的游戏场景。

总体来说,蜂窝位置算法由于空间利用率高、避免区域重叠、方便探索、计算简单以及美观的形状等原因,在游戏开发中得到广泛应用。

它不仅提高了游戏性能,也增强了游戏体验。

当然,蜂窝算法也有一定局限,如增加内存占用和限制某些形状的表达等。在具体应用中还需要综合考虑,选择最优的解决方案。

但作为一种典型的空间分割算法,蜂窝位置算法的优点明显大于缺点,这也是它在游戏与图形学领域得到广泛运用的原因。

作为一名数学家、植物生物学家和数据科学家，我经常发现自己想知道为什么我们只有一种众所周知的算法，即神经网络，用于基于细胞的机器学习。

神经元只是一种类型的细胞，还有许多其他类型的细胞执行决策和学习功能。

更好的是，有些植物细胞特别有趣，因为它们是全能的。这意味着每个细胞都有植物的完整遗传信息。

因此，任何细胞都可以经历分化，变成叶子、根、花或干细胞，更令人印象深刻的是，可以从组织培养物中生长出全新的植物。

从表面上看，这似乎无趣或显而易见，但最终在工作中会做出复杂的决策。植物细胞如何知道何时变成叶子、芽、根或全新的植物？

为什么这么小的包不仅包含制定该决定的所有信息，而且还包含做出该决定的所有信息？提出这些问题并尝试以编程方式回答它们可以为机器学习和人工智能提供有趣的新方法。

当我考虑如何像植物细胞一样运作的算法时，我经常发现自己将决策树视为模型集合的第一步，其中决策树将选择应该实现的一个或多个模型。

例如，在某些情况下，当植物经历大量光照、高温和干燥土壤时;营养生长减慢，根系生长增加，现有叶子枯萎。这只是植物根据复杂的环境场景做出复杂决策的众多例子之一（如果您不相信植物会做出决定，请查看此播客）。

现在所有的植物都很酷，但我对一组特别感兴趣;兰花。由于其高度专业化和长寿命，兰花的行为方式令人困惑和迷人（只要问问任何兰花爱好者）。

他们可以选择多年不开花，与真菌建立动态关系，并且已经进化出惊人的特定方式，几乎在世界各地茁壮成长。

兰花是机会主义者和操纵者，通过研究它们可以学到很多东西。

我经常发现自己倾向于我的个人收藏，想知道我是否可以编写一种算法来告诉我如何以最佳方式照顾它们，或者可以帮助我识别它们（由于收敛进化，这很困难），或者更好的算法以某种方式模仿它们采用的机制，但可以应用于其他问题。

神经网络本身就很迷人，并且已经能够做一些令人惊奇的事情，但它们也有局限性，并且计算成本非常高。

我们可以做得更好，可以构建一种像植物细胞一样运作的算法（也许，只是也许，像植物细胞一样，它会更有效率）。