116. 填充每个节点的下一个右侧节点指针

描述

给定一个完美二叉树，其所有叶子节点都在同一层，每个父节点都有两个子节点。二叉树定义如下：

struct Node {
  int val;
  Node *left;
  Node *right;
  Node *next;
}

填充它的每个 next 指针，让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点，则将 next 指针设置为 NULL。

初始状态下，所有 next 指针都被设置为 NULL。

示例

示例1
示例1

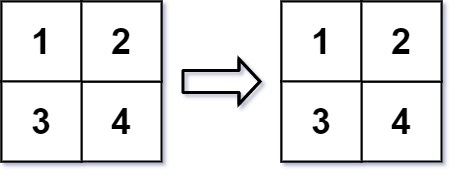
输入：root = [1,2,3,4,5,6,7]
输出：[1,#,2,3,#,4,5,6,7,#]
解释：给定二叉树如图 A 所示，你的函数应该填充它的每个 next 指针，以指向其下一个右侧节点，如图 B 所示。序列化的输出按层序遍历排列，同一层节点由 next 指针连接，‘#’ 标志着每一层的结束。

示例2

输入：root = []
输出：[]

链接

https://leetcode.cn/problems/populating-next-right-pointers-in-each-node/

解题思路

思路一: 广度优先遍历

首先根元素入队
当队列不为空的时候
求当前队列的长度length
依次从队列中取 length个元素进行处理，先取出队列中的第一个节点node，当node不是最后一个时，将node.next指向队列的第一个，然后进入下一次迭代

/**
 * @param {Node} root
 * @return {Node}
 */
var connect = function(root) {
    if (root == null) return root;
    let queue = [root];
    while(queue.length) {
        let len = queue.length;
        for (let i = 0; i < len; i++) {
            let node = queue.shift();
            if (i < len - 1) {
                node.next = queue[0];
            } 
            node.left && queue.push(node.left);
            node.right && queue.push(node.right);
        }  
    }
    return root;
};

时间复杂度： O(n), 其中 n 是二叉树的节点数
空间复杂度： O(n)

思路二: 使用已建立的 next 指针

分为两种情况：

两个子节点属于同一个父节点，则node.left.next = node.right;
不同父节点之间子节点, 由于已经在父节点这一层建立了 next 指针，因此可以直接通过第一个父节点的
next 指针找到第二个父节点, 然后在它们的孩子之间建立连接, node.right.next = node.next.left;

实现代码如下：

/**
 * @param {Node} root
 * @return {Node}
 */ 
var connect = function(root) {
    if (root === null) return root; 
    let leftNode = root;
    while (leftNode.left != null) {
        let head = leftNode;
        while (head != null) {
            // 两个子节点属于同一个父节点
            head.left.next = head.right;
            if (head.next != null) {
                // 不同父节点之间子节点
                head.right.next = head.next.left;
            }
            // 指针向后移动
            head = head.next;
        }
        // 去下一层的最左的节点
        leftNode = leftNode.left;
    }
    return root;
}