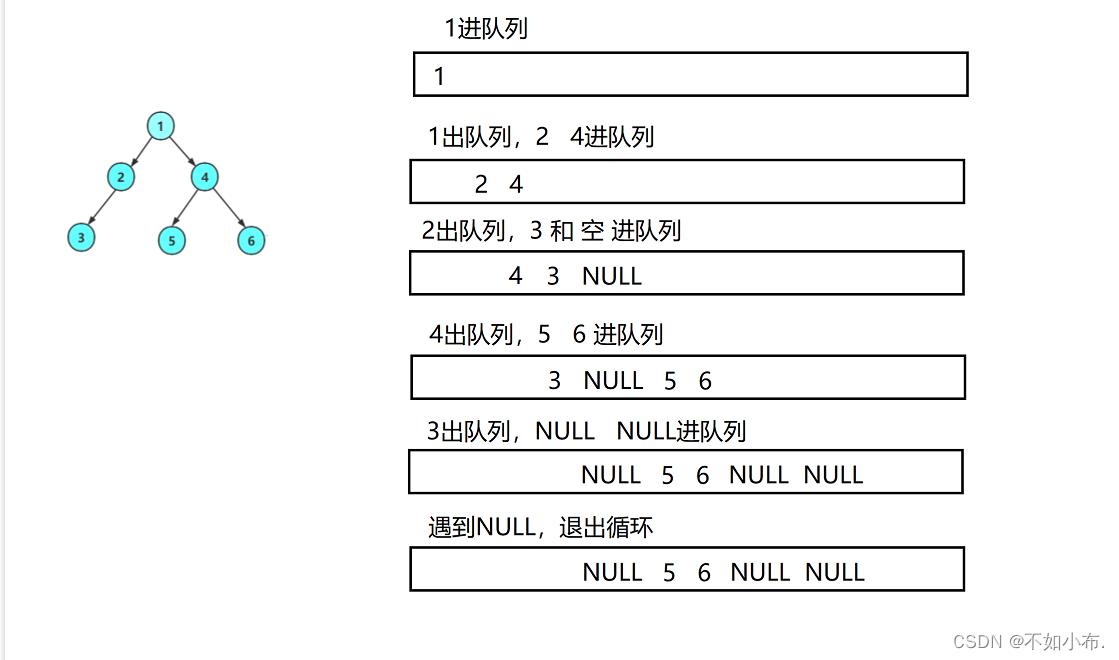
给定一个二进制字符串 s 和一个正整数 n，如果对于 [1, n] 范围内的每个整数，其二进制表示都是 s 的 子字符串 ，就返回 true，否则返回 false 。

子字符串 是字符串中连续的字符序列。

示例 1：

输入：s = "0110", n = 3
输出：true
示例 2：

输入：s = "0110", n = 4
输出：false
 

提示：

1 <= s.length <= 1000
s[i] 不是 '0' 就是 '1'
1 <= n <= 109
链接：https://leetcode.cn/problems/binary-string-with-substrings-representing-1-to-n

解一:暴力(bitset模板)

class Solution {
public:
    bool queryString(string s, int n) 
    {
        for(int i = 1;i <= n; i++)
        {
            auto str = bitset<32>(i).to_string();
            str = str.substr(str.find('1'));
            if(s.find(str) == s.npos)return false;
        }
        return true;
    }
};

解二:哈希表

以下代码请自行理解,可以自己写一个小的二进制串跟一遍

class Solution {
public:
    bool queryString(string s, int n)
    {
        unordered_set<int>ans;
        for(int i = 0;i < s.size(); i++)
        {
            int x = s[i] ^ 48;
            if(!x)continue;
            for(int j = i + 1;x <= n;j++)
            {//提问1:为什么是j = i + 1 ??? 
                ans.insert(x);
                x = (x << 1) | (s[j] ^ 48);//提问二:这样赋值的意义?
                if(j == s.size() )break;
            }
        }
        return ans.size() == n;
    }
};

解三:滑动窗口 + 哈希表 + 数学

分析:

1:列表

1	1
2	10
3	11
4	100
5	101
6	110
7	111
8	1000
9	1001
10	1010
11	1011
12	1100
13	1101
14	1110
15	1111

总结:

直接分享这位大佬的题解,讲的很详细也很全面

 

根据上列三个

class Solution {
public:
    bool help(const string& s, int bitlen, int min, int max) 
    {
        unordered_set<int> st;
        int t = 0;
        for (int r = 0; r < s.size(); ++r)
        {
            t = (t << 1) + (s[r] ^ 48);
            if (r >= bitlen)
                t -= (s[r - bitlen] ^ 48) << bitlen;
            if (r >= bitlen - 1 && t >= min && t <= max)
                st.insert(t);
        }
        return st.size() == max - min + 1;
    }

    bool queryString(string s, int n) 
    {
        if (n == 1)  return s.find('1') != s.npos;
        int bitlen = 31 - __builtin_clz(n);
        if (s.size() < (1 << (bitlen - 1)) + bitlen - 1 || s.size() < n - (1 << bitlen) + bitlen + 1) return false;
        return help(s, bitlen, 1 << (bitlen - 1), (1 << bitlen) - 1) && help(s, bitlen + 1, 1 << bitlen, n);
    }
};