---

第五章 树与二叉树

小题考频：30
大题考频：8

---

5.5 树与二叉树的应用

难度：☆☆☆☆

知识总览

5.5.1 哈夫曼树

5.5.2_1 并查集

5.5.2_2 并查集的进一步优化

——补充：并查集的终极优化

---

5.5.1 哈夫曼树

带权路径长度

带权路径长度：边数✖结点上的权值
Eg.

树的带权路径长度：所有的叶子结点带权路径长度之和（WPL）

哈夫曼树的定义

只算叶子结点，带权路径长度之和
哈夫曼树WPL最小，也称最优二叉树
上图中中间两棵树的WPL=25为最小，那么这两棵树即哈夫曼树。

哈夫曼树的构造

1. 选权值最小的两个结点让他们成为兄弟。
   Eg. 选a结点和c结点
2. 把这两个结点的权值之和作为新树根结点的权值，然后继续选。
   Eg.新树为权值为3，选新树和e

重复上述操作。

哈夫曼树的一些性质：

1. 每个初始结点最终都成为叶结点，且权值越小的结点到根结点的路径长度越大
2. 两两结合需要进行n-1次，每结合一次会增加一个分支结点，哈夫曼树的结点总数为2n-1
3. 哈夫曼树中不存在度为1的结点。
4. 哈夫曼树并不唯一，但是WPL相同且最优。

Eg.2 另一种构造方法：

哈夫曼树的特性有什么用呢？

---

哈夫曼编码

发电报——点、划两个信号（二进制0/1）

如果采用ASCII编码，两人想传递100个答案，就需要操作8×100=800次，显然不高效。
字符集中只有四个字符，用两个二进制位就可以区分出四种状态：
也属于固定长度编码，每个字符的二进制位长度相同。

80个C、10个A、8个B、2个D，可以映射成树，向左走是0，向右走是1：

那么所有答案的二进制长度就是最终的WPL=200，即操作200次就可以把答案传出去。

有没有更好的方案？
也就是说，让他们之间传递的二进制比特信息尽可能的少。
即构造的编码树的带权路径长度尽可能的小。

即构造哈夫曼树：

权值最小的是D和B，让其合并，接下来是A，最后是C

也就是说只要操作130次，就可以把答案传递出去了。

此处各字符对应的二进制长度不相同，这种编码方式就叫可变长度编码。

Q：此处不就是想用四个二进制串，来区分四个字符吗？字符A出现的频率也高，为什么非要用两个二进制位来表示A，而不用1来表示呢？这样也可以保证四个字符的二进制编码不一样。

A：用1来表示A，在树的形式中，A就变成了一个非叶子结点：

此时想要传递 CAAABD答案，就变成了0 111 111 110，接受这一段二进制数之后，要把信息翻译成A、B、C、D，就会变成C(0)、B(111)、B(111)、D(110)，那么就出现了歧义：

如果用左边的编码方案，可以得到正确结果：

左边这种编码方式可以称为：前缀编码

任何一个编码都不是另一个编码的前缀——无歧义

有哈夫曼树得到哈夫曼编码——字符集中的每个字符作为一个叶子结点，各个字符出现的频度作为结点的权值，根据之前介绍的方法构造哈夫曼树

因为哈夫曼树并不唯一，所以哈夫曼编码也不唯一

---

应用：英文字母频次

注：不可以传答案！

---

5.5.2_1 并查集

漏网之鱼：逻辑结构——“集合”

补一下没学过的集合，在数学里很常用

可以将所有元素划分为几个子集：

那么，在集合的关系之下，任意挑选出两个元素，两个元素间有什么关系呢？

A和H不属于同一个集合
A和E属于同一个集合

回顾：森林

也可以用树、森林这种表示方式来表达出各个元素之间的

把属于同一个集合的元素组织成一棵树，不同集合的元素放到不同的树里。

用互不相交的树，表示多个“集合”：

“查”：指定一个元素，判断到底属于哪一个集合
——从指定元素出发，一路向北，找到根结点，通过根结点判断属于哪个集合
如何判断两个元素是否属于同一个集合？
——分别查到两个元素的根，判断根结点是否相同即可，根结点不一样就是从属于不同的两个集合

“并”：把两个合集合并为一个合集
——让一棵树成为另一棵树的子树即可

并查集，本质上是表示一种集合的逻辑关系，对这个集合需要实现的基本操作就是并和查。

用双亲表示法。

---

回忆：树的存储——双亲表示法

根结点A没有父结点，对应的数组元素是-1；
G这个结点在数组里的位置是6，其父结点是C，C的位置在数组里是2，那么G对应的数据元素就是2指向C的下标。
用一个静态数组描述出各个结点之间的父子关系，方法就是让孩子结点的元素指针指向其父结点所对应的数组下标。
这些指针都是往上指的，给定一个结点要找到结点的父结点，或者一路往上找到其根结点就会很容易。并且想让两棵树并为同一棵树，只需要让一棵树的根结点的parent指向另一棵树的根结点的编号。

使用双亲表示法，并和查这两个操作实现起来都会非常方便。

查：找根结点；并：找一棵树的根结点指向另一棵树的根结点

---

“并查集”的存储结构

将刚才提到例子中的ABCD……M，分别给他们对应上一个静态的数组元素。

L结点数组下标为11，父结点是E结点数组下标为4，所以和L对应的数组元素S[ ]就是4：
E的父结点是B，B的下标是1，那么E对应值为1：
B的父结点是A，A的下标是0，那么B对应值为0：
A是根，对应数组元素的值是-1

对于其他两棵树也以此类推。

总结并查集：
Q：对于n个数据元素，如何表示这些数据元素之间的集合关系，属于同一集合还是不同集合？
A：声明一个长度为n的int型数组S，用这个数组表示它们的集合关系，本质上就是树的双亲表示法。

---

“并查集”的基本操作

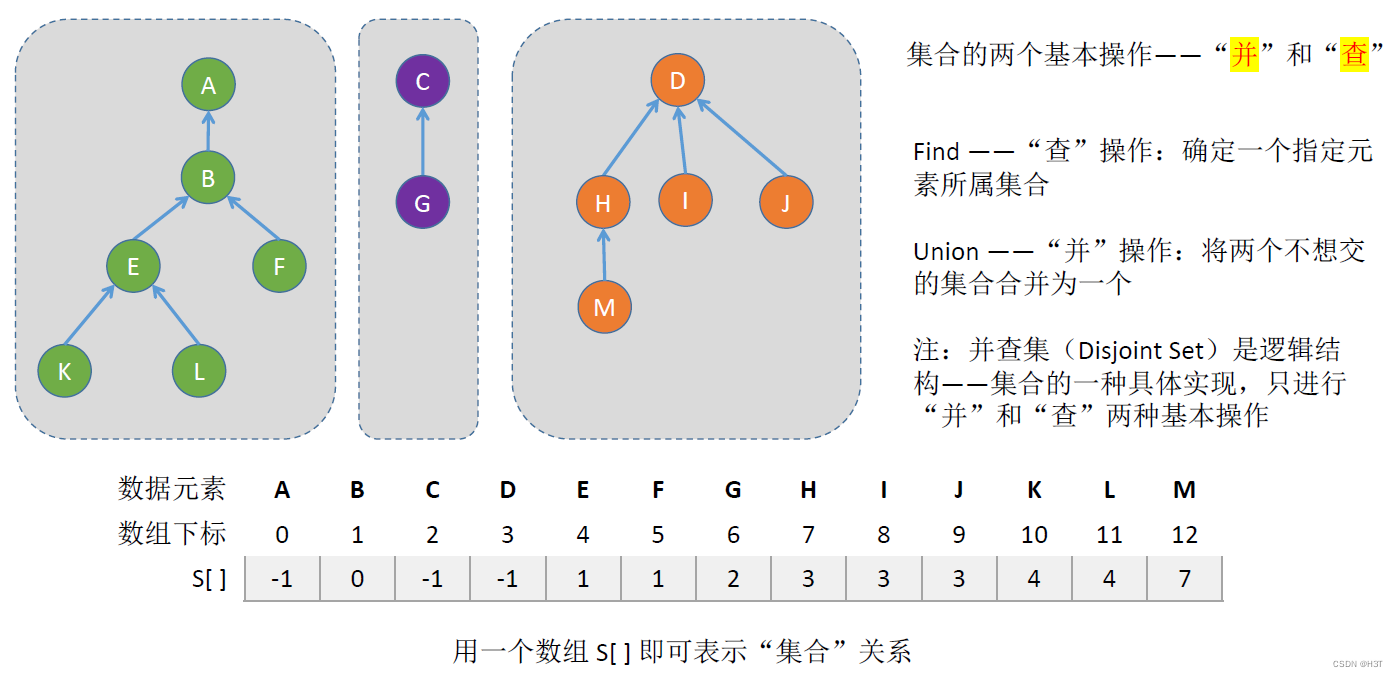
查：确定指定元素所属集合
——利用数组一路往上找到根结点
并：合并两个不相交的集合
——让一棵树的根结点所对应的数组的值指向另一棵树的下标

并查集（Disjoint Set）是逻辑结构——集合的一种具体实现，只进行“并”和“查”两种基本操作

---

“并查集”的代码实现——初始化

用一个int型的数组来表示刚开始的这些元素，此时并不知道这些元素到底是否属于同一个集合，可以初始化为各自独立的n个子集，所以初始化并查集时，将所有数组的元素数组的值全部赋值为-1。

表示每个元素之间是各成一派的，每个元素就是独立的一个子集。

初始化之后，就可以根据实际的业务需求来对各个元素，各个集合进行合并，如果两个元素应该划分到同一个子集，那么就把它们并到一起。

---

“并查集”的代码实现——并、查

Find操作：找L结点所属集合，用while循环，L是11号，指向4号E结点，指向1号B结点，指向0号A结点，A指向-1，为根结点，那么L就属于A统治的子集。

Union操作：要把绿色和紫色两个集合合并为一个，两个子集的根结点分别为A、C，即传入A和C的数组下标0和2，先判断当前要合并的两个集合是两个不同的集合（相同直接return），然后将一个根结点的数组指针指向另一个根结点，S[2] = 0，这个操作就让C连到A结点下。

Eg. 合并E和G结点：先对它们进行find，找到它们的根结点分别是哪个，然后对根结点进行Union操作合并。

---

时间复杂度分析

并：把两个根结点合并，时间复杂度：$O(1)$

查：查J。左边情况下，查1次（较好的情况）；右边情况下，查n次【最坏的情况和树的高度h相关】，时间复杂度$O(n)$

想要优化并查集的效率，那么就要在构造树的时候，让树的高度h尽量低！

---

Union操作的优化

是否可以让较小的树合并到较大的树呢？

1. 如果大树合并到小树：
   

树的高度增加了

2. 让小树合并到大树：
   

树的高度没有变化

思路：每一次Union都让小树合并到大树上，用根节点的绝对值表示树的结点总数：

A的值是-6，绝对值为6，代表树有6个结点；
C的值是-2，绝对值为2，代表树有2个结点；
D的值是-5，绝对值为5，代表树有5个结点；
结点总数少的树为小树，让小树的根结点的值指向大树的根结点，并更新大树的结点树，如C合并到A，A的值更新为-8

步骤：
首先判断这两棵树，哪棵更小（由于是负值，负值越大，绝对值越小，结点越少，是小树），C结点更小，要将C结点合并到A结点；
累加结点总数，把-2和-6进行相加；
把更小的树的根结点C指向更大的树的根结点，将S[2] = 0

再合并另外两棵树：

可以发现，通过小树合并到大树，树的高度并没有变化。

对Union进行优化后，树的高度不会超过$[lo{g}_{2}n]+1$
Find操作的最坏时间复杂度为：$O(lo{g}_{2}n)$

---

5.5.2_2 并查集的进一步优化

——补充：并查集的终极优化

拓展：Find 操作的优化（压缩路径）

要找结点L所属集合，从L出发到E到B到A，这条路径称为查找路径。

压缩路径——Find操作，先找到根节点，再将查找路径上所有结点都挂到根结点下：

A为根结点，从L出发可以一次查找这条查找路径上的各个结点，此时需要把查找路径上的结点全都挂到根结点A下面。

把L挂到A下

把E挂到A下

此时查找L只需要一次操作，也就是说查找L的路径长度就被压缩了。

给出指定x，找到x所属的根；
向上找到查找路径上的结点，挂到根结点下；

每次Find操作，先找根，再“压缩路径”，可使树的高度不超过𝑂(α(𝑛))。α(𝑛)是一个增长很缓慢的函数，对于常见的n值，通常α(𝑛)≤4，因此优化后并查集的Find、Union操作时间开销都很低

时间复杂度甚至可以$\le O(4)$

并查集的优化

Union优化思路：小树合并到大树，时间复杂度不超过$O(lo{g}_{2}n)$
Find优化：先找到根节点，再进行“压缩路径”
核心思想：尽可能让树变矮

合并n个独立元素，需要进行n-1次的Union，每次都需要进行Find操作，所以取决于Find操作的时间复杂度（树高h）。

快乐时刻

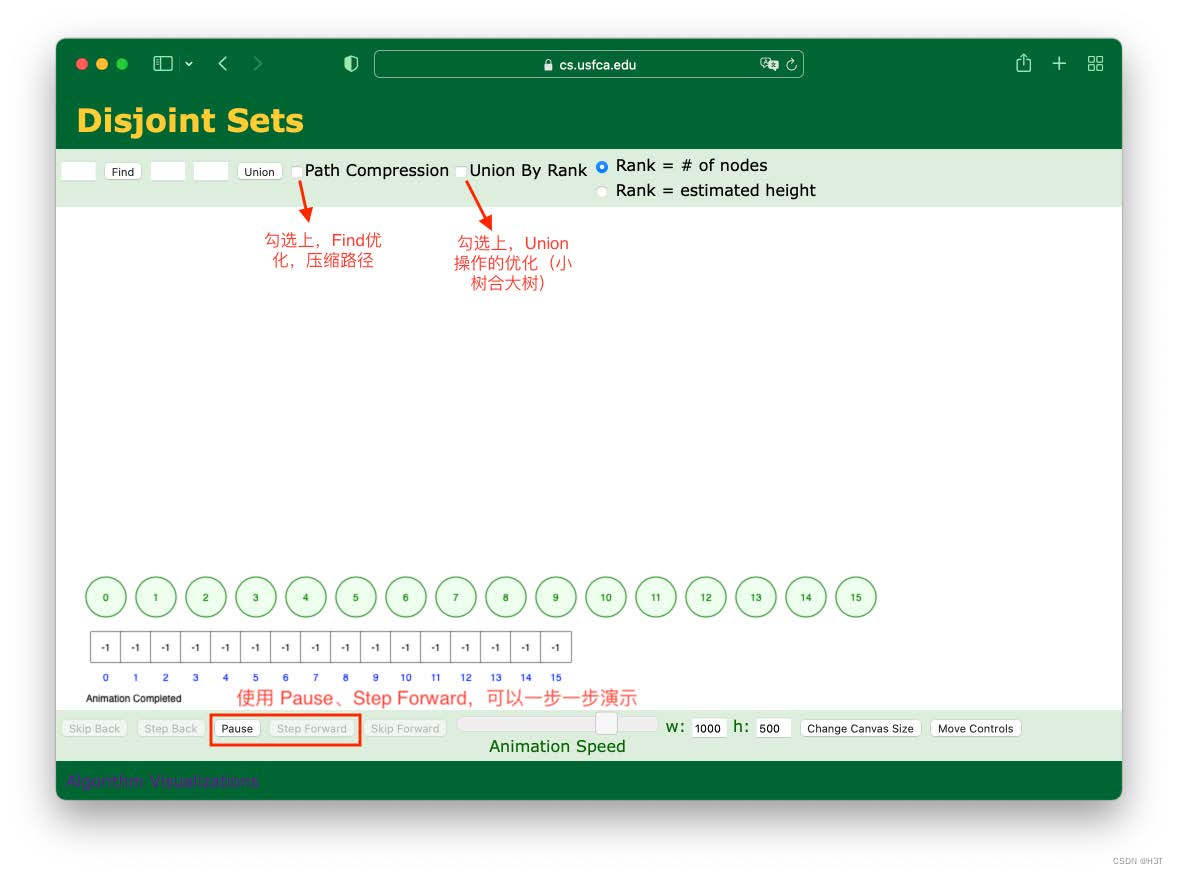
可以体验模拟并查集算法
https://www.cs.usfca.edu/~galles/visualization/DisjointSets.html

以及各种算法
https://www.cs.usfca.edu/~galles/visualization/Algorithms.html

---

知识回顾与重要考点

5.5.1 哈夫曼树

• 树的带权路径长度（WPL）
• 哈夫曼树
• 构造哈夫曼树
• 哈夫曼编发：可用于数据压缩

---

5.5.2_1 并查集

• Union操作时，让小树并入大树
• 优化后，树高≤$[lo{g}_{2}n]+1$
  Find -> $O(lo{g}_{2}n)$

---

5.5.2_2 并查集的进一步优化

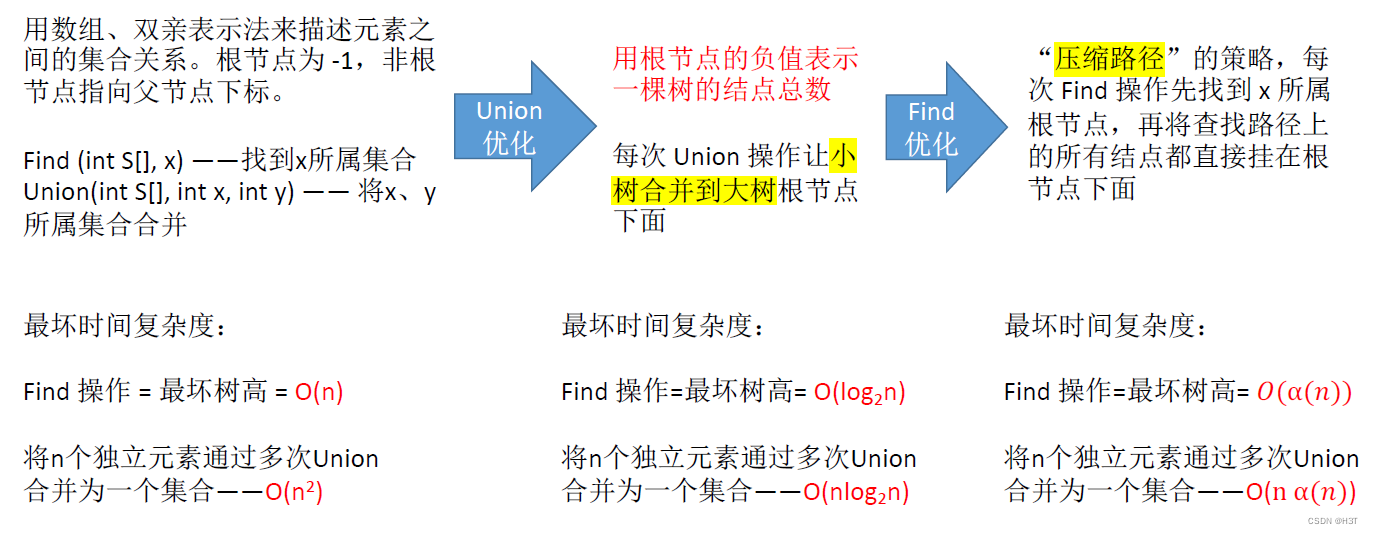
合并n个独立元素，需要进行n-1次的Union，每次都需要进行Find操作，所以取决于Find操作的时间复杂度（树高h）。