一、连续系统的频域分析

一个系统的重要指标就是求系统函数，用系统函数来表征这个系统得特性，系统函数其实系统对外的一个信号处理的特性表达式而已。

1. 系统函数与系统的频域分析

1. 理论分析

对于一个 LTI 系统，常用的数学描述模型是线性常系数微分方程，其一般形式为

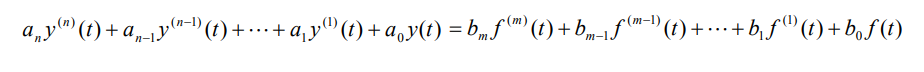
对微分方程两边同时取傅立叶变换

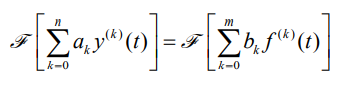
根据傅里叶变换的线性特性（把系数分离嘛）

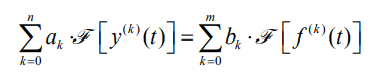
再根据傅里叶变换的时域微分特性（傅里叶变换的性质）

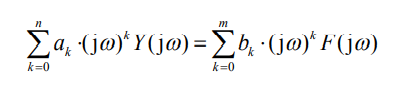
将上式中的Y(jω) / F(jω) 整理，将其定义为 H(jω)，其实和时域的系统函数一样。

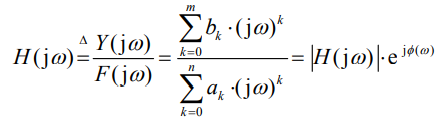
其中， H(jω)称为连续系统的系统函数，也叫系统的频率响应。 H(jω) 是系统函数的幅频特性，φ(jω)是相频特性。
系统函数与系统的冲激响应的关系为：

2. 频域分析法求解系统零状态响应步骤

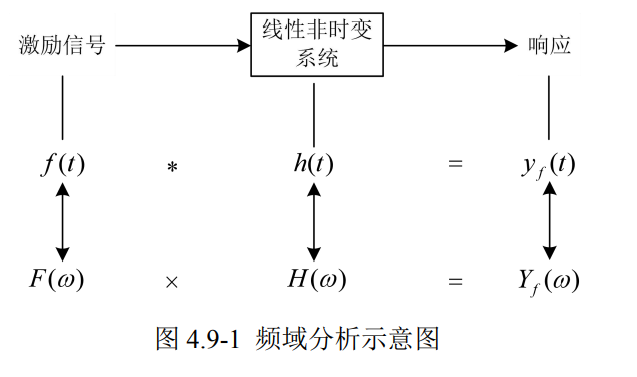
• 第一步：求输入信号 f (t)的傅里叶变换 F(jω) ；
• 第二步：求系统函数 H(jω)；
• 第三步：求零状态响应 y_f(t) 的傅里叶变换 Y_f(jω) = F(jω) · H(jω)
• 第四步：求Y_f(jω)的傅里叶逆变换，即得
  

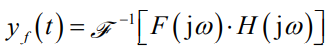
示意图：

例题：

2. 无失真传输

一般情况下，系统的响应波形与激励波形不相同，信号在传输过程中将产生失真。
线性系统引起的信号失真由两方面因素造成

• 一是系统对信号中各频率分量幅度产生不同程度的衰减，使响应各频率分量的相对幅度产生变化，引起幅度失真。
• 二是系统对各频率分量产生的相移不与频率成正比，使响应的各频率分量在时间轴上的相对位置产生变化，引起相位失真。

必须指出，线性系统的幅度失真与相位失真都不产生新的频率分量。而对于非线性系统则由于对传输信号产生非线性失真，可能产生新的频率分量。这里只记录有关线性系统的幅度失真和相位失真问题。

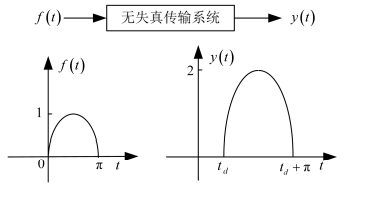
所谓无失真是指响应信号与激励信号相比，只是大小与出现的时间不同，而无波形上的变化。

要使信号 f (t)无失真地传输，在时域上响应 y(t) 与激励信号 f (t) 之间应满足

• y(t) = Kf (t - t_d)
  幅度增益 K 及延迟时间 t_d 均为常数。它表示输出信号在幅度上比 f (t)增大了 K倍（当0 < K <1时，幅度实际是压缩了），在时间上滞后了 t_d 秒，而波形未发生畸变，因而为不失真。

我们换到频域看 ，对 上面的 y(t) = Kf (t - t_d) 两边傅里叶变换

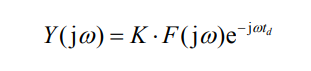
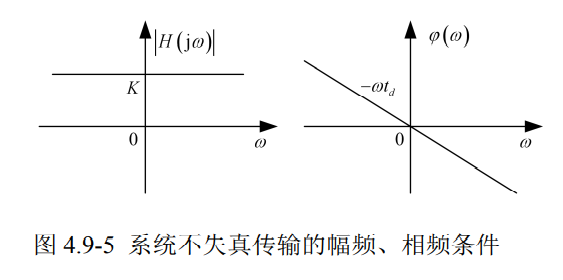
因而信号在系统中无失真传输的幅频条件和相频条件为

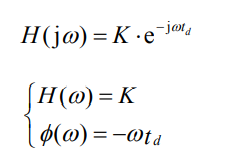
欲使信号通过线性系统不失真传输，应使系统函数的模值为一常数，而相位特性为过原点的直线