一.递归

1.什么是递归

递归是一种编程技术，它通过在函数内部反复调用自身来解决问题。当一个程序调用自己时，这就称为递归调用。递归可以有助于简化某些算法的实现和理解。在递归过程中，每个调用都会将一些数据保存在栈上，直到递归结束后才能被处理并弹出栈。

递归通常有两个部分：基本情况和递归情况。基本情况是在函数执行之前判断是否需要递归，如果不需要，则直接返回结果。递归情况是函数需要递归时，它会调用自身，但是传入的参数通常会有所不同，以便最终能够达到基本情况而结束递归。

虽然递归可以使代码更加简洁，但是需要注意的是，在一些情况下，它可能会导致性能问题或者栈溢出等问题。因此，在编写递归代码时，需要仔细考虑算法的边界条件和递归深度等因素。

2.递归函数

递归函数是一种函数，它在其定义中调用自身。通常情况下，递归函数包含两个部分：基本情况和递归情况。

基本情况是指在递归函数中需要判断是否需要终止递归的条件。当满足这个条件时，递归就会停止。

递归情况是指在递归函数中需要调用自身的情况。在每次调用时，函数的参数都应该有所不同，以便最终能够达到基本情况而停止递归。

递归函数通常用于处理树形结构、图形结构或其他类型的嵌套结构数据。例如，在二叉树中查找某一个值，就可以使用递归函数来实现。

3.说明

虽然递归算法比较简单，但是它是一种编程的思想，在解决部分问题时，它非常适用。并且他一般作为一种工具，搭配其他思想一起使用。它是C语言数据结构与算法中最简单的算法，这里举几个例子来学会使用它。

二.斐波那契数列

1.问题描述

斐波那契数列是一个经典的数学问题，由0和1开始，之后的每一项都是其前面两项的和。也就是说，斐波那契数列的前几个数是：0、1、1、2、3、5、8、13、21、34……依次类推。

斐波那契数列在自然界中有很多应用，比如植物的叶子排列、蜂窝的构造等等。除此之外，在计算机科学领域内，斐波那契数列也有着广泛的应用，例如在排序算法、密码学等领域。

斐波那契数列的通项公式是：F(n) = F(n-1) + F(n-2)，其中F(0)=0，F(1)=1。根据这个公式可以使用递归函数或循环语句来实现求斐波那契数列的第n项。

2.思路

像这种可以求出通项公式的数列是我们平时典型的递归函数运用，通项公式可以定义为函数，它的第一个值一般是我们的递归函数出口。所谓递归函数的出口就是结束递归的标志。

现在理清思路后，我们来用代码完成求斐波拉契数列的第n项：

3.C语言代码

#include <stdio.h>

int fibonacci(int n) {
    if (n == 0)
        return 0;
    else if (n == 1)
        return 1;
    else
        return fibonacci(n - 1) + fibonacci(n - 2);
}

int main() {
    int num, i;
    printf("Enter the number of terms: ");
    scanf("%d", &num);
    printf("Fibonacci series terms are:\n");
    for (i = 0; i < num; i++) {
        printf("%d ", fibonacci(i));
    }
    printf("\n");
    return 0;
}

三.汉诺塔

1.问题描述

该问题的主要材料包括三根高度相同的柱子和一些大小及颜色不同的圆盘，三根柱子分别为起始柱A，辅助柱B及目标柱C。

**操作规则：**每次只能移动一个盘子，并且在移动过程中三根杆上都始终保持大盘在下，小盘在上，操作过程中盘子可以置于任意杆上。

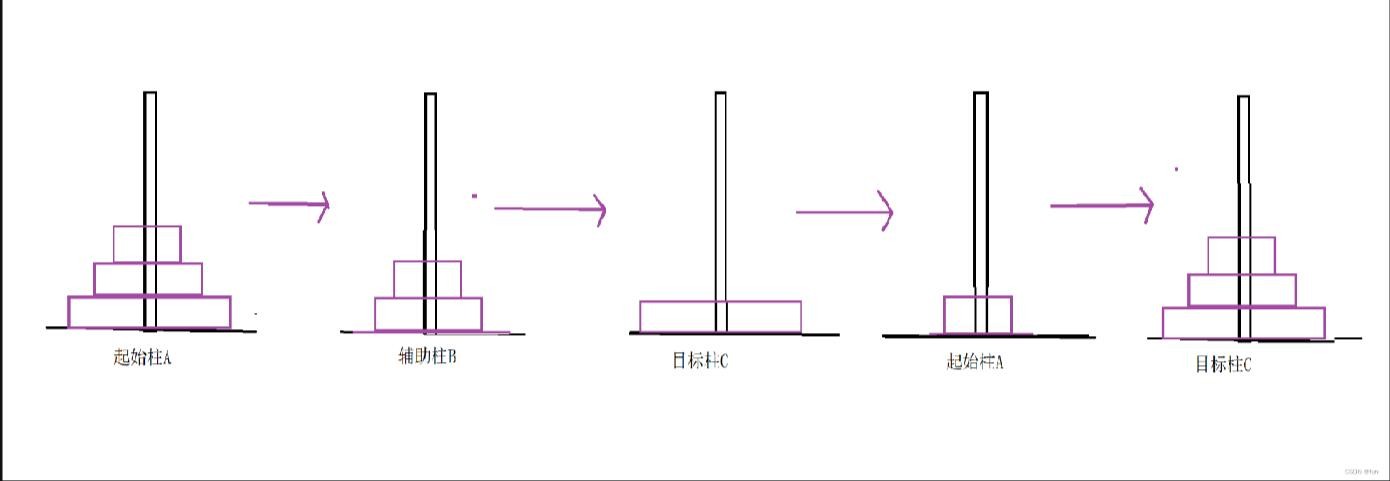
2.分析

汉诺塔是一种经典的递归问题，它涉及到将一组不同大小的圆盘从一个柱子移动到另一个柱子。以下是汉诺塔的具体过程：

将所有圆盘从起始柱子上除最下面一个圆盘之外的其他圆盘全部移动到中间柱子。
将最下面的圆盘从起始柱子上移动到目标柱子上。
将中间柱子上除了最下面的圆盘之外的其他圆盘全部移动到目标柱子上。

在完成这三个步骤时，需要遵守以下规则：

一次只能移动一个圆盘。
大圆盘不能放在小圆盘上面。

通过递归调用上述步骤，可以将所有的圆盘从起始柱子移动到目标柱子。由于每次递归都会将一个圆盘从起始柱子移动到目标柱子，因此每个圆盘最多只会被移动一次，所以总共需要移动2^n - 1 次（n 表示圆盘的数量）。

3.C语言代码

#include <stdio.h>

void hanoi(int n, char A, char B, char C) {
    if (n == 1) {
        printf("Move disk 1 from %c to %c\n", A, C);
    } else {
        hanoi(n-1, A, C, B);
        printf("Move disk %d from %c to %c\n", n, A, C);
        hanoi(n-1, B, A, C);
    }
}

int main() {
    int n = 3; // 将3个盘子从A移动到C
    hanoi(n, 'A', 'B', 'C');
    return 0;
}

四.子集问题

1.问题描述

子集问题（Subset）：给定一个含有n个元素的集合S，求出S的所有子集。可以使用递归实现。

2.思路分析

子集问题是一个基本的组合问题，它涉及到从一个给定的集合中选择一些元素组成新的集合。这个问题在计算机科学和数学中非常常见，解决子集问题可以帮助我们更好地理解组合问题和算法设计。

下面是一个简单的思路分析：

首先，我们需要确定如何表示集合。在大多数编程语言中，集合通常是用数组或列表来表示的。
接着，我们需要考虑如何生成所有可能的子集。一种常见的方法是使用递归算法。
对于递归算法，我们需要考虑以下几点：

a. 基本情况：当集合为空时，只有一个空集。

b. 递归情况：对于非空集合，我们可以选择将第一个元素包含在子集中或者不包含在子集中，然后对剩余的元素进行递归处理。
在递归过程中，我们需要维护一个当前子集的列表，并在每次递归结束后将其添加到结果集合中。
最后，我们可以返回结果集合，其中包含了原始集合的所有可能子集。

需要注意的是，由于子集问题的解空间非常大，因此在实际应用中，需要根据具体的场景进行优化，以减少时间和空间复杂度。

3.C语言代码

下面是一个使用C语言递归实现子集问题的示例代码：

#include <stdio.h>

void subset(int set[], int subset[], int n, int k, int start, int curr){
    if (curr == k) {
        printf("{");
        for (int i = 0; i < k; i++) {
            printf("%d ", subset[i]);
        }
        printf("}\n");
        return;
    }
    for (int i = start; i < n; i++){
        subset[curr] = set[i];
        subset(set, subset, n, k, i+1, curr+1);
    }
}

int main() {
    int set[] = {1, 2, 3};
    int n = sizeof(set)/sizeof(set[0]);
    int subset[n];
    for (int i = 0; i <= n; i++) {
        subset(set, subset, n, i, 0, 0);
    }
    return 0;
}

该代码中，subset函数使用了递归实现。其中，set表示原始集合，subset表示当前子集，n表示原始集合的大小，k表示当前子集的大小，start表示遍历起始位置，curr表示当前子集中元素的个数。

在函数中，首先判断当前子集是否已达到目标大小 k，如果已经达到则输出该子集，并返回上一层递归。否则，从遍历起始位置开始循环原始集合，将元素依次加入当前子集，并对剩余元素进行递归处理。

在 main 函数中，我们遍历所有可能的子集大小，并调用 subset 函数进行求解。最终结果会依次输出到标准输出。

五.归并排序

1.问题描述与分析

归并排序（Merge Sort）是一种基于分治思想的高效排序算法，通过将待排序数组递归地拆分为两个子数组，对每个子数组进行排序，然后将两个有序的子数组合并成一个有序的数组，最终得到排序完成的整个数组。

具体而言，归并排序的过程可以分为三个步骤：

分割：将待排序数组从中间位置划分为左右两个子数组，递归地对左右两个子数组进行分割，直到每个子数组只包含一个元素。
归并：将两个有序的子数组合并成一个有序的数组，直到所有子数组都被合并为一个完整的有序数组。
返回：返回排序完成的数组。

2.C语言代码

下面是用 C 语言递归实现归并排序的代码：

#include <stdio.h>
#include <stdlib.h>

void merge(int *arr, int l, int m, int r) {
    int i, j, k;
    int n1 = m - l + 1;
    int n2 = r - m;

    int L[n1], R[n2];

    for (i = 0; i < n1; i++)
        L[i] = arr[l + i];
    for (j = 0; j < n2; j++)
        R[j] = arr[m + 1 + j];

    i = 0;
    j = 0;
    k = l;
    while (i < n1 && j < n2) {
        if (L[i] <= R[j]) {
            arr[k] = L[i];
            i++;
        } else {
            arr[k] = R[j];
            j++;
        }
        k++;
    }

    while (i < n1) {
        arr[k] = L[i];
        i++;
        k++;
    }

    while (j < n2) {
        arr[k] = R[j];
        j++;
        k++;
    }
}

void mergeSort(int *arr, int l, int r) {
    if (l < r) {
        int m = l + (r - l) / 2;

        mergeSort(arr, l, m);
        mergeSort(arr, m + 1, r);

        merge(arr, l, m, r);
    }
}

int main() {
    int arr[] = {38, 27, 43, 3, 9, 82, 10};
    int n = sizeof(arr) / sizeof(arr[0]);
    
    mergeSort(arr, 0, n - 1);

    for (int i = 0; i < n; i++)
        printf("%d ", arr[i]);
    
    return 0;
}