2023年的深度学习入门指南(14) - 不能只关注模型代码

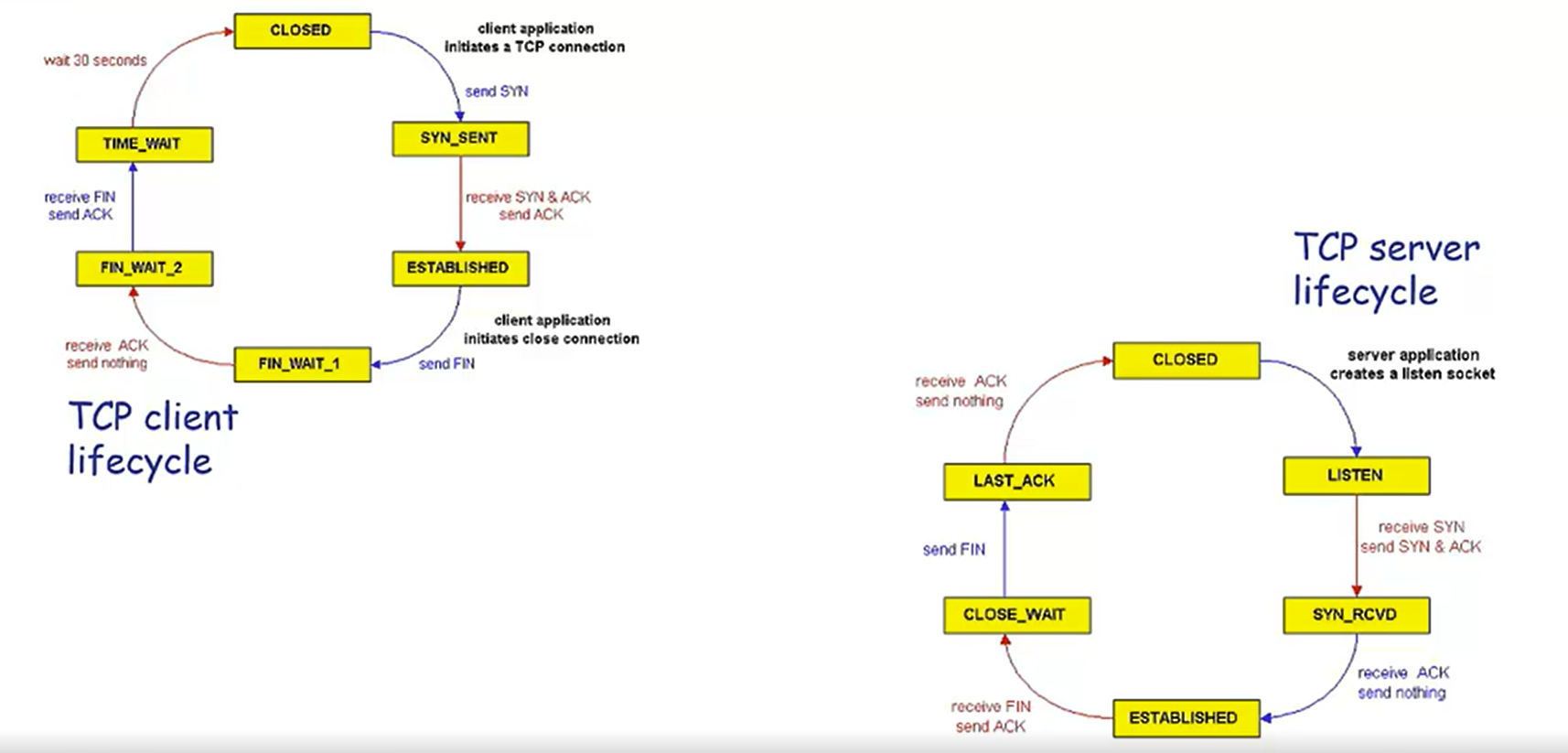
最近，有一张大模型的发展树非常流行：

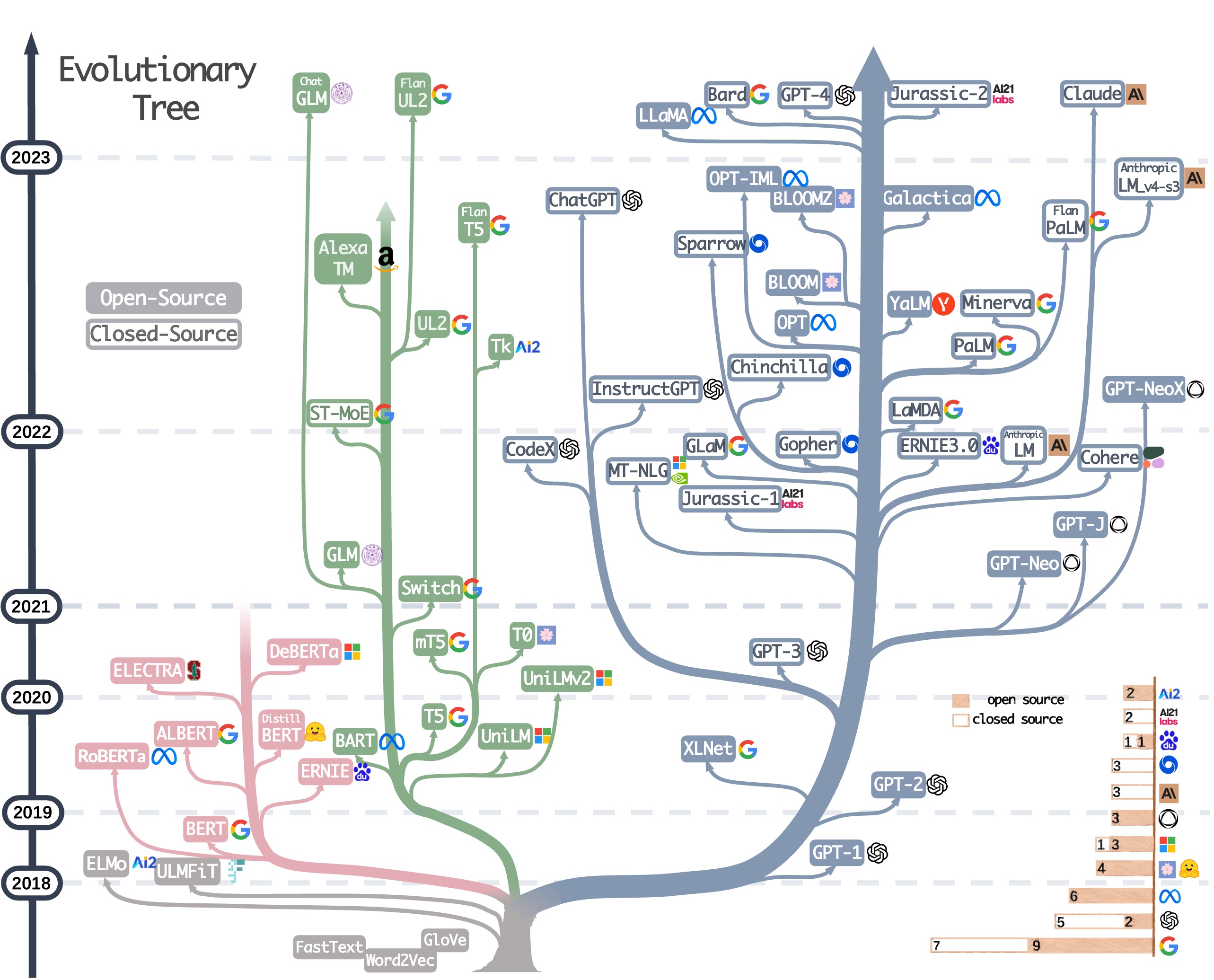
这个图是相当不错的，对于加深对于Transformer模型编码器、解码器作用的理解，模型的开源和闭源情况等等都相当有帮助，大家使用Hugging Face库的时候，也可以从这张图入手寻找相应的模型。

但是，这篇论文是分为三部分的，除了模型之外，还有数据和下游任务两部分。它们被忽视的重要原因是没有一张像上面一样的图。

而且，即使是在图上的部分，也并不一定是模型本身有升级，而可能是增加了其他的东西。

比如从GPT-3到InstructGPT这一个发展，并不是增加了模型大小，而是基于GPT-3进行了跟人类打标的数据做对齐。

人类指导强化学习并不容易

假如现在给你一个任务，让你发明一套武功叫做太极拳。如果你成功发明出来一个动作跟真实的太极拳一样，就给你加一分。这就是一个强化学习的任务。对于大多数人来说，我们既不是武当张真人，也没有达摩祖师一样的天赋，究我们一生可能一个动作也发明不出来。

如果想让我们能完成这个任务，就需要写个拳谱，或者更进一步，有演示录像。我们参照录像学习，这就是一个人类指导的强化学习的过程。

不过，录像有可能只看到正面，看不到侧面和背面，就算是完美模拟，仍然可能有错误。这时候最好的办法是有老师可以指点一下哪里不对，然后继续练习。

好，现在我们换成当老师的角色，假如我们要教100个学生学习打太极拳，遇到他们每一次出错都要指导纠正，指导一次可能还不够，学生学了后面的还可能忘了前面的。这是不是相当花精力的事情？比如要教100万个学生呢？

我们来看一下Instruct GPT是如何做到的。

有监督的微调

在第一篇的时候，我们已经粗略的看了一眼Instruct GPT的步骤图。经历了对于基础知识和编程实战的历练，现在是时候挑战下原理部分了。

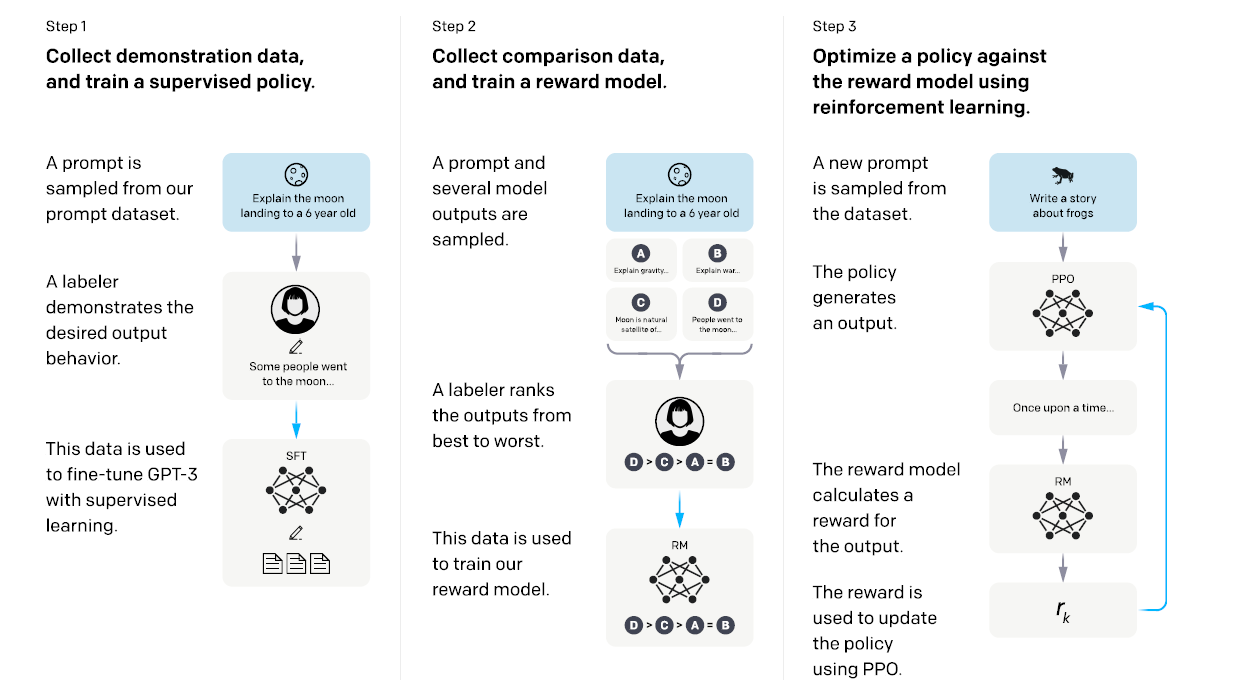
请注意，人类打标的工作是分两部分的：
第一部分是根据问题，由人类写答案。然后用来对大模型进行微调。这一步被称为SFT，有监督的微调。
第二部分是根据模型生成的几个答案，由人类进行排序。人类排序的结果用于训练强化学习的奖励模型。

在准备人类写的答案的时候，OpenAI也是充分动了脑筋的，他们设计了三种情况：

• 纯文本：就是正常平时大家聊家的一问一答的方式。
• few-shot：这其实就是我们学习prompt工程常用到的方式。给出一个指令，然后给出若干组供模型学习的例子。举个例子，指令是英译中，后面给几对英语和对应的中文的例子。
• 预定义的十大类问题：
  • 生成（generation）
  • 开放式问答（open QA）
  • 封闭式问答（closed QA）
  • 头脑风暴（brainstorming）
  • 聊天（chat）
  • 改写（rewriting）
  • 摘要（summarization）
  • 分类（classification）
  • 提取（extraction）
  • 其他（other）

我们来看几个例子。

1. 头脑风暴：列出五个重拾职业热情的想法
2. 封闭式问答：回答以下问题：地球的形状是什么？ A) 圆形 B) 球形 C) 椭圆形 D) 平面
3. 开放式问答：如何对正弦函数求导？
4. 生成：写一个关于一只棕熊去海滩，与一只海豹交朋友，然后返回家的简短故事

人类排序的奖励模型

第二部分，由模型生成，而人来进行排序。模型生成4到9个结果，然后由人类来进行排序。
我们将模型生成的结果记为K，则打标者需要进行$\left(\begin{array}{c}K\\ 2\end{array}\right)$次比较。

我们来看下奖励模型的损失函数：
$$\mathrm{loss}(\theta )=-\frac{1}{\left(\begin{array}{c}K\\ 2\end{array}\right)}{E}_{\left(x,y_w,y_l\right)\sim D}\left[\log \left(\sigma \left(r_{\theta }\left(x,y_w\right)-r_{\theta }\left(x,y_l\right)\right)\right)\right]$$

怕公式的同学不要慌，我来分步解释下，这只是形式化地描述了下，其中并不涉及高深的数学或者机器学习的理论。

其中，x表示输入，$y_w$是排序赢了的输出，$y_l$是输的了。
r是奖励函数，参数为$\theta$。

于是，$r_{\theta }(x,y)$是奖励模型对提示$x$和完成$y$的标量输出。

$\sigma$ 是 sigmoid 函数，将输出值映射到 $(0,1)$ 之间。这表示一个概率，即在给定一对比较时，优选完成 $y_w$ 被选中的概率。

然后取对数，因为对数损失（或者叫交叉熵损失）是优化分类问题的常用方式，它可以直接优化预测的概率。

$\frac{1}{\left(\begin{array}{c}K\\ 2\end{array}\right)}$ 表示归一化因子，用于在不同大小的比较集合之间进行平衡。

$E_{\left(x,y_w,y_l\right)\sim D}$ 表示在数据集 $D$ 上的期望值。$D$ 是包含人类比较的数据集。如果你不理解数学期望的话，这其实就是平均值。

最后，损失函数是所有$\left(\begin{array}{c}K\\ 2\end{array}\right)$个比较的平均对数损失的相反数，取相反数是因为在优化过程中，我们希望最小化损失，而不是最大化损失。
在训练过程中，模型会学会在给定一对完成时，预测人类标签者更可能选择哪个完成。

总结起来一句人话就是：我们希望选择参数$\theta$，使得$r_{\theta }(x,y_w)-r_{\theta }(x,y_l)$尽可能大。也就是让人类选择的结果获取更高的分。

人类指示的强化学习

好，前两步搞明白了，我们讲最后的强化学习。这里使用到了PPO算法。
这里的强化学习部分只是给大家一个概念，用如此小的篇幅能讲明白就见鬼了。大家理解目标在哪里就好，后面我们会用相当的篇幅来详细介绍。

PPO算法

PPO是Proximal Policy Optimization的缩写,是一种策略梯度方法,用于解决强化学习中的策略优化问题。

PPO算法的主要思想是:在策略更新过程中,要确保新旧策略足够接近,以保证学习的稳定性。这是通过引入一个幅度限制来实现的,新策略不能偏离旧策略太多。正如算法名称中“Proximal”所体现的,优化的新策略始终近似于原策略。

比如，发现了门可以进的策略，以后遇见门就优先选择进。

PPO算法的主要步骤是:

1. 定义一个参数化的策略函数${\pi }_{\theta }(a|s)$ ，用神经网络来近似。
2. 用当前的策略 ${\pi }_{\theta }(a|s)$ 与环境交互，收集一批轨迹数据 { s t , a t , r t , s t + 1 } \{s_t,a_t,r_t,s_{t+1}\} {st​,at​,rt​,st+1​} 。
3. 计算每个时间步的优势函数 $A_t$ ，用于评估每个动作的好坏。
4. 定义一个目标函数 $L(\theta )$ ，用于衡量新策略和旧策略的差异，并加入一个惩罚项来防止更新幅度过大。
5. 用梯度下降更新策略参数 $\theta$ ，使目标函数 $L(\theta )$ 最大化。
6. 重复上述步骤，直到策略收敛或达到预设的迭代次数。

PPO算法的主要优点是稳定性高、样本利用率高。相比A2C、ACKTR等方法,PPO可以更快、更稳定地找到较优策略,这使其适合处理许多在线和离线强化学习问题。

回到我们的微调中来，我们构建一个赌博环境，它会呈现一个随机的客户提示，并期望对该提示做出回应。根据提示和回应，它会通过奖励模型生成一个奖励，并结束该回合。此外，我们在每个令牌上添加了来自SFT模型的逐令牌KL惩罚，以减轻对奖励模型的过度优化。价值函数从RM进行初始化。我们将这些模型称为“PPO”。

KL散度

下面还得先补充一个概念，KL散度。

假设你有两个食谱，一个是你跟你妈学的，另一个是你在网上找到的。你按照这两个食谱分别做了两个菜，然后你想知道这两个菜有多相似。你可能会看看它们的颜色、形状、味道等等，然后给出一个"相似度"的评分。这个评分就是KL散度。如果这两个菜完全一致，那么KL散度就是0。如果不一样，那么就是一个大于0的数，差异越大，KL散度的数值越大。

KL散度(KL divergence)是信息论中的一个重要概念, 全名是Kullback-Leibler divergence。它是用来度量两个概率分布之间差异的一种方法。

上面的解释其实还不够说明KL散度的信息论上的含义。

假设你是一个男生，高考报志愿想去一个女生多的专业。你在网上查，某学校的英语专业的男生与女生的比例是1：9。于是兴冲冲报了这个专业。结果当你入学了之后发现，这个专业竟然一个女生都没有，你是不是会特别惊讶？

这个"惊讶度"，就是KL散度要衡量的东西。

从信息论的角度来看，如果你在入学前查到是1：9，入学后发现真是1：9，那么你就没有获得新的信息。但是你发现是10：0，说明你获得了巨大的信息量。

如果你入学后发现，没有1：9那么夸张，但是也达到了3：7，女多男少的情况是真的。你就不会特别惊讶。这时候你获得的信息量比较小,KL散度也比较小。

所以简单地说,KL散度衡量从一个概率分布转到另一个分布,你需要获得多少新的信息,或者另一个分布会给你带来多大的惊讶。如果两个分布很接近,转变不需要新的信息,KL散度很小。如果两个分布很不同,转变需要很多新的信息来减少惊讶,KL散度就比较大。

故事听完了，我们上公式 ^_

KL散度的定义如下:对于两个概率分布P和Q,P的KL散度相对于Q是:

$$KL(P||Q)=\sum _{x}P(x)\log \frac{P(x)}{Q(x)}$$

它有以下几个重要性质:

1. KL散度是非对称的,即$KL(P||Q)\ne KL(Q||P)$。它度量的是$P$相对于$Q$的信息量。

2. KL散度总是非负的,$KL(P||Q)\ge 0$。只有当P和Q完全相同时,$KL(P||Q)=0$。

3. KL散度衡量的是两个分布的差异,而不是距离。它表达的是$P$相对于$Q$丢失或获得的信息量。

4. KL散度并不满足三角不等式。

KL散度有许多应用,主要用于量化概率分布之间的差异,或者作为损失函数的一部分。例如:

• 机器翻译中,限制神经机器翻译与统计机器翻译的差异。
• 变分推断中,测量后验分布与概率模型的差异,并最小化。
• 评估生成模型的性能,比如GAN、VAE等。

所以总的来说,KL散度是一个非常有用的工具,用于衡量和控制概率分布之间的差异程度。在许多机器学习模型和算法中有重要应用。

将强化学习和预训练结合起来

我们还尝试将预训练梯度混合到PPO梯度中，以修复在公共NLP数据集上的性能回归。我们将这些模型称为"PPO-ptx"。在RL训练中，我们最大化以下组合目标函数：

$$\begin{array}{rl}\mathrm{objective}(\varphi )=& E_{(x,y)\sim D_{{\pi }_{\varphi }^{\mathrm{RL}}}}\left[r_{\theta }(x,y)-\beta \log \left({\pi }_{\varphi }^{\mathrm{RL}}(y\mid x)/{\pi }^{\mathrm{SFT}}(y\mid x)\right)\right]+\\ & \gamma E_{x\sim D_{\text{pretrain }}}\left[\log \left({\pi }_{\varphi }^{\mathrm{RL}}(x)\right)\right]\end{array}$$

这个公式定义了PPO-ptx模型的优化目标(objective function)。它由两部分组成:

1. 强化学习部分:
   $$E_{(x,y)\sim D_{{\pi }_{\varphi }^{\mathrm{RL}}}}\left[r_{\theta }(x,y)-\beta \log \left({\pi }_{\varphi }^{\mathrm{RL}}(y\mid x)/{\pi }^{\mathrm{SFT}}(y\mid x)\right)\right]$$
   这部分的含义是:在强化学习得到的轨迹分布$D_{{\pi }_{\varphi }^{\mathrm{RL}}}$下,计算每个时间步的奖励$r_{\theta }(x,y)$与KL惩罚$\beta \log \left({\pi }_{\varphi }^{\mathrm{RL}}(y\mid x)/{\pi }^{\mathrm{SFT}}(y\mid x)\right)$,并取均值。KL惩罚的作用是限制强化学习策略与监督学习策略的差别。
   这个项前的系数$\beta$是KL奖励系数，用于控制KL惩罚的强度。

2. 预训练部分:
   $$\gamma E_{x\sim D_{\text{pretrain }}}\left[\log \left({\pi }_{\varphi }^{\mathrm{RL}}(x)\right)\right]$$
   这部分的含义是:在预训练数据分布$D_{\text{pretrain }}$下,计算强化学习策略的对数似然,并与超参数$\gamma$相乘,作为预训练损失加入到总的优化目标中。

所以总的来说,这个优化目标在强化学习的同时,也利用预训练数据继续训练模型,以修复强化学习在一些NLP数据集上的性能问题。$\beta$和$\gamma$是控制KL惩罚项和预训练损失项强度的超参数。

小结

Chatgpt的成功，跟人类对齐的技术功不可没。

比起用越来越多的数据和越来越强大的算力堆更大的模型，人类打标的工作不管从方案设计上，学习技术上，还是执行上，都是一样费时费力且琐碎的事情。

训练好的大模型是一件充满挑战且要耐得住烦的工作。