前言
解决哈希冲突的方法有闭散列和开散列,上篇博客C++实现闭散列已经讲解完了闭散列的实现方式
本篇博客实现开散列/连地址法的哈希表

文章目录
- 前言
- 一. 开散列
- 二. 开散列实现
- (1). 结构
- (2). 插入
- (3). 查找
- (4). 删除
- (5). 析构函数
- 三. 完整代码
- 结束语
一. 开散列
开散列又叫连地址法(开链法),首先对关键码集合使用哈希函数计算哈希地址,具有相同地址的关键码归于同一子集,每一个子集合称为一个桶,各个桶中的元素通过一个单链表链接起来,各个链表的头结点存储在哈希表中
可以看作线性表挂着一个个链表
哈希函数依然使用除留余数法
Hash(key) = key % capacity
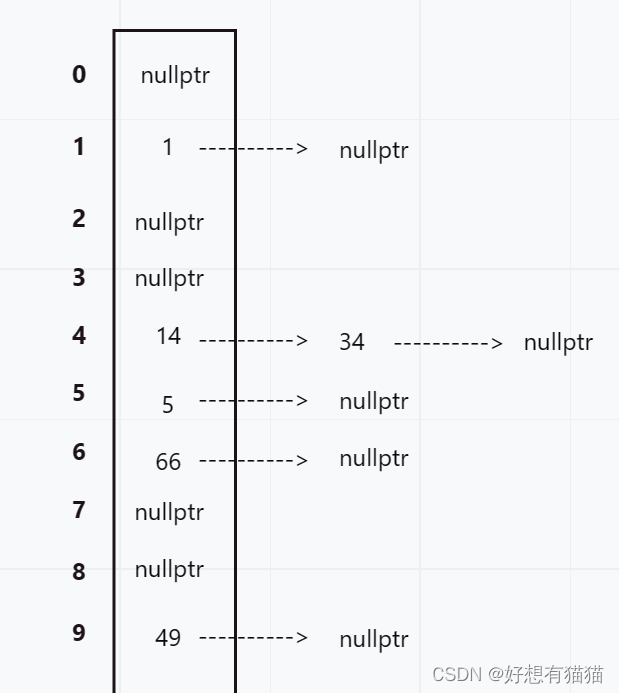
开散列中的每个桶中放的都是发生哈希冲突的元素
二. 开散列实现
我们同样使用除留余数法的哈希函数实现线性表
(1). 结构
这次线性表中存储的不是哈希表结点,而是结点的指针。
//桶结点
template<class K,class V>
struct HashNode
{
pair<K, V>_kv;//值域
HashNode*_next;//指针域
//构造函数
HashNode(const pair<K,V>kv)
:_kv(kv)
,_next(nullptr)
{}
};
template<class K,class V>
class HashBucket
{
typedef HashNode<K, V> Node;
private:
vector<Node*> _tables;//线性表
size_t _n = 0;//大小
};
(2). 插入
插入的逻辑
- 先通过哈希函数,映射到哈希地址
- 使用
头插的方式,链接新结点
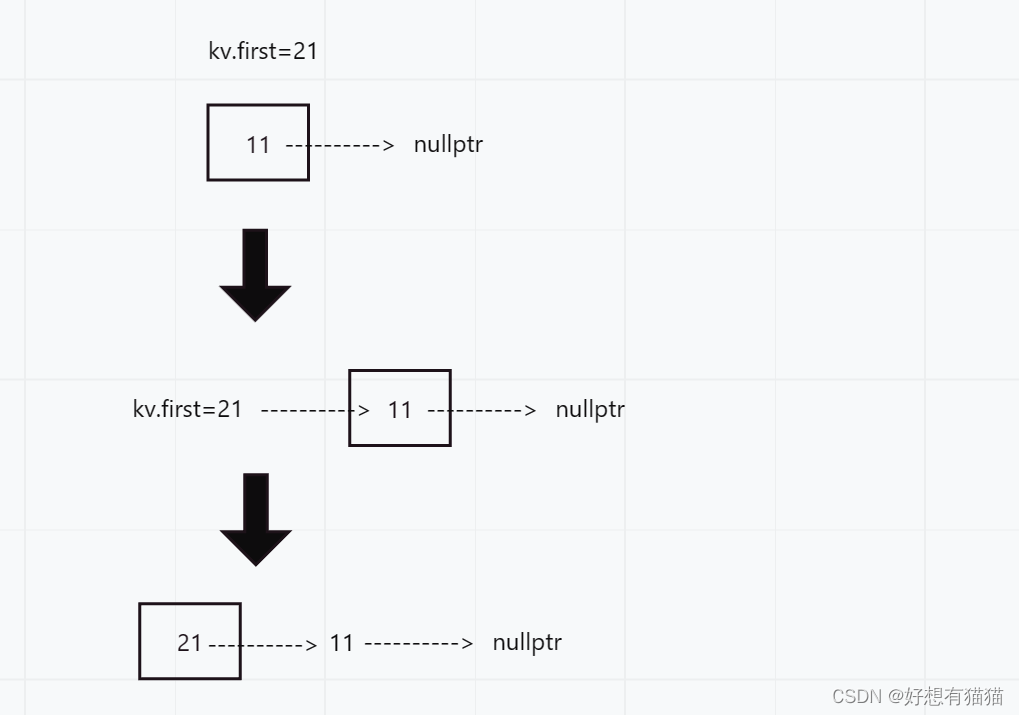
代码如下:
//插入
bool Insert(const pair<K, V>&kv)
{
//寻址
size_t hashi = kv.first%_tables.size();
//头插
Node*newNode = new Node(kv);
newNode->_next = _tables[hashi];
_tables[hashi] = newNode;
_n++;
return true;//插入成功
}
这段代码存在两个问题
- 最开始哈希表的大小为0,那么就会出现
除零异常 - 如果哈希表的容量满了,那么是否需要
扩容
在开散列中,桶的个数是一定的,随着元素的不断插入,每个桶元素的个数不断增多,极端情况下,可能会导致一个桶中链表结点非常多,会影响哈希表的性能,因此在一定条件下需要对哈希表进行扩容。
开散列最好的情况时:每个哈希桶中刚好挂一个结点,再继续插入元素时,每一次都会发生哈希冲突,因此,在元素个数刚好等于桶的个数时,可以对哈希表进行扩容
扩容:我们可以重新开一个vector,然后将原vector的数据取出,重新映射到新vector中,最后交换一下vector即可
代码如下:
//插入
bool Insert(const pair<K, V>&kv)
{
//扩容
if (_n==_tables.size())
{
size_t newSize = _tables.size() == 0 ? 10 : _tables.size() * 2;
vector<Node*>newTables;
newTables.resize(newSize, nullptr);
for (auto &cur : _tables)
{
//将原先的结点直接放到新表中
while (cur)
{
Node*next = cur->_next;
//寻新址
size_t hashi = cur->_kv.first%newSize;
//链接
cur->_next = newTables[hashi];
newTables[hashi] = cur;
cur = next;
}
}
//交换vector
_tables.swap(newTables);
}
//寻址
size_t hashi = kv.first%_tables.size();
//头插
Node*newNode = new Node(kv);
newNode->_next = _tables[hashi];
_tables[hashi] = newNode;
_n++;
return true;//插入成功
}
(3). 查找
查找的逻辑是:
- 根据哈希函数求得哈希地址
- 遍历链表,查找所求值
代码如下:
注意,要判断是否当前为空表,避免出现除零异常
//查找
Node* Find(const K&key)
{
if (_tables.size() == 0)
return false;
//寻址
size_t hashi = key % _tables.size();
Node*cur = _tables[hashi];
while (cur)
{
if (cur->_kv.first == key)
{
return cur;
}
cur = cur->_next;
}
return nullptr;
}
(4). 删除
删除的逻辑如下:
- 根据哈希函数求得哈希地址
- 遍历链表,删除结点
删除结点有两种情况:1.删除的结点为首结点 2. 删除的结点为中间结点
代码如下:
//删除
bool Erase(const K&key)
{
if (_tables.size() == 0)
return false;
size_t hashi = key % _tables.size();
Node*cur = _tables[hashi];
Node*prev = nullptr;
while (cur)
{
if (cur->_kv.first == key)
{
//说明是第一个节点
if (prev == nullptr)
{
_tables[hashi] = cur->_next;
}
else
{
prev->_next = cur->_next;
}
delete cur;
_n--;
return true;
}
else
{
prev = cur;
cur = cur->_next;
}
}
return false;
}
(5). 析构函数
因为Node结点是我们自己new申请的,所以我们需要在析构函数中,将其释放
代码如下:
//析构函数
~HashBucket()
{
for (auto&cur : _tables)
{
while (cur)
{
Node*next = cur->_next;
delete cur;
cur = next;
}
cur = nullptr;
}
}
其实就是遍历线性表,然后将插入的结点挨个释放。
三. 完整代码
#pragma once
//桶结点
template<class K,class V>
struct HashNode
{
pair<K, V>_kv;//值域
HashNode*_next;//指针域
HashNode(const pair<K,V>kv)
:_kv(kv)
,_next(nullptr)
{}
};
template<class K,class V>
class HashBucket
{
typedef HashNode<K, V> Node;
public:
//析构函数
~HashBucket()
{
for (auto&cur : _tables)
{
while (cur)
{
Node*next = cur->_next;
delete cur;
cur = next;
}
cur = nullptr;
}
}
//插入
bool Insert(const pair<K, V>&kv)
{
if (Find(kv.first))
return false;
//扩容
if (_n==_tables.size())
{
size_t newSize = _tables.size() == 0 ? 10 : _tables.size() * 2;
vector<Node*>newTables;
newTables.resize(newSize, nullptr);
for (auto &cur : _tables)
{
//将原先的结点直接放到新表中
while (cur)
{
Node*next = cur->_next;
//寻新址
size_t hashi = cur->_kv.first%newSize;
//链接
cur->_next = newTables[hashi];
newTables[hashi] = cur;
cur = next;
}
}
//交换vector
_tables.swap(newTables);
}
//寻址
size_t hashi = kv.first%_tables.size();
//头插
Node*newNode = new Node(kv);
newNode->_next = _tables[hashi];
_tables[hashi] = newNode;
_n++;
return true;//插入成功
}
//查找
Node* Find(const K&key)
{
if (_tables.size() == 0)
return false;
//寻址
size_t hashi = key % _tables.size();
Node*cur = _tables[hashi];
while (cur)
{
if (cur->_kv.first == key)
{
return cur;
}
cur = cur->_next;
}
return nullptr;
}
//删除
bool Erase(const K&key)
{
if (_tables.size() == 0)
return false;
size_t hashi = key % _tables.size();
Node*cur = _tables[hashi];
Node*prev = nullptr;
while (cur)
{
if (cur->_kv.first == key)
{
//说明是第一个节点
if (prev == nullptr)
{
_tables[hashi] = cur->_next;
}
else
{
prev->_next = cur->_next;
}
delete cur;
_n--;
return true;
}
else
{
prev = cur;
cur = cur->_next;
}
}
return false;
}
private:
vector<Node*> _tables;//线性表
size_t _n = 0;//大小
};
结束语
本篇内容到此就结束了,感谢你的阅读!
如果有补充或者纠正的地方,欢迎评论区补充,纠错。如果觉得本篇文章对你有所帮助的话,不妨点个赞支持一下博主,拜托啦,这对我真的很重要。